Parallel Lines in Maths are the lines in a plane that never cross or intersect at any point, remaining constantly equidistant from one another. These lines run alongside each other indefinitely without ever meeting, although it is sometimes said they converge at infinity. Essentially, parallel lines are lines that do not intersect.
Parallel lines are non-intersecting lines, and they meet at infinity. Broadly lines can be divided into Parallel Lines, Intersecting Lines, and Perpendicular lines.
In this article, we will learn about parallel lines, their properties, axioms, theorems, and detailed examples.
What are Parallel Lines?
Parallel lines are two or more than two lines that are always parallel to each other, and they lie on the same plane. No matter how long parallel lines are extended, they never meet. Parallel lines and intersecting lines are opposite each other. Parallel Lines are the lines that never meet or have any chance of meeting. In the diagram, parallel lines are shown in two ways, Line A is parallel to Line B, and Line X is parallel to Line Y.
Parallel Lines Definition
Parallel lines are the lines in a plane that never cross or intersect at any point, remaining constantly equidistant from one another
Parallel Lines Symbol
Parallel lines symbol is denoted as || as they never meet each other or intersect each other no matter how long they are extended. So, the symbol used to denote the parallel lines is ||. For instance, if AB is parallel to XY, we write it as AB || XY.
The slope is a measurement to determine the extent line is oriented to an axis. In general, we define slope as the tangent of the angle between the X-axis and a line. If the angle between x-axis and a given line is θ, then
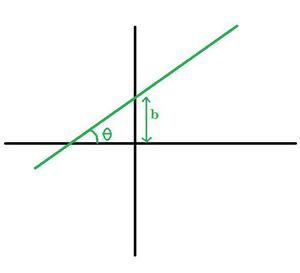Slope of a LineParallel Lines and Transversal
When a line intersects two parallel lines or lines that are not parallel, it is called a transversal. Due to the transversal line, many relations among the pair of angles are created. They can be supplementary or congruent angles.
Suppose the given diagram is creating angles a, b, c, d, and p, q, r, s due to the transversal. These eight separate angles formed by the parallel lines and transversal reflect some properties.
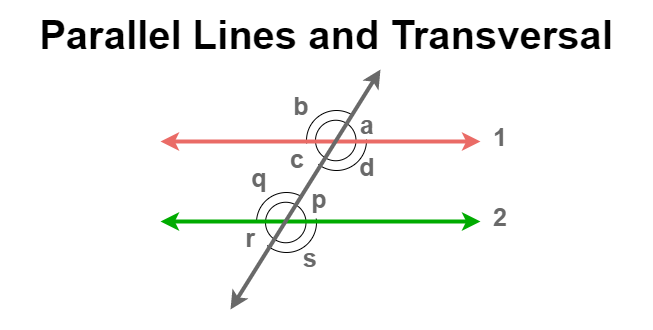Parallel Lines and Transversal
1. For a line with equation y = mx + b, we define:
- m: Slope of the given line
- b: Intercept of the line on the Y-axis.
2. If two points (a, b) and (c, d) on the line are given, then we can find the slope of the line using the formula:
Slope = (b – d) / (a – c)
The equation of the line can be determined by considering a point (x, y) on the line. Since we can also find the slope in terms of x and y, we can write
Slope = (y – d) / (x – c)
Equating this with the actual value of the slope, we can derive the equation for the given line as,
(y – d) / (x – c) = (b – d) / (a – c)
3. For a given line ax + by + c = 0, we can write the slope as:
Slope = – a / b
Angles in Parallel Lines
Angles are created due to transversal and parallel lines 1 and 2. Let's take a look at the properties these angles showcase:
- Alternate Interior Angles: Alternate interior angles are created by the transversal on parallel lines, and they are equal in nature. For example, here, ∠c = ∠p and ∠d = ∠q. The best way to identify the alternate interior angles is by creating a 'Z' in mind. The angles formed by the Z are the alternate interior angles and are equal to each other.
- Alternate Exterior Angles: Alternate exterior angles are also equal in nature. In the diagram above, the alternate exterior angles are ∠a = ∠r and ∠b = ∠s.
- Consecutive Interior Angles: Consecutive interior angles are also known as co-interior angles. They are the angles formed by the transversal on the inside of parallel lines, and they are supplementary to each other. In the above diagram, ∠d + ∠p = 180° and ∠c + ∠q = 180°.
- Vertically Opposite Angles: Vertically opposite angles are formed when two lines intersect each other. The opposite angles are called vertically opposite angles and are parallel to each other. In the above diagram, ∠a = ∠c, ∠b = ∠d, ∠p = ∠r, ∠q = ∠s.
- Corresponding Angles: Corresponding angles in parallel lines are equal to each other. In the above diagram, ∠a = ∠p, ∠d = ∠s, ∠b = ∠q, and ∠c = ∠r.
Parallel Lines Properties
Below are some of the important properties of parallel lines:
- Two or more lines can be considered parallel if, even on extending the lines, there is no chance that the lines will meet or cut each other (intersect each other).
- Parallel lines have the special property of maintaining the same slope.
- The distance between Parallel lines always remains the same. Note: Here, the lines which are considered to be parallel need not be equal in their length, but a mandatory condition for lines to be considered parallel is the distance between the lines remains the same, even on the extension of the lines.
- Parallel lines are denoted by the Pipe symbol (||). For example: If two lines A and B are parallel to each other. They can be represented to be parallel to each other by A || B.
How Do You Know If Lines Are Parallel?
When two or more parallel lines are cut by a transversal, then the angle made by the transversal with the parallel lines shows some distinct properties:
- Parallel lines, when cut by a transversal, have equal alternate interior angles.
- Parallel lines, when cut by a transversal, have equal alternate exterior angles.
- Parallel lines, when cut by a transversal, have equal corresponding angles.
- Parallel lines, when cut by a transversal, have consecutive interior angles on the same side as supplementary.
Violation of any of the above properties will lead to the lines not being considered Parallel Lines.
Parallel Lines Equation
In the parallel line's equation, the slope of the lines is always the same. The equation for a straight line is in slope-intercept form, that is, y = mx + c, where m is the slope. For parallel lines, m will be the same; however, the intercept is not the same.
For example, y = 3x + 8 and y = 3x + 2 are parallel to each other. Therefore, in the parallel line's equation, the intercept is different and has no points in common, but the slope is the same in order to make the lines parallel to each other.
Parallel Lines Axioms and Theorems
Below are the axioms and theorems of parallel lines:
Corresponding Angle Axiom: Corresponding angles are equal to each other. In corresponding angles axioms, it is said that if the reverse of the property is true, that is, if the reason of the property is true, the assertion must be true as well.
The corresponding angles axiom states that if the corresponding angles are equal, it means that the lines on which the transversal is drawn are parallel to each other.
Theorem 1: If a transversal is drawn on two parallel lines, the vertically opposite angles will be equal. From the figure given below:
To Prove: ∠3 = ∠5, ∠4 = ∠6
Proof: ∠1 = ∠3 and ∠5 = ∠7 (Vertically opposite angles)
∠1 = ∠5 (Corresponding angles)
Therefore, ∠3 = ∠5.
Similarly, ∠4 = ∠6.
The converse of the theorem is also true; that is, if the vertically opposite angles are equal to each other, the lines are parallel in nature.
Theorem 2: If two lines are parallel to each other and are intersected by a transversal, the interior angles' pairs are supplementary to each other.
To prove: ∠4 + ∠5 = 180° and ∠3 + ∠6 = 180°.
Proof: ∠4 = ∠6 (Alternate interior angles)
∠6 + ∠5 = 180° (Linear Pair)
Therefore, ∠4 + ∠5 = 180°
Similarly, ∠3 + ∠6 = 180°.
The converse of the theorem is also true; that is, if the interior angles are supplementary to each other, the lines are parallel in nature.
Parallel Lines are Consistent or Inconsistent
In the context of systems of linear equations, if two lines are parallel, it means they have the same slope but different y-intercepts. When you solve such a system, you'll find that there are either infinitely many solutions (if the lines coincide) or no solution (if the lines are distinct and parallel).
Therefore, parallel lines lead to a consistent system with either infinitely many solutions or no solution.
Inconsistent systems occur when the equations describe lines that do not intersect in the plane (i.e., lines that are parallel but not identical), leading to no solution when solving the system
Parallel Lines Applications in Real-Life
Parallel lines can easily be observed in real-life. One of the best examples of parallel lines is the railway tracks. These tracks are literally parallel lines in real life, as they are supposed to be always parallel to each other to grip the wheels of the train at all costs. Some other real-life examples of parallel lines are the edges of an almirah, scale (ruler), etc.
Summary - Parallel Lines
Parallel lines are lines on a plane that never intersect, remaining equidistant from each other indefinitely and often considered to meet only at infinity. These lines are a fundamental concept in geometry, differentiated from intersecting and perpendicular lines. Key characteristics of parallel lines include their consistent slope and the maintenance of a constant distance between them. When a transversal intersects parallel lines, it generates specific angle relationships, including equal alternate interior and exterior angles, supplementary consecutive interior angles, and equal corresponding angles.
Articles related to Parallel Lines:
Parallel Lines Solved Examples
Example 1: In the given figure, angle CMQ is given as 45. Find the rest of the angles.
Solution:
∠CMQ = 45°.
From vertically opposite angles,
∠PMD = 45°.
From linear pair:
∠PMD + ∠PMC = 180°.
⇒ ∠PMC = 135°.
From linear pair:
∠CMQ + ∠DMQ = 180°
⇒ ∠DMQ = 135°.
From Linear pair:
∠DMQ + ∠DMP = 180°.
⇒ ∠DMP = 135°.
From linear pair:
∠CMP + ∠CMQ = 180°.
⇒ ∠CMP = 135°
Thus, ∠ANP = ∠CMP = 135°. (Corresponding angles)
Thus, ∠BNP = ∠DMQ = 135°. (Corresponding angles)
Example 2: Check if the following lines are parallel.
Solution:
Since the distance between the two lines is continuously decreasing, the lines can't be called parallel lines.
Example 3: Check if the following lines are parallel.
Solution:
Since on extending, the two lines don't meet each other and the distance between the two lines remains the same. So, yes the lines can be called Parallel Lines.
Example 4: Find the value of x and y in the given figure where AB is parallel to CD.
Solution:
In the above figure:
2x + 5y + 3x = 180 (Linear pair)
⇒ 5x + 5y = 180
⇒ x + y = 36
⇒ x + y = 3x (Corresponding angles)\
⇒ 36 = 3x
⇒ x = 12
Now, x + y = 36
⇒ 12 + y = 36
⇒ y = 24
Parallel Lines Practice Problems
Problem 1: Given the lines l1, l2, and l3 with slopes 5, 5, and -2 respectively, determine which lines are parallel to each other.
Problem 2: Line m is parallel to line n, and they are cut by a transversal t. If the measure of one of the alternate interior angles formed is 65∘, find the measure of the corresponding angle on the opposite side of the transversal.
Problem 3: Lines a and b are parallel, and a transversal cuts through them creating an angle of 120∘. What are the measures of the consecutive interior angles on the same side as the given angle?
Problem 4: Given the equation of a line y = 2x+3, find the equation of a line parallel to it that passes through the point (−2, 1).