Corresponding angles are a basic concept in geometry. They occur when a transversal line crosses two other lines, creating pairs of angles that are in matching corners at the intersections.
These angles help us understand relationships between parallel lines and are commonly used in both geometry problems and real-world applications like architecture and engineering. In this article, we will learn about the corresponding angle, along with its definition, theorems, and some examples for better understanding.
What are Corresponding Angles with Examples?
When two lines are intersected by another line (called a transversal line), then four interior and four exterior angles are formed. Each of the angles are related to each other. One such relation is corresponding angles.
When two lines intersect with a transversal line, the angles formed at the point of intersection on the respective corners of the same side of the transversal are called as corresponding angles.
The word "corresponding" itself means something similar or equivalent. Hence, the corresponding angles are the angles formed on the corresponding corners of the same side of the transversal.
Examples
There are a total of four pairs of corresponding angles formed by a transversal line. The corresponding angles are illustrated below:
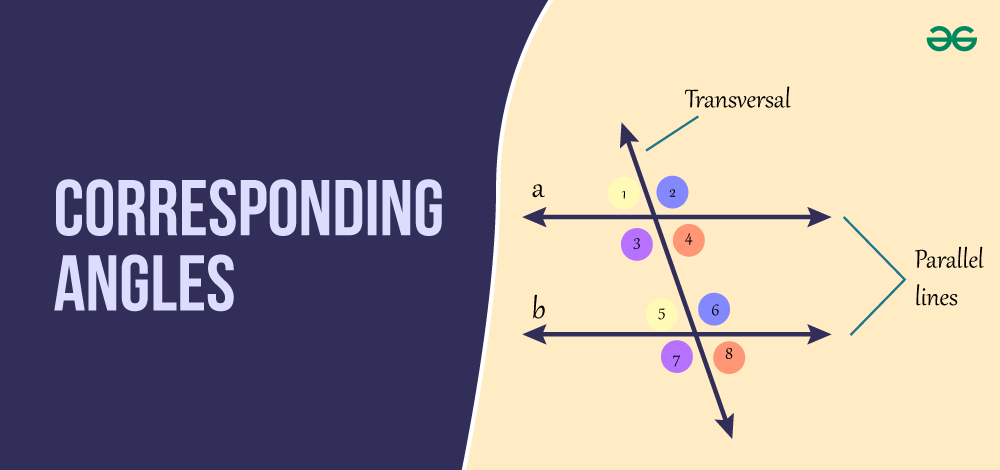
In the above figure, the pair of corresponding angles are:
- ∠1 and ∠5
- ∠2 and ∠6
- ∠3 and ∠7
- ∠4 and ∠8
For example, when two parallel lines are intersected by a transversal, four pairs of corresponding angles are created.
- Congruent corresponding angles: If the two lines are parallel, the corresponding angles are always equal.
- Non-parallel lines: When the transversal intersects two non-parallel lines, the corresponding angles are not equal and have no specific relation.
Necessary Condition of Corresponding Angles
Two angles are said to be a pair of corresponding angles if and only if:
- They are on the same side of the transversal
- One of them is an interior angle and the other is an exterior angle
- They are at different vertex
Learn More,
Types of Corresponding Angles
Corresponding Angles are categorised into two categories namely,
- Corresponding Angles Formed by Parallel Lines and Transversals
- Corresponding Angles Formed by Non-Parallel Lines and Transversals
Let's learn about them in detail.
If a transversal intersects a pair of parallel lines then, the corresponding angles formed are equal to each other. When a transversal intersects a pair of line it results in the formation of eight angles, giving four pairs of corresponding angles. The pair of corresponding angles formed by a transversal are:
- ∠1 and ∠5
- ∠2 and ∠6
- ∠3 and ∠7
- ∠4 and ∠8
In case of parallel lines, the corresponding angles formed are always equal. Therefore:
- ∠1 = ∠5
- ∠2 = ∠6
- ∠3 = ∠7
- ∠4 = ∠8
If a transversal intersects a pair of non-parallel lines then, there is no relation between the formed corresponding angles. The corresponding angles formed in this case are not equal to each other.
 Corresponding Angles by Non Parallel Lines and Transversal
Corresponding Angles by Non Parallel Lines and TransversalCongruency of Corresponding Angles
- When the corresponding angles are formed between two parallel lines and a transversal line, the corresponding angles thus formed are equal and hence congruent.
- When the corresponding angles are formed between two non-parallel lines and a transversal line, the corresponding angles thus formed are unequal and hence not in congruence with each other.
Corresponding Angle Theorem
The corresponding angle theorem states that,
If two parallel lines are intersected by a transversal line, then the corresponding angles thus formed are the same or said to be congruent to each other.
Converse of Corresponding Angle Theorem
The converse of the Corresponding Angle theorem is also true, it states that
If two corresponding angles are equal or congruent to each other, then the lines forming them are parallel to each other.
Steps to Find Corresponding Angles
Step 1: Draw a pair of lines intersected by a transversal and name all the interior and exterior angles as shown in the figure below.

Step 2: Find all the pair of angles which are on the same side of transversal, on different vertex and one angle should be exterior and other should be interior. From the above figure we have the following corresponding angles:
| Pair of Corresponding Angles | Location |
|---|
| ∠1 and ∠5 | Upper Angles on the right side of transversal |
|---|
| ∠2 and ∠6 | Upper Angles on the left side of transversal |
|---|
| ∠3 and ∠7 | Lower Angles on the right side of transversal |
|---|
| ∠4 and ∠8 | Lower Angles on the left side of transversal |
|---|
Corresponding Angles Application
Various applications of corresponding angles are,
- They are used to solve various geometrical problems.
- They are used in Architecture
- They are used in various construction projects, etc.
Also, Check
Solved Examples of Corresponding Angles
Example 1: If two corresponding angles formed by parallel lines are 2x + 1 and 87. Find the value of x.
Solution:
Given 2x + 1 and 87 are corresponding angles formed by parallel lines hence they are equal to each other.
Therefore, 2x + 1 = 87
=> 2x = 87-1
=> 2x = 86
=> x = 86/2
=> x = 43
Hence the value of x is 43.
Example 2: For y = 1, Check whether 3y - 1 and 5 + y are corresponding to each other or not.
Solution:
For y = 1,
Value of 3y - 1
= 3 × 1 - 1
= 3 -1 = 2
and the value of 5 + y
= 5 + 1 = 6
Hence, 3y - 1 ≠ 5 + y
The values of the given two angles are not the same hence these corresponding angles are not formed by parallel lines.
Example 3: For two parallel lines, Find the value of x if 7x - 4 and 2x + 6 are corresponding to each other. Also, find the value of each corresponding angle.
Solution:
Given 7x - 4 and 2x + 6 are corresponding angles formed by parallel lines hence they are equal to each other.
Therefore, 7x - 4 = 2x + 6
Solving the above equation we get,
7x - 4 = 2x + 6
=> 7x - 2x = 6 + 4
=> 5x = 10
=> x = 10/5
=> x = 2
Put x = 2 in 7x - 4 we get
= 7 × 2 - 4
= 14 -4
= 10
Hence the value of x is 2 and the measure of each corresponding angle is 10° .
Example 4: If 5z and 2z + 12 are corresponding angles. For z = 4, check if the lines forming these corresponding angles are parallel or not.
Solution:
For z = 4
Value of 5z = 5 × 4 = 20
and value of 2z + 12 = 2 × 4 + 12 = 8 + 12 = 20
Hence, for z=4, the value of 5z = 2z + 12 and so the given corresponding angles are formed by parallel lines.
Practice Questions on Corresponding Angles
Q1: If x + 1 and 2x -2 are corresponding angles, find the value of each corresponding angle.
Q2: For x = 4, check if 3x + 1 and 2x + 5 are corresponding angles or not.
Q3: The values of two corresponding angles ∠2 = y + 2 and ∠6 = 2y - 7. Find the value of y.
Q4: If two corresponding angles are given by 8z – 10 and 3z + 5. Find the value of each corresponding angle.
Q5: The two corresponding angles are given to be 5x + 5 and 85. Find the value of x.
Similar Reads
Congruent Angles Congruent angles are angles that have equal measure. Thus, all the angles in the geometry that have sam measure are called congruent angles. In this article, we will understand the meaning of congruent angles, their properties, the congruent angles theorem, the vertical angles theorem, the correspon
12 min read
What is Correspondence Analysis? In the era of big data, businesses and researchers are constantly seeking effective methods to analyze and extract meaningful insights from complex datasets. Traditional statistical techniques may not always suffice, especially when dealing with high-dimensional and categorical data. In such scenari
12 min read
Applications of Corresponding Angles in Everyday Life Angles are everywhere around us, shaping our surroundings and influencing how things fit together. One type of angle, called corresponding angles, might sound like something from a math class, but it's actually something we encounter in our daily lives more often than we realize. In this article, we
4 min read
What is Correlation Analysis? Most of the data in the world is interrelated by various factors. Data Science deals with understanding the relationships between different variables. This helps us learn the underlying patterns and connections that can give us valuable insights. "Correlation Analysis" is an important tool used to u
6 min read
Covariance and Correlation Covariance and correlation are the two key concepts in Statistics that help us analyze the relationship between two variables. Covariance measures how two variables change together, indicating whether they move in the same or opposite directions. Relationship between Independent and dependent variab
5 min read