Lines in Geometry- Definition, Types and Examples
Last Updated : 30 Sep, 2024
A line in geometry is a straight path that goes on forever in both directions. It has no thickness and is usually drawn between two points, but it keeps going without stopping. Lines are important for making shapes, measuring distances, and understanding angles. For example, the edge of a ruler can represent a line.
In this article, we will discuss the introduction, definition of Line, and its meaning. We will also understand the different types of Lines and various equations related to Lines. We will also solve various examples and provide practice questions for a better understanding of the concept of this article.
Line in Geometry
Lines serve as the foundational elements of geometry. It plays an important role in understanding mathematical concepts. A line represents an infinitely extended, straight, one-dimensional pathway without endpoints in both directions. Typically, It is represented by a lowercase letter (e.g., 'l') or defined by two points (e.g., 'AB'). Daily life examples of a line can be seen in railway tracks and straight roads.

The credit for introducing the concept of a line goes to Euclid, the esteemed Greek mathematician fondly known as the Father of Geometry. Euclid characterized a line as "a breadthless length”.
A Line is created by a collection of points moving along a straight trajectory but in opposing directions. Without breadth, depth, or curvature, a line keeps moving in a straight path endlessly in opposite directions. An absence of termination characterizes this continuous motion.
Line Segment
A Line Segment is defined as a line with two fixed endpoints. A line segment maintains a constant length, representing the distance between its two endpoints.

Ray
A Ray is defined as a line which has fixed starting point but lacks a defined endpoint. A ray can extend infinitely in a singular direction. Due to the absence of an endpoint, measurement the length of a ray is not applicable. For examples, a sunray or the light emitted from a torch, where the sun or the torch serves as the originating point, and the ray extends indefinitely.

Difference Between Line, Line Segment and Ray
Line, Line Segment and Rays are fundamental for geometrical figure. They sound and look similar but have significant difference between them. Let's learn the difference between Line, Line segment and Rays in tabular form:
Line | Line Segment | Ray |
|---|
A Line is a collection of points that go forever in two opposite directions indefinitely. It is an endless continuous and it has no finite endpoints | Line Segment is a part of the line that can link two fixed or definite endpoints, in which all points exist between these end points. | When a line has a starting point but not a finite end point means end at infinity is called a Ray. |
It is represented with arrows at both ends to show that it extends infinitely in both directions. | It has a definite length and it does not extend infinitely in both the direction. | It represents one start point and an arrow at the other end that means it moves forever in one direction. |
It is represented by ↔. | It is represented by a bar ‘―’ on the top of two endpoints. | It is represented by →. |
Types of Lines
In geometry, various types of Lines exist, each with distinct characteristics. Let’s understand these Lines:
Straight Line
A Straight Line is a group of collinear points without any curves, extending infinitely in opposite directions.
Curved Line
Curved Line is a group of collinear points with curvature or bends in its configuration. For example, curve line can be seen in the meandering course of a river.
Oblique or Slanting Line
Oblique or Slanting Lines are lines drawn in a slanting position, forming angles other than 0, 90, 180, 270, or 360 degrees with horizontal or vertical lines.
Horizontal Line
Horizontal Line is a straight line extending from left to right or vice versa. It is also known as a sleeping line. Horizontal line can be seen lines on notebook paper, and table edges.
Vertical Line
Vertical Line extends from top to bottom or bottom to top, known as a standing line. Anything forming a right angle with the horizontal line is considered vertical. Vertical line can be observed in the skyline or the edge of a book.
Parallel Line
Parallel Lines are found in striped patterns or fence posts, are two lines on the same plane maintaining equal and constant distance without intersecting.
Intersecting Line
Lines on the same plane intersecting at a specific point are known as Intersecting Lines. The image added below shows the parallel and intersecting lines, here l and m are parallel lines, and p and q are intersecting lines.

Transversal Line
Transversal Line intersects two or more parallel or non-parallel lines at a defined point. Transversal line and parallel line should be lie on the same plane.
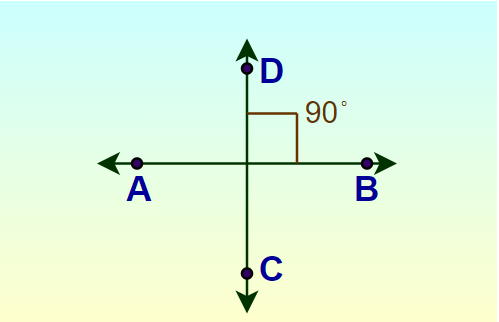
Perpendicular Line
Perpendicular Lines occur when two lines intersect each other on the same plane, forming a right angle (90°) at the point of intersection. The perpendicular lines AB and CD are shown in the image added below.
Few more types of Lines
- Secant Line: A line is considered a secant line to a circle when it intersects the circle precisely at two points.
- Skew Line: Skew Lines are lines lacking intersections with each other but unevenly spaced, distinct from parallel lines.
- Tangent Line: Tangent Lines are lines that touch the curve at only one point.
- Diagonal Line: Diagonal Line is a straight line that is set at an angle and connects the opposite corner of any shape.
- Contour Line: Contour Line defines the outer edges of any shape. For example- the outline of a mountain range.
- Dotted Line: Dotted Line are used in design to indicate a path or connection. For example- Dotted lines on a map.
General Equation of Line
General Equation of a Line in two variables with a degree of one is expressed as Ax + By + C = 0, where A and B cannot both be zero; and A, B, and C are real numbers.
This representation is commonly known as a linear equation in two variables.
For example: Consider the example 4x + 9y - 6 = 0, where A = 4, B = 9, and C = -6.
This equation is a specific example of the general form of line, showing the coefficients A, B, and C associated with the line.
There is various ways to show the equation of line. These forms are:
In Point-slope form, the line is passing through a point (x0,y0) with a slope of m then the equation is expressed as:
(y - y0) = m(x - x0)
In Two-point form, the line passes through two points say (x1,y1) and (x2,y2) then the equation of line is expressed as
y - y1 = {(y2-y1)/(x2-x1)}(x - x1)
In Slope-Intercept form, a line with a slope of m intersecting the y-axis at a distance of a point (0, c), that distance is known as the y-intercept of a line.
Equation of the line will be given as
y = mx+c
When a line intersects the x-axis at (a, 0) and the y-axis at (0, b), the equation can be derived using the two-point form,
y - y1 = {(y2-y1)/(x2-x1)}(x - x1)
By putting the value, we get
y-0 = {(b-0)/(0-a)}(x-a)
By rearranging the equation, we get
x/a+y/b = 1
This expression is recognized as the intercept form.
Also, Read
Real-World Applications of Lines in Geometry
Lines in geometry are not just abstract concepts; they have many real-world applications. In architecture and engineering, lines are used to design buildings, bridges, and other structures. For example, architects use parallel and perpendicular lines to create strong and balanced structures. Similarly, in art, lines are
Solved Examples on Line
Example 1: Determine the equation of the line for x-axis and y-axis.
Solution:
The x-axis is represented by the equation y=0, while the y-axis is denoted by x=0.
Example 2: Determine the equation of the line with a slope of 6 passing through the point (9,3).
Solution:
We have the slope m=6 and passing coordinates (x0,y0) = (9,3)
Now, by using
(y-y0) = m(x-x0)
(y-3) = 6 (x-9)
y-3 = 6x-54
6x-y = 51
y = 6x-51
Example 3: Determine the equation of a line when passing through (3,2) and (-4,8).
Solution:
Here, the Line is passing through coordinates (x1, x2) = (3,2) and (y1, y2) = (-4,8)
Now,
y-y1 = {(y2-y1)/(x2-x1)}(x-x1)
y-2 = {(8-2)/(-4-3)}/(x-3)
y-2= {6/-7}/(x-3)
-7y+14 = 6x-18
6x+7y-32=0
Example 4: Determine the y-intercept of a line 2x+5y=20.
Solution:
The given equation is 2x+5y=20
Change this equation in this form
x/a+y/b =1.
Now,
2x+5y = 20
2x/20 + 5y/20 = 1
x/10 + y/4 = 1
Hence, the y-intercept is 4.
Example 5: Determine the equation of a line passing through (1,4) and m=6.
Solution:
We have the slope m=6 and passing coordinates (x0,y0) = (1,4)
Now, by using
(y-y0) = m(x-x0)
y-4 = 6(x-1)
y-4 = 6x-6
y = 6x-2
Practice Questions on a Line
Q1. Determine the slope for the equation y = 2x + 3.
Q2. Find the point where the line 3x + 6y = 15 intersects the y-axis, means y-intercept.
Q3. Write the equation of a line when passing through the points (3,9) and (-2,4).
Q4. Find the equation of a line passing through the point (2,8) with a given slope of 4.
Q5. Determine the point where the line given by the equation y = 2x + 3 intersects the x-axis, means x-intercept.
Similar Reads
Geometry Geometry is a branch of mathematics that studies the properties, measurements, and relationships of points, lines, angles, surfaces, and solids. From basic lines and angles to complex structures, it helps us understand the world around us.Geometry for Students and BeginnersThis section covers key br
2 min read
Lines and Angles
Lines in Geometry- Definition, Types and ExamplesA line in geometry is a straight path that goes on forever in both directions. It has no thickness and is usually drawn between two points, but it keeps going without stopping. Lines are important for making shapes, measuring distances, and understanding angles. For example, the edge of a ruler can
9 min read
Difference between a Line and a RayThe word 'geometry' is the English equivalent of the Greek word 'geometron'. 'Geo' means Earth and 'Metron' means Measure. Even today geometric ideas are reflected in many forms of art, measurement, textile, designing, engineering, etc. All objects have different sizes. For example, the geometry of
3 min read
Angles | Definition, Types and ExamplesIn geometry, an angle is a figure that is formed by two intersecting rays or line segments that share a common endpoint. The word “angle†is derived from the Latin word “angulusâ€, which means “cornerâ€. The two lines joined together are called the arms of the angle and the measure of the opening betw
13 min read
Types of AnglesTypes of Angles: An angle is a geometric figure formed by two rays meeting at a common endpoint. It is measured in degrees or radians. It deals with the relationship of points, lines, angles, and shapes in space. Understanding different types of angles is crucial for solving theoretical problems in
10 min read
2D Geometry
Polygons
Polygon Formula - Definition, Symbol, ExamplesPolygons are closed two-dimensional shapes made with three or more lines, where each line intersects at vertices. Polygons can have various numbers of sides, such as three (triangles), four (quadrilaterals), and more. In this article, we will learn about the polygon definition, the characteristics o
7 min read
Types of PolygonsTypes of Polygons classify all polygons based on various parameters. As we know, a polygon is a closed figure consisting only of straight lines on its edges. In other words, polygons are closed figures made up of more than 2 line segments on a 2-dimensional plane. The word Polygon is made up of two
9 min read
Exterior Angles of a PolygonPolygon is a closed, connected shape made of straight lines. It may be a flat or a plane figure spanned across two-dimensions. A polygon is an enclosed figure that can have more than 3 sides. The lines forming the polygon are known as the edges or sides and the points where they meet are known as ve
6 min read
Triangles
Triangles in GeometryA triangle is a polygon with three sides (edges), three vertices (corners), and three angles. It is the simplest polygon in geometry, and the sum of its interior angles is always 180°. A triangle is formed by three line segments (edges) that intersect at three vertices, creating a two-dimensional re
13 min read
Types of TrianglesA triangle is a polygon with three sides and three angles. It is one of the simplest and most fundamental shapes in geometry. A triangle has these key Properties:Sides: A triangle has three sides, which can have different lengths.Angles: A triangle has three interior angles, and the sum of these ang
5 min read
Angle Sum Property of a TriangleAngle Sum Property of a Triangle is the special property of a triangle that is used to find the value of an unknown angle in the triangle. It is the most widely used property of a triangle and according to this property, "Sum of All the Angles of a Triangle is equal to 180º." Angle Sum Property of a
8 min read
Area of a Triangle | Formula and ExamplesThe area of the triangle is a basic geometric concept that calculates the measure of the space enclosed by the three sides of the triangle. The formulas to find the area of a triangle include the base-height formula, Heron's formula, and trigonometric methods.The area of triangle is generally calcul
6 min read
Theorem - Angle opposite to equal sides of an isosceles triangle are equal | Class 9 MathsIn geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Exampl
4 min read
GRE Geometry | TrianglesTriangle is one of the basic 2-D shapes in geometry. It consists of three angles, three side and three vertices, e.g., On the basis of measurement of sides and angles there different types of triangle listed below: 1. Equilateral triangle: All edges are equal, all angles are also equal to 60°, e.g.,
3 min read
Triangle Inequality Theorem, Proof & ApplicationsTriangle Inequality Theorem is the relation between the sides and angles of triangles which helps us understand the properties and solutions related to triangles. Triangles are the most fundamental geometric shape as we can't make any closed shape with two or one side. Triangles consist of three sid
8 min read
Congruence of Triangles |SSS, SAS, ASA, and RHS RulesCongruence of triangles is a concept in geometry which is used to compare different shapes. It is the condition between two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each othe
9 min read
Mid Point TheoremThe Midpoint Theorem is a fundamental concept in geometry that simplifies solving problems involving triangles. It establishes a relationship between the midpoints of two sides of a triangle and the third side. This theorem is especially useful in coordinate geometry and in proving other mathematica
6 min read
X and Y Intercept FormulaX and Y Intercept Formula as the name suggests, is the formula to calculate the intercept of a given straight line. An intercept is defined as the point at which the line or curve intersects the graph's axis. The intercept of a line is the point at which it intersects the x-axis or the y-axis. When
9 min read
Basic Proportionality Theorem (BPT) Class 10 | Proof and ExamplesBasic Proportionality Theorem: Thales theorem is one of the most fundamental theorems in geometry that relates the parts of the length of sides of triangles. The other name of the Thales theorem is the Basic Proportionality Theorem or BPT. BPT states that if a line is parallel to a side of a triangl
8 min read
Criteria for Similarity of TrianglesThings are often referred similar when the physical structure or patterns they show have similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In
9 min read
Pythagoras Theorem | Formula, Proof and ExamplesPythagoras Theorem explains the relationship between the three sides of a right-angled triangle and helps us find the length of a missing side if the other two sides are known. It is also known as the Pythagorean theorem. It states that in a right-angled triangle, the square of the hypotenuse is equ
9 min read
Quadrilateral
Types of Quadrilaterals and Their PropertiesA quadrilateral is a polygon with four sides, four vertices, and four angles. There are several types of quadrilaterals, each with its own properties and characteristics. All different types of quadrilaterals have very distinct shapes and properties which help us identify these quadrilaterals. Types
12 min read
Angle Sum Property of a QuadrilateralAngle Sum Property of a Quadrilateral: Quadrilaterals are encountered everywhere in life, every square rectangle, any shape with four sides is a quadrilateral. We know, three non-collinear points make a triangle. Similarly, four non-collinear points take up a shape that is called a quadrilateral. It
9 min read
Parallelogram | Properties, Formulas, Types, and TheoremA parallelogram is a two-dimensional geometrical shape whose opposite sides are equal in length and are parallel. The opposite angles of a parallelogram are equal in measure and the Sum of adjacent angles of a parallelogram is equal to 180 degrees.A parallelogram is a four-sided polygon (quadrilater
10 min read
Rhombus: Definition, Properties, Formula and ExamplesA rhombus is a type of quadrilateral with the following additional properties. All four sides are of equal length and opposite sides parallel. The opposite angles are equal, and the diagonals bisect each other at right angles. A rhombus is a special case of a parallelogram, and if all its angles are
6 min read
Square in Maths - Area, Perimeter, Examples & ApplicationsA square is a type of quadrilateral where all four sides are of equal length and each interior angle measures 90°. It has two pairs of parallel sides, with opposite sides being parallel. The diagonals of a square are equal in length and bisect each other at right angles.Squares are used in various f
5 min read
Rectangle | Definition, Properties, FormulasA rectangle is a quadrilateral with four sides and following properties. All four angles are right angles (90°). The opposite sides of a rectangle are equal in length and parallel to each other.A rectangle is a two-dimensional flat shape. Illustration of a Rectangle Here, sides AB and CD are equal a
7 min read
Trapezium: Types | Formulas |Properties & ExamplesA Trapezium or Trapezoid is a quadrilateral (shape with 4 sides) with exactly one pair of opposite sides parallel to each other. The term "trapezium" comes from the Greek word "trapeze," meaning "table." It is a two-dimensional shape with four sides and four vertices.In the figure below, a and b are
8 min read
Kite - QuadrilateralsA Kite is a special type of quadrilateral that is easily recognizable by its unique shape, resembling the traditional toy flown on a string. In geometry, a kite has two pairs of adjacent sides that are of equal length. This distinctive feature sets it apart from other quadrilaterals like squares, re
8 min read
Area of Parallelogram | Definition, Formulas & ExamplesA parallelogram is a four-sided polygon (quadrilateral) where opposite sides are parallel and equal in length. In a parallelogram, the opposite angles are also equal, and the diagonals bisect each other (they cut each other into two equal parts).The area of a Parallelogram is the space or the region
8 min read
Euclid’s Geometry
Circle
Circles in MathsA circle is a two-dimensional shape where all points on the circumference are the same distance from the center.A circle consists of all points in a plane that are equidistant (at the same distance) from a fixed point called the centre. The distance from the centre to any point on the circle is call
10 min read
Circumference of Circle - Definition, Perimeter Formula, and ExamplesThe circumference of a circle is the distance around its boundary, much like the perimeter of any other shape. It is a key concept in geometry, particularly when dealing with circles in real-world applications such as measuring the distance traveled by wheels or calculating the boundary of round obj
7 min read
Area of a Circle: Formula, Derivation, ExamplesThe area of a Circle is the measure of the two-dimensional space enclosed within its boundaries. It is mostly calculated by the size of the circle's radius which is the distance from the center of the circle to any point on its edge. The area of a circle is proportional to the radius of the circle.
10 min read
Area of a Circular SectorA circular sector or circle sector is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. Let's look at this figure and try to figure out the sector: source: Wikipedia ( https://goo.gl/mWijn2 ) In this fig
4 min read
Segment of a CircleSegment of a Circle is one of the important parts of the circle other than the sector. As we know, the circle is a 2-D shape in which points are equidistant from the point and the line connecting the two points lying on the circumference of the circle is called the chord of the circle. The area form
7 min read
Circle TheoremsCircle is a collection of points that are at a fixed distance from a particular point. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle. We come across many objects in real life which are round in shape. For example, wheels of vehicles, ban
5 min read
Tangent to a CircleTangent in Circles are the line segments that touch the given curve only at one particular point. Tangent is a Greek word meaning "To Touch". For a circle, we can say that the line which touches the circle from the outside at one single point on the circumference is called the tangent of the circle.
10 min read
Theorem - The tangent at any point of a circle is perpendicular to the radius through the point of contactA tangent is a straight line drawn from an external point that touches a circle at exactly one point on the circumference of the circle. There can be an infinite number of tangents to a circle. These tangents follow certain properties that can be used as identities to perform mathematical computatio
3 min read
Number of Tangents from a Point on a CircleA circle is a collection of all the points in a plane that are at a constant distance from a particular point. This distance is called the radius of the circle and the fixed point is called the centre. Â A straight line and a circle can co-exist in three ways, one can be a straight line with no inter
11 min read
Theorem - The lengths of tangents drawn from an external point to a circle are equal - Circles | Class 10 MathsTangent is a straight line drawn from an external point that touches a circle at exactly one point on the circumference of the circle. There can be an infinite number of tangents of a circle. These tangents follow certain properties that can be used as identities to perform mathematical computations
5 min read
Equation of a CircleA circle is a geometric shape described as the set of all points in a plane that are equidistant from a fixed point called the center. The distance from the center to any point on the circle is called the radius. Some key components of the circle are:Center: The fixed point in the middle of the circ
14 min read
What is Cyclic QuadrilateralCyclic Quadrilateral is a special type of quadrilateral in which all the vertices of the quadrilateral lie on the circumference of a circle. In other words, if you draw a quadrilateral and then find a circle that passes through all four vertices of that quadrilateral, then that quadrilateral is call
9 min read
The sum of opposite angles of a cyclic quadrilateral is 180° | Class 9 Maths TheoremIn Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the cir
6 min read
3D Geometry
Visualizing Solid ShapesVisualizing Solid Shapes: Any plane or any shape has two measurements length and width, which is why it is called a two-dimensional(2D) object. Circles, squares, triangles, rectangles, trapeziums, etc. are 2-D shapes. If an object has length, width, and breadth then it is a three-dimensional object(
8 min read
Polyhedron | Meaning, Shapes, Formula, and ExamplesA polyhedron is a 3D solid made up of flat polygonal faces, with edges meeting at vertices. Each face is a polygon, and the edges connect the faces at their vertices. Examples include cubes, prisms, and pyramids. Shapes like cones and spheres are not polyhedrons because they lack polygonal faces.Pol
6 min read
Difference between 2D and 3D Shapes2D shapes are flat like pictures on paper, with just length and breadth but not depth. On the other hand, 3D shapes are like real objects you can touch, with length, breadth, and depth. They take up space, like a toy that you can hold. Examples of 2D shapes include squares and circles. Cubes, sphere
3 min read
Lines
Equation of a Straight Line | Forms, Examples and Practice QuestionsThe equation of a line describes the relationship between the x-coordinates and y-coordinates of all points that lie on the line. It provides a way to mathematically represent that straight path.In general, the equation of a straight line can be written in several forms, depending on the information
10 min read
Slope of a LineSlope of a Line is the measure of the steepness of a line, a surface, or a curve, whichever is the point of consideration. The slope of a Line is a fundamental concept in the stream of calculus or coordinate geometry, or we can say the slope of a line is fundamental to the complete mathematics subje
12 min read
Angle between a Pair of LinesGiven two integers M1 and M2 representing the slope of two lines intersecting at a point, the task is to find the angle between these two lines. Examples: Input: M1 = 1.75, M2 = 0.27Output: 45.1455 degrees Input: M1 = 0.5, M2 = 1.75Output: 33.6901 degrees Approach: If ? is the angle between the two
4 min read
Slope Intercept FormThe slope-intercept formula is one of the formulas used to find the equation of a line. The slope-intercept formula of a line with slope m and y-intercept b is, y = mx + b. Here (x, y) is any point on the line. It represents a straight line that cuts both axes. Slope intercept form of the equation i
9 min read
Point Slope Form Formula of a LineIn geometry, there are several forms to represent the equation of a straight line on the two-dimensional coordinate plane. There can be infinite lines with a given slope, but when we specify that the line passes through a given point then we get a unique straight line. Different forms of equations o
6 min read
Writing Slope-Intercept EquationsStraight-line equations, also known as "linear" equations, have simple variable expressions with no exponents and graph as straight lines. A straight-line equation is one that has only two variables: x and y, rather than variables like y2 or √x. Because it contains information about these two proper
10 min read
Slope of perpendicular to lineYou are given the slope of one line (m1) and you have to find the slope of another line which is perpendicular to the given line. Examples: Input : 5 Output : Slope of perpendicular line is : -0.20 Input : 4 Output : Slope of perpendicular line is : -0.25 Suppose we are given two perpendicular line
3 min read
What is the Point of Intersection of Two Lines Formula?If we consider two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, the point of intersection of these two lines is given by the formula:(x, y) = \left( \frac{b_1 c_2 \ - \ b_2 c_1}{a_1 b_2 \ - \ a_2 b_1}, \frac{c_1 a_2 \ - \ c_2 a_1}{a_1 b_2 \ - \ a_2 b_1} \right),The given illustration shows the i
5 min read
Slope of the line parallel to the line with the given slopeGiven an integer m which is the slope of a line, the task is to find the slope of the line which is parallel to the given line. Examples: Input: m = 2 Output: 2 Input: m = -3 Output: -3 Approach: Let P and Q be two parallel lines with equations y = m1x + b1, and y = m2x + b2 respectively. Here m1 an
3 min read
Minimum distance from a point to the line segment using VectorsGiven the coordinates of two endpoints A(x1, y1), B(x2, y2) of the line segment and coordinates of a point E(x, y); the task is to find the minimum distance from the point to line segment formed with the given coordinates.Note that both the ends of a line can go to infinity i.e. a line has no ending
10 min read
Distance between two parallel linesGiven are two parallel straight lines with slope m, and different y-intercepts b1 & b2.The task is to find the distance between these two parallel lines.Examples: Input: m = 2, b1 = 4, b2 = 3 Output: 0.333333 Input: m = -4, b1 = 11, b2 = 23 Output: 0.8 Approach: Let PQ and RS be the parallel lin
4 min read
Equation of a straight line passing through a point and making a given angle with a given lineGiven four integers a, b, c representing coefficients of a straight line with equation (ax + by + c = 0), the task is to find the equations of the two straight lines passing through a given point (x1, y1) and making an angle ? with the given straight line. Examples: Input: a = 2, b = 3, c = -7, x1 =
15+ min read