У цьому модулі ви ознайомитеся з поняттями лінійної регресії.
Лінійна регресія – це статистичний метод, який використовується для пошуку взаємозв’язку між змінними. У контексті машинного навчання лінійна регресія знаходить зв’язок між ознаками й міткою.
Припустімо, що ми хочемо передбачити паливну економічність у милях на галон для автомобілів, виходячи з того, наскільки вони важкі, і маємо такий набір даних:
| Фунти в тисячах (ознака) | Милі на галон (мітка) |
|---|---|
| 3,5 | 18 |
| 3,69 | 15 |
| 3,44 | 18 |
| 3,43 | 16 |
| 4,34 | 15 |
| 4,42 | 14 |
| 2,37 | 24 |
Ось що ми отримаємо, якщо побудуємо графік із точками на основі цих даних:

Рисунок 1. Вага автомобіля (у фунтах) порівняно з показником миль на галон. Коли автомобіль стає важчим, його показник миль на галон, як правило, зменшується.
Можна створити власну модель, провівши лінію найкращої відповідності між точками.

Рисунок 2. Лінія найкращої відповідності, проведена через дані з попереднього рисунка.
Рівняння лінійної регресії
Модель, виражена алгебраїчним рівнянням, буде такою: $ y = mx + b $, де:
- $ y $ – милі на галон (це величина, яку потрібно спрогнозувати);
- $ m $ – нахил лінії;
- $ x $ – фунт (наше вхідне значення);
- $ b $ – точка перетину з віссю "y".
У машинному навчанні рівняння моделі лінійної регресії записуються так:
де:
- $ y' $ – прогнозована мітка (вихідні дані);
- $ b $ – зсув моделі (зсув – це те саме поняття, що й точка перетину з віссю "y" в алгебраїчному рівнянні для прямої; у машинному навчанні зсув іноді позначають як $ w_0 $; це параметр моделі, що обчислюється під час навчання);
- $ w_1 $ – вага ознаки (вага – це те саме поняття, що й нахил $ m $ в алгебраїчному рівнянні для прямої; це параметр моделі, що обчислюється під час навчання);
- $ x_1 $ – це ознака (вхідні дані).
Під час навчання розраховуються вага й зсув, що будуть найкращими для моделі.
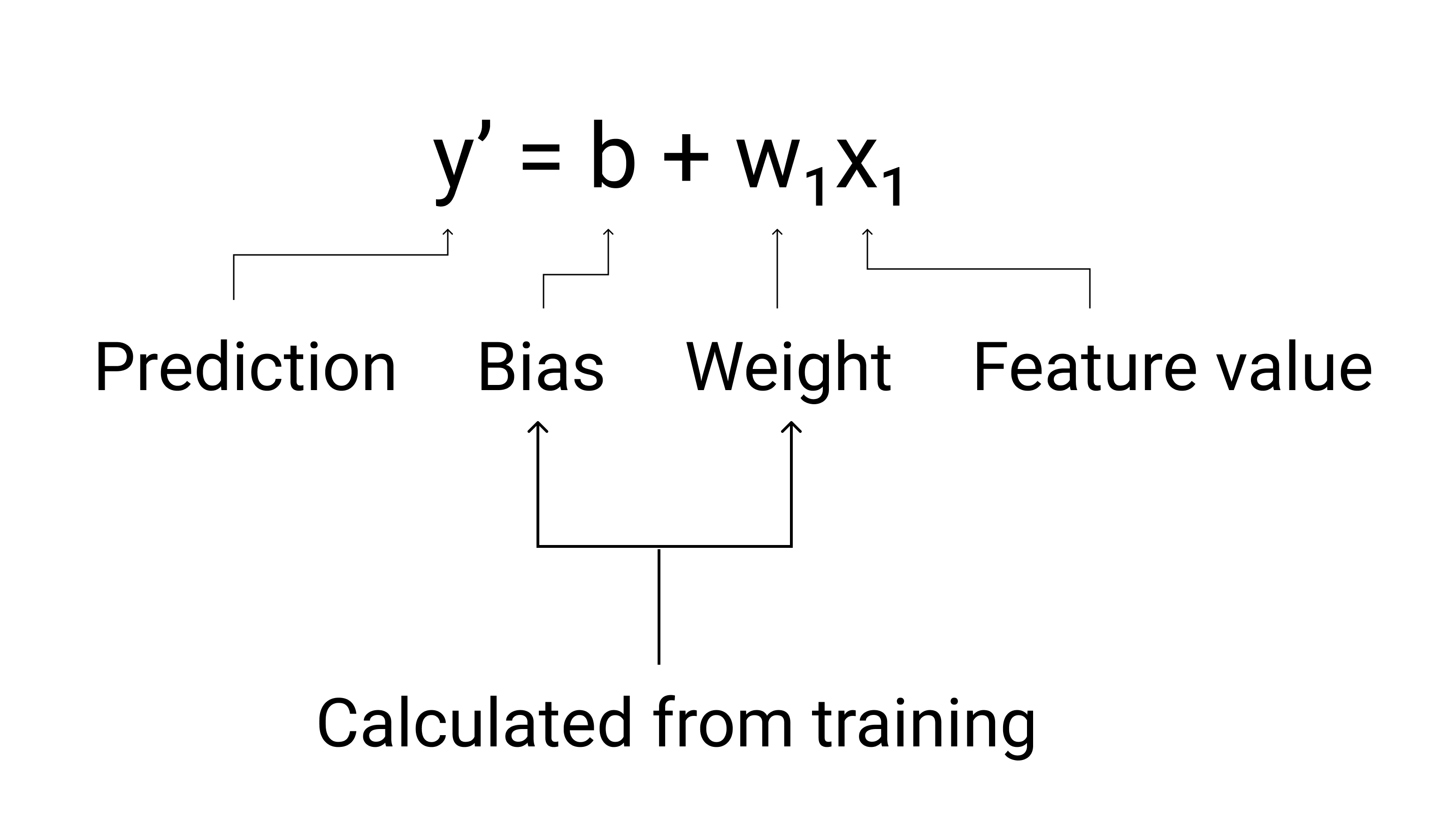
Рисунок 3. Математичне представлення лінійної моделі.
У цьому прикладі ми обчислимо вагу й зсув на основі проведеної лінії. Показник зсуву дорівнює 30 (у точці перетину лінії з віссю "y"), а вага становить –3,6 (нахил лінії). Модель матиме вигляд y' = 30 + (–3,6)(x_1), і на її основі можна буде робити прогнози. Наприклад, згідно із цією моделлю, автомобіль вагою 4000 фунтів матиме прогнозовану паливну економічність 15,6 милі на галон.

Рисунок 4. Згідно із цією моделлю, автомобіль вагою 4000 фунтів матиме прогнозовану паливну економічність 15,6 милі на галон.
Моделі з кількома ознаками
У прикладі, наведеному в цьому розділі, використовується лише одна ознака – вага автомобіля. Проте складніша модель може покладатися на декілька ознак, кожна з яких має окрему вагу ($ w_1 $, $ w_2 $ тощо). Наприклад, модель, яка спирається на п’ять ознак, матиме такий вигляд:
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
Наприклад, модель, яка прогнозує паливну економічність, може додатково використовувати такі ознаки:
- Робочий об’єм двигуна
- Прискорення
- Кількість циліндрів
- Кінські сили
Модель матиме такий вигляд:

Рисунок 5. Модель із п’ятьма ознаками, що прогнозує паливну економічність у милях на галон.
Якщо побудувати графік із точками, які відповідають деяким додатковим ознакам, видно, що вони також мають лінійну залежність від мітки "милі на галон":

Рисунок 6. Робочий об’єм автомобіля в кубічних сантиметрах і його паливна економічність у милях на галон. Зазвичай що більше двигун автомобіля, то менша його паливна економічність у милях на галон.

Рисунок 7. Прискорення автомобіля і його паливна економічність у милях на галон. Зазвичай що довше автомобіль розганяється, то більша його паливна економічність у милях на галон.

Рисунок 8. Кінські сили автомобіля і його паливна економічність у милях на галон. Як правило, що більше кінських сил має автомобіль, то менша його паливна економічність у милях на галон.