What is Minimum Spanning Tree (MST)
Last Updated : 28 Feb, 2025
A spanning tree is defined as a tree-like subgraph of a connected, undirected graph that includes all the vertices of the graph. Or, to say in Layman's words, it is a subset of the edges of the graph that forms a tree (acyclic) where every node of the graph is a part of the tree.
The minimum spanning tree has all the properties of a spanning tree with an added constraint of having the minimum possible weights among all possible spanning trees. Like a spanning tree, there can also be many possible MSTs for a graph.
Properties of a Spanning Tree
The spanning tree holds the below-mentioned principles:
- The number of vertices (V) in the graph and the spanning tree is the same.
- There is a fixed number of edges in the spanning tree which is equal to one less than the total number of vertices ( E = V-1 ).
- The spanning tree should not be disconnected, as in there should only be a single source of component, not more than that.
- The spanning tree should be acyclic, which means there would not be any cycle in the tree.
- The total cost (or weight) of the spanning tree is defined as the sum of the edge weights of all the edges of the spanning tree.
- There can be many possible spanning trees for a graph.
To knowing about the properties of Minimum Spanning Tree, click here.
Minimum Spanning Tree
A minimum spanning tree (MST) is defined as a spanning tree that has the minimum weight among all the possible spanning trees.
The minimum spanning tree has all the properties of a spanning tree with an added constraint of having the minimum possible weights among all possible spanning trees. Like a spanning tree, there can also be many possible MSTs for a graph.
- Let's look at the MST of the above example Graph,
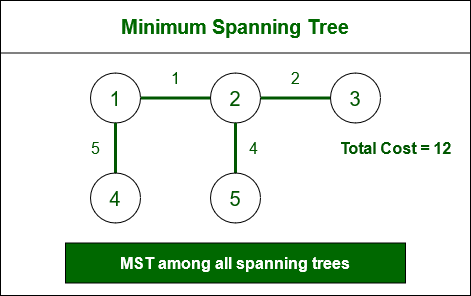Minimum Spanning TreeAlgorithms to find Minimum Spanning Tree
There are several algorithms to find the minimum spanning tree from a given graph, some of them are listed below:
Kruskal's Minimum Spanning Tree Algorithm
This is one of the popular algorithms for finding the minimum spanning tree from a connected, undirected graph. This is a greedy algorithm. The algorithm workflow is as below:
- First, it sorts all the edges of the graph by their weights,
- Then starts the iterations of finding the spanning tree.
- At each iteration, the algorithm adds the next lowest-weight edge one by one, such that the edges picked until now does not form a cycle.
This algorithm can be implemented efficiently using a DSU (Disjoint-Set) data structure to keep track of the connected components of the graph. This is used in a variety of practical applications such as network design, clustering, and data analysis.
Follow the article on "Kruskal's Minimum Spanning Tree Algorithm" for a better understanding and implementation of the algorithm.
Prim's Minimum Spanning Tree Algorithm:
This is also a greedy algorithm. This algorithm has the following workflow:
- It starts by selecting an arbitrary vertex and then adding it to the MST.
- Then, it repeatedly checks for the minimum edge weight that connects one vertex of MST to another vertex that is not yet in the MST.
- This process is continued until all the vertices are included in the MST.
To efficiently select the minimum weight edge for each iteration, this algorithm uses priority_queue to store the vertices sorted by their minimum edge weight currently. It also simultaneously keeps track of the MST using an array or other data structure suitable considering the data type it is storing.
This algorithm can be used in various scenarios such as image segmentation based on color, texture, or other features. For Routing, as in finding the shortest path between two points for a delivery truck to follow.
Follow the article on "Prim's Minimum Spanning Tree Algorithm" for a better understanding and implementation of this algorithm.
Boruvka's Minimum Spanning Tree Algorithm:
This is also a graph traversal algorithm used to find the minimum spanning tree of a connected, undirected graph. This is one of the oldest algorithms. The algorithm works by iteratively building the minimum spanning tree, starting with each vertex in the graph as its own tree. In each iteration, the algorithm finds the cheapest edge that connects a tree to another tree, and adds that edge to the minimum spanning tree. This is almost similar to the Prim's algorithm for finding the minimum spanning tree. The algorithm has the following workflow:
- Initialize a forest of trees, with each vertex in the graph as its own tree.
- For each tree in the forest:
- Find the cheapest edge that connects it to another tree. Add these edges to the minimum spanning tree.
- Update the forest by merging the trees connected by the added edges.
- Repeat the above steps until the forest contains only one tree, which is the minimum spanning tree.
The algorithm can be implemented using a data structure such as a priority queue to efficiently find the cheapest edge between trees. Boruvka's algorithm is a simple and easy-to-implement algorithm for finding minimum spanning trees, but it may not be as efficient as other algorithms for large graphs with many edges.
Follow the article on "Boruvka's Minimum Spanning Tree Algorithm" for a better understanding and implementation of this algorithm.
Applications of Minimum Spanning Trees:
- Network design: Spanning trees can be used in network design to find the minimum number of connections required to connect all nodes. Minimum spanning trees, in particular, can help minimize the cost of the connections by selecting the cheapest edges.
- Image processing: Spanning trees can be used in image processing to identify regions of similar intensity or color, which can be useful for segmentation and classification tasks.
- Biology: Spanning trees and minimum spanning trees can be used in biology to construct phylogenetic trees to represent evolutionary relationships among species or genes.
- Social network analysis: Spanning trees and minimum spanning trees can be used in social network analysis to identify important connections and relationships among individuals or groups.
Follow the article on "Applications of Minimum Spanning Trees" for a better understanding.
Some popular interview problems related to MST:
Similar Reads
Second Best Minimum Spanning Tree Given an undirected graph represented by the array edges[][], where each edges[i] contains three integers [u, v, w], representing an undirected edge from u to v, having distance w. Your task is to find the distance of the second best minimum spanning tree of the given graph.Examples: Input: edges[][
12 min read
Minimum Product Spanning Tree Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. A minimum product spanning tree for a weighted, connected, and undirected graph is a spanning tree with a
15+ min read
Kruskal’s Minimum Spanning Tree (MST) Algorithm A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected, and undirected graph is a spanning tree (no cycles and connects all vertices) that has minimum weight. The weight of a spanning tree is the sum of all edges in the tree. In Kruskal's algorithm, we sort all edges
9 min read
XOR Graph Minimum Spanning Tree Given a complete weighted graph where edges have weights determined by the bitwise-xor operation. The graph has N vertices numbered from 0 to N-1, and each undirected edge between vertices u and v has a weight of u XOR v. The task is to determine the minimum total weight of the spanning tree. Exampl
7 min read
Applications of Minimum Spanning Tree A Minimum Spanning Tree (MST) is a subset of the edges of a connected, undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. It is a way to connect all the vertices in a graph in a way that minimizes the total weight of the edge
3 min read