Trigonometry Table | Trigonometric Ratios and Formulas
Last Updated : 10 May, 2025
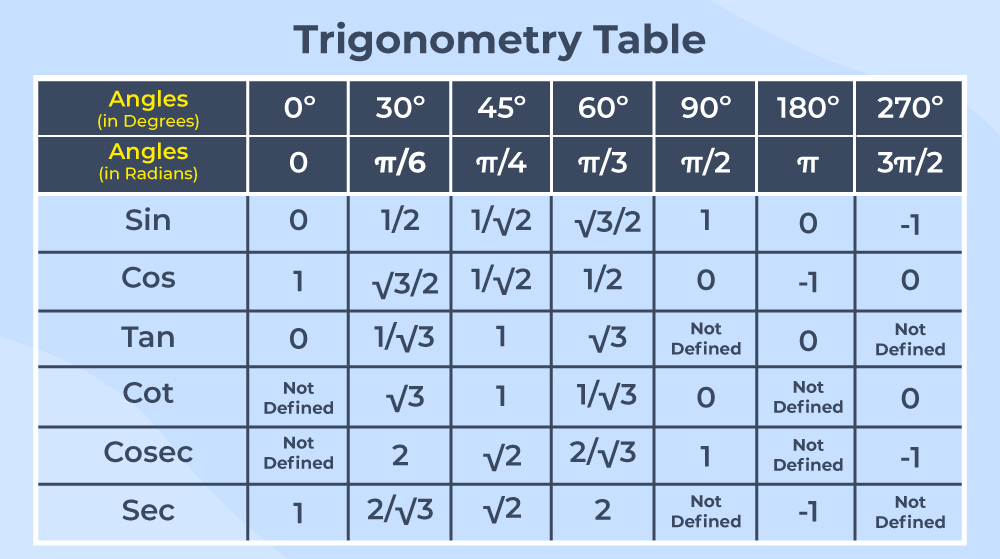
The Trigonometry Table is a standard table that helps us to find the values of trigonometric ratios for standard angles such as 0°, 30°, 45°, 60°, and 90°. It consists of all six trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent.
The most common values of trigonometric ratios are given in the table below:
Read More about the Trick to Remember the Trigonometry Table.
Trigonometric Functions Table
Trigonometry has 6 basic trigonometric functions they are sine, cosine, tangent, cosecant, secant, and cotangent. Now let’s look into the trigonometric functions.
For, any right-angle triangle with perpendicular(P), Base(B), and Hypotenuse(H) the six trigonometric functions are as follows,
Table of Trigonometric Functions |
|---|
| Function | Definition | Representation | Relationship to Sides of a Right Triangle |
|---|
| Sine | Ratio of the perpendicular and the hypotenuse | sin θ | Opposite side / Hypotenuse |
| Cosine | Ratio of base and hypotenuse | cos θ | Adjacent side / Hypotenuse |
| Tangent | The ratio of the sine and cosine of an angle | tan θ | Opposite side / Adjacent side |
| Cosecant | Reciprocal of sin θ | csc θ or cosec θ | Hypotenuse / Opposite side |
| Secant | Reciprocal of cos θ | sec θ | Hypotenuse / Adjacent side |
| Cotangent | Reciprocal of tan θ | cot θ | Adjacent side / Opposite side |
Also, Read about Trigonometric Ratios.
Learn the Trick to Remember Trigonometric Ratios- [SOHCAHTOA]
Silly Owls Hide Cake And Honey Till October Arrives.
How to Create a Trigonometry Table
Study the following steps to create the trigonometric table for standard angles.
Step 1: Create the Table
Create a table and list all the angles, such as 0°, 30°, 45°, 60°, and 90°, in the top row. Enter all trigonometric functions sin, cos, tan, cosec, sec, and cot in the first column.
Step 2: Evaluate the value for all the angles of the sine function.
For finding the values of the sin function, divide 0, 1, 2, 3, and 4 by 4 and take under root of each value, respectively, as,
For the value of sin 0° = √(0/4) = 0. Similarly,
- sin 30° = √(1/4) = 1/2
- sin 45° = √(2/4) = 1/√2
- sin 60° = √(3/4) = √3/2
- sin 90° = √(4/4) = 1
| sin 0° | sin 30° | sin 45° | sin 60° | sin 90° |
|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
Step 3:Evaluate the value for all the angles of the cos function
The value of the cos function is the opposite of the value of the sin function, i.e., cos 0° = sin 90°, cos 30° = sin 60°, and cos 45° = sin 45°, so
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Step 4: Evaluate the value for all the angles of the tan function
The value of the tan function is equal to the sin function divided by the cos function, i.e., tan x = sin x / cos x. The value of all the angles in the tan function is calculated as,
tan 0°= sin 0° / cos 0° = 0/1 = 0, similarly
| tan 0° | tan 30° | tan 45° | tan 60° | tan 90° |
|---|
| 0 | 1/√3 | 1 | √3 | Not Defined |
Step 5: Evaluate the value for all the angles of the cosec function
The value of the cosec function is equal to the reciprocal of the sin function. The value of cosec 0° is obtained by taking the reciprocal of sin 0°
cosec 0° = 1 / sin 0° = 1 / 0 = Not Defined. Similarly,
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|
| Not Defined | 2 | √2 | 2/√3 | 1 |
Step 6: Evaluate the value for all the angles of the sec function
The value of the sec function is equal to the reciprocal of the cos function. The value of sec 0° is obtained by taking the reciprocal of cos 0°
sec 0° = 1 / cos 0° = 1 / 1 = 1. Similarly,
| sec 0° | sec 30° | sec 45° | sec 60° | sec 90° |
|---|
| 1 | 2/√3 | √2 | 2 | Not Defined |
Step 7: Evaluate the value for all the angles of the cot function
The value of the cot function is equal to the reciprocal of the tan function. The value of cot 0° is obtained by taking the reciprocal of tan 0°
cot 0° = 1 /tan 0° = 1 / 0 = Not defined. Similarly,
| cot 0° | cot 30° | cot 45° | cot 60° | cot 90° |
|---|
| Not Defined | √3 | 1 | 1/√3 | 0 |
In this way, we can create the following trigonometric ratios table:
Degrees and Radians Trigonometric Table |
|---|
| Angle (in degrees) | Angle (in radians) | Sin | Cos | Tan | Cosec | Sec | Cot |
|---|
| 0° | 0 | 0 | 1 | 0 | Undefined | 1 | Undefined |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 | 2 | 2/√3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | 2/√3 | 2 | 1/√3 |
| 90° | π/2 | 1 | 0 | Undefined | 1 | Undefined | 0 |
Next Article: Trigonometry Formulas.
Similar Reads
Trigonometry Formulas - List of All Trigonometric Identities and Formulas Trigonometry formulas are equations that relate the various trigonometric ratios to each other. They are essential for solving a wide range of problems in mathematics, physics, engineering, and other fields.Some of the most important trigonometric formulas are:Basic Definitions: These formulas defin
9 min read
Trick to Remember Trigonometric Table Trigonometric table is a chart that provides the values of trigonometric functions—sine, cosine, and tangent—for specific angles.Sine (sin): The sine of an angle is the ratio of the length of the opposite side to the hypotenuse in a right-angled triangle.Cosine (cos): The cosine of an angle is the r
2 min read
Trigonometric Ratios of Some Specific Angles Trigonometry is all about triangles or to be more precise the relationship between the angles and sides of a triangle (right-angled triangle). In this article, we will be discussing the ratio of sides of a right-angled triangle concerning its acute angle called trigonometric ratios of the angle and
6 min read
Trigonometry Practice Questions Hard Trigonometry can be challenging, especially when you're tackling advanced problems. In this article, we’ll focus on a series of hard trigonometry practice questions designed to test your understanding of key concepts.Whether you’re preparing for exams or looking to strengthen your problem-solving sk
6 min read
Trigonometry Practice Questions Easy Trigonometry can be tricky, especially for class 10 and 11 students when trigonometric ratios and identities are involved. In this article, we have collected a list of questions on all the important trigonometry concepts and formulas.Solving these questions, ranging from easy to hard will help you b
3 min read