The Trie data structure is a tree-like structure used for storing a dynamic set of strings. It allows for efficient retrieval and storage of keys, making it highly effective in handling large datasets. Trie supports operations such as insertion, search, deletion of keys, and prefix searches. In this article, we will explore the insertion and search operations and prefix searches in Trie Data Structure.
 Trie Data Structure
Trie Data Structure
Representation of Trie Node
- Trie data structure consists of nodes connected by edges.
- Each node represents a character or a part of a string.
- The root node acts as a starting point and does not store any character.
C++ class TrieNode { public: // pointer array for child nodes of each node TrieNode* children[26]; // Used for indicating ending of string bool isLeaf; TrieNode() { // initialize the wordEnd variable with false // initialize every index of childNode array with NULL isLeaf = false; for (int i = 0; i < 26; i++) { children[i] = nullptr; } } }; public class TrieNode { // Array for child nodes of each node TrieNode[] children; // Used for indicating the end of a string boolean isEndOfWord; // Constructor public TrieNode() { // Initialize the wordEnd // variable with false isEndOfWord = false; // Initialize every index of // the child array with null // In Java, we do not have to // explicitely assign null as // the values are by default // assigned as null children = new TrieNode[26]; } } class TrieNode: def __init__(self): self.children = [None] * 26 self.isEndOfWord = False
class TrieNode { public TrieNode[] children = new TrieNode[26]; public bool isLeaf = false; } class TrieNode { constructor() { // Initialize the child Node // array with 26 nulls this.children = Array(26).fill(null); // Initialize wordEnd to the false // indicating that no word ends here yet this.isEndOfWord = false; } } Insertion in Trie Data Structure - O(n) Time and O(n) Space
 Insert Operation in Trie Data Structure
Insert Operation in Trie Data StructureInserting "and" in Trie data structure:
- Start at the root node: The root node has no character associated with it and its wordEnd value is 0, indicating no complete word ends at this point.
- First character "a": Calculate the index using 'a' - 'a' = 0. Check if the child[0] is null. Since it is, create a new TrieNode with the character "a", wordEnd set to 0, and an empty array of pointers. Move to this new node.
- Second character "n": Calculate the index using 'n' - 'a' = 13. Check if child[13] is null. It is, so create a new TrieNode with the character "n", wordEnd set to 0, and an empty array of pointers. Move to this new node.
- Third character "d": Calculate the index using 'd' - 'a' = 3. Check if child[3] is null. It is, so create a new TrieNode with the character "d", wordEnd set to 1 (indicating the word "and" ends here).
Inserting "ant" in Trie data structure:
- Start at the root node: Root node doesn't contain any data but it keep track of every first character of every string that has been inserted.
- First character "a": Calculate the index using 'a' - 'a' = 0. Check if the child[0] is null. We already have the "a" node created from the previous insertion. so move to the existing "a" node.
- First character "n": Calculate the index using 'n' - 'a' = 13. Check if child[13] is null. It's not, so move to the existing "n" node.
- Second character "t": Calculate the index using 't' - 'a' = 19. Check if child[19] is null. It is, so create a new TrieNode with the character "t", wordEnd set to 1 (indicating the word "ant" ends here).
C++ // Method to insert a key into the Trie void insert(TrieNode* root, const string& key) { // Initialize the curr pointer with the root node TrieNode* curr = root; // Iterate across the length of the string for (char c : key) { // Check if the node exists for the // current character in the Trie if (curr->children[c - 'a'] == nullptr) { // If node for current character does // not exist then make a new node TrieNode* newNode = new TrieNode(); // Keep the reference for the newly // created node curr->children[c - 'a'] = newNode; } // Move the curr pointer to the // newly created node curr = curr->children[c - 'a']; } // Mark the end of the word curr->isLeaf = true; } // Function to insert a key into the Trie void insert(struct TrieNode* root, const char* key) { struct TrieNode* curr = root; while (*key) { int index = *key - 'a'; if (!curr->children[index]) { curr->children[index] = getNode(); } curr = curr->children[index]; key++; } curr->isEndOfWord = true; } // Method to insert a key into the Trie static void insert(TrieNode root, String key) { // Initialize the curr pointer with the root node TrieNode curr = root; // Iterate across the length of the string for (char c : key.toCharArray()) { // Check if the node exists for the // current character in the Trie if (curr.children[c - 'a'] == null) { // If node for current character does // not exist then make a new node TrieNode newNode = new TrieNode(); // Keep the reference for the newly // created node curr.children[c - 'a'] = newNode; } // Move the curr pointer to the // newly created node curr = curr.children[c - 'a']; } // Mark the end of the word curr.isEndOfWord = true; } # Method to insert a key into the Trie def insert(root, key): # Initialize the curr pointer with the root node curr = root # Iterate across the length of the string for c in key: # Check if the node exists for the # current character in the Trie index = ord(c) - ord('a') if curr.children[index] is None: # If node for current character does # not exist then make a new node new_node = TrieNode() # Keep the reference for the newly # created node curr.children[index] = new_node # Move the curr pointer to the # newly created node curr = curr.children[index] # Mark the end of the word curr.isEndOfWord = True // Method to insert a key into the Trie public static void Insert(TrieNode root, string key) { // Initialize the curr pointer with the root node TrieNode curr = root; // Iterate across the length of the string foreach(char c in key) { // Check if the node exists for the current // character in the Trie if (curr.children[c - 'a'] == null) { // If node for current character does // not exist then make a new node TrieNode newNode = new TrieNode(); // Keep the reference for the newly created node curr.children[c - 'a'] = newNode; } // Move the curr pointer to the newly created node curr = curr.children[c - 'a']; } // Mark the end of the word curr.isLeaf = true; } // Method to insert a key into the Trie function insert(root, key) { // Initialize the curr pointer with the root node let curr = root; // Iterate across the length of the string for (let c of key) { // Check if the node exists for the // current character in the Trie let index = c.charCodeAt(0) - 'a'.charCodeAt(0); if (curr.children[index] === null) { // If node for current character does // not exist then make a new node let newNode = new TrieNode(); // Keep the reference for the newly // created node curr.children[index] = newNode; } // Move the curr pointer to the // newly created node curr = curr.children[index]; } // Mark the end of the word curr.isEndOfWord = true; } Time Complexity: O(n), where n is the length of the word to insert.
Auxiliary Space: O(n)
Searching in Trie Data Structure - O(n) Time and O(1) Space
Searching for a key in Trie data structure is similar to its insert operation. However, It only compares the characters and moves down. The search can terminate due to the end of a string or lack of key in the trie.
Here's a visual representation of searching word "dad" in Trie data structure:
Let's assume that we have successfully inserted the words "and", "ant", and "dad" into our Trie, and we have to search for specific words within the Trie data structure. Let's try searching for the word "dad":
 Search Operation in Trie Data Structure
Search Operation in Trie Data Structure
Here's a visual representation of searching word "dad" in Trie data structure:
Let's assume that we have successfully inserted the words "and", "ant", and "dad" into our Trie, and we have to search for specific words within the Trie data structure. Let's try searching for the word "dad":
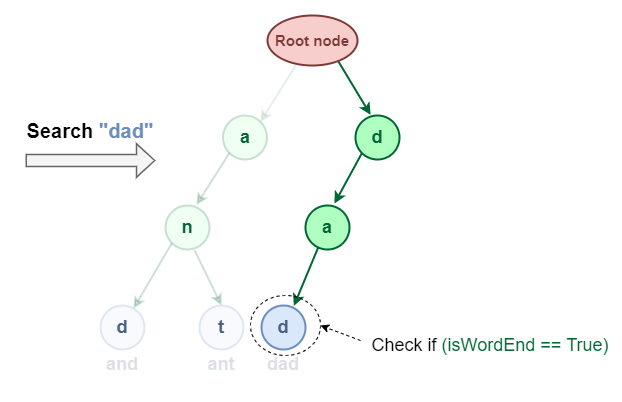
- We start at the root node.
- We follow the branch corresponding to the character 'd'.
- We follow the branch corresponding to the character 'a'.
- We follow the branch corresponding to the character 'd'.
- We reach the end of the word and wordEnd flag is 1.
- This means that "dad" is present in the Trie.
C++ // Method to search a key in the Trie bool search(TrieNode* root, const string& key) { // Initialize the curr pointer with the root node TrieNode* curr = root; // Iterate across the length of the string for (char c : key) { // Check if the node exists for the // current character in the Trie if (curr->children[c - 'a'] == nullptr) return false; // Move the curr pointer to the // already existing node for the // current character curr = curr->children[c - 'a']; } // Return true if the word exists // and is marked as ending return curr->isLeaf; } // Function to search a key in the Trie bool search(struct TrieNode* root, const char* key) { struct TrieNode* curr = root; while (*key) { int index = *key - 'a'; if (!curr->children[index]) { return false; } curr = curr->children[index]; key++; } return (curr != NULL && curr->isEndOfWord); } // Method to search a key in the Trie static boolean search(TrieNode root, String key) { // Initialize the curr pointer with the root node TrieNode curr = root; // Iterate across the length of the string for (char c : key.toCharArray()) { // Check if the node exists for the // current character in the Trie if (curr.children[c - 'a'] == null) return false; // Move the curr pointer to the // already existing node for the // current character curr = curr.children[c - 'a']; } // Return true if the word exists // and is marked as ending return curr.isEndOfWord; } # Method to search a key in the Trie def search(root, key): # Initialize the curr pointer with the root node curr = root # Iterate across the length of the string for c in key: # Check if the node exists for the # current character in the Trie index = ord(c) - ord('a') if curr.children[index] is None: return False # Move the curr pointer to the # already existing node for the # current character curr = curr.children[index] # Return true if the word exists # and is marked as ending return curr.isEndOfWord // Method to search a key in the Trie public static bool Search(TrieNode root, string key) { // Initialize the curr pointer with the root node TrieNode curr = root; // Iterate across the length of the string foreach(char c in key) { // Check if the node exists for the current // character in the Trie if (curr.children[c - 'a'] == null) return false; // Move the curr pointer to the already // existing node for the current character curr = curr.children[c - 'a']; } // Return true if the word exists and // is marked as ending return curr.isLeaf; } // Method to search a key in the Trie function search(root, key) { // Initialize the curr pointer with the root node let curr = root; // Iterate across the length of the string for (let c of key) { // Check if the node exists for the // current character in the Trie let index = c.charCodeAt(0) - 'a'.charCodeAt(0); if (curr.children[index] === null) return false; // Move the curr pointer to the // already existing node for the // current character curr = curr.children[index]; } // Return true if the word exists // and is marked as ending return curr.isEndOfWord; } Time Complexity: O(n), where n is the length of the word to search.
Auxiliary Space: O(1)
Prefix Searching in Trie Data Structure - O(n) Time and O(1) Space
Searching for a prefix in a Trie data structure is similar to searching for a key, but the search does not need to reach the end of the word. Instead, we stop as soon as we reach the end of the prefix or if any character in the prefix doesn't exist in the Trie.
Here's a visual representation of prefix searching for the word 'da' in the Trie data structure:
Let's assume that we have successfully inserted the words 'and', 'ant', and 'dad' into our Trie. Now, let's search for the prefix 'da' within the Trie data structure.

- We start at the root node.
- We follow the branch corresponding to the character 'd'.
- We move to the node corresponding to the character 'a'.
- We reach the end of the prefix "da". Since we haven't encountered any missing characters along the way, we return
true.
C++ // Method to Seach Prefix key in Trie bool isPrefix(TrieNode *root, string &key) { TrieNode *current = root; for (char c : key) { int index = c - 'a'; // If character doesn't exist, return false if (current->children[index] == nullptr) { return false; } current = current->children[index]; } return true; } boolean isPrefix(TrieNode root, String key) { TrieNode current = root; for (char c : key.toCharArray()) { int index = c - 'a'; // If character doesn't exist, return false if (current.children[index] == null) { return false; } current = current.children[index]; } return true; } def is_prefix(root, key): current = root for c in key: index = ord(c) - ord('a') # If character doesn't exist, return false if current.children[index] is None: return False current = current.children[index] return True bool IsPrefix(TrieNode root, string key) { TrieNode current = root; foreach(char c in key) { int index = c - 'a'; // If character doesn't exist, return false if (current.Children[index] == null) { return false; } current = current.Children[index]; } return true; } function isPrefix(root, key) { let current = root; for (let c of key) { let index = c.charCodeAt(0) - "a".charCodeAt(0); // If character doesn't exist, return false if (current.children[index] === null) { return false; } current = current.children[index]; } return true; } Time Complexity: O(n), where n is the length of the word to search.
Auxiliary Space: O(1)
Implementation of Insert, Search and Prefix Searching Operations in Trie Data Structure
Now that we've learned how to insert words into a Trie, search for complete words, and perform prefix searches, let's do some hands-on practice.
We'll start by inserting the following words into the Trie: ["and", "ant", "do", "dad"].
Then, we'll search for the presence of these words: ["do", "gee", "bat"].
Finally, we'll check for the following prefixes: ["ge", "ba", "do", "de"].
Steps-by-step approach:
- Create a root node with the help of TrieNode() constructor.
- Store a collection of strings that have to be inserted in the Trie in a vector of strings say, arr.
- Inserting all strings in Trie with the help of the insertKey() function,
- Search strings with the help of searchKey() function.
- Prefix searching with the help of isPrefix() function.
C++ #include <bits/stdc++.h> using namespace std; class TrieNode { public: // Array for children nodes of each node TrieNode *children[26]; // for end of word bool isLeaf; TrieNode() { isLeaf = false; for (int i = 0; i < 26; i++) { children[i] = nullptr; } } }; // Method to insert a key into the Trie void insert(TrieNode *root, const string &key) { // Initialize the curr pointer with the root node TrieNode *curr = root; // Iterate across the length of the string for (char c : key) { // Check if the node exists for the // current character in the Trie if (curr->children[c - 'a'] == nullptr) { // If node for current character does // not exist then make a new node TrieNode *newNode = new TrieNode(); // Keep the reference for the newly // created node curr->children[c - 'a'] = newNode; } // Move the curr pointer to the // newly created node curr = curr->children[c - 'a']; } // Mark the end of the word curr->isLeaf = true; } // Method to search a key in the Trie bool search(TrieNode *root, const string &key) { if (root == nullptr) { return false; } // Initialize the curr pointer with the root node TrieNode *curr = root; // Iterate across the length of the string for (char c : key) { // Check if the node exists for the // current character in the Trie if (curr->children[c - 'a'] == nullptr) return false; // Move the curr pointer to the // already existing node for the // current character curr = curr->children[c - 'a']; } // Return true if the word exists // and is marked as ending return curr->isLeaf; } // Method to check if a prefix exists in the Trie bool isPrefix(TrieNode *root, const string &prefix) { // Initialize the curr pointer with the root node TrieNode *curr = root; // Iterate across the length of the prefix string for (char c : prefix) { // Check if the node exists for the current character in the Trie if (curr->children[c - 'a'] == nullptr) return false; // Move the curr pointer to the already existing node // for the current character curr = curr->children[c - 'a']; } // If we reach here, the prefix exists in the Trie return true; } int main() { // Create am example Trie TrieNode *root = new TrieNode(); vector<string> arr = {"and", "ant", "do", "dad"}; for (const string &s : arr) { insert(root, s); } // One by one search strings vector<string> searchKeys = {"do", "gee", "bat"}; for (string &s : searchKeys){ if(search(root, s)) cout << "true "; else cout << "false "; } cout<<"\n"; // One by one search for prefixes vector<string> prefixKeys = {"ge", "ba", "do", "de"}; for (string &s : prefixKeys){ if (isPrefix(root, s)) cout << "true "; else cout << "false "; } return 0; } class TrieNode { TrieNode[] children; boolean isLeaf; TrieNode() { children = new TrieNode[26]; isLeaf = false; } } public class Trie { TrieNode root; public Trie() { root = new TrieNode(); } // Method to insert a key into the Trie public void insert(String key) { TrieNode curr = root; for (char c : key.toCharArray()) { if (curr.children[c - 'a'] == null) { curr.children[c - 'a'] = new TrieNode(); } curr = curr.children[c - 'a']; } curr.isLeaf = true; } // Method to search a key in the Trie public boolean search(String key) { TrieNode curr = root; for (char c : key.toCharArray()) { if (curr.children[c - 'a'] == null) { return false; } curr = curr.children[c - 'a']; } return curr.isLeaf; } // Method to check if a prefix exists in the Trie public boolean isPrefix(String prefix) { TrieNode curr = root; for (char c : prefix.toCharArray()) { if (curr.children[c - 'a'] == null) { return false; } curr = curr.children[c - 'a']; } return true; } public static void main(String[] args) { Trie trie = new Trie(); String[] arr = {"and", "ant", "do", "dad"}; for (String s : arr) { trie.insert(s); } String[] searchKeys = { "do", "gee", "bat" }; for (String s : searchKeys) { if (trie.search(s)) System.out.print("true "); else System.out.print("false "); } System.out.println(); String[] prefixKeys = { "ge", "ba", "do", "de" }; for (String s : prefixKeys) { if (trie.isPrefix(s)) System.out.print("true "); else System.out.print("false "); } } } class TrieNode: def __init__(self): self.children = [None] * 26 self.isLeaf = False class Trie: def __init__(self): self.root = TrieNode() # Method to insert a key into the Trie def insert(self, key): curr = self.root for c in key: index = ord(c) - ord('a') if curr.children[index] is None: curr.children[index] = TrieNode() curr = curr.children[index] curr.isLeaf = True # Method to search a key in the Trie def search(self, key): curr = self.root for c in key: index = ord(c) - ord('a') if curr.children[index] is None: return False curr = curr.children[index] return curr.isLeaf # Method to check if a prefix exists in the Trie def isPrefix(self, prefix): curr = self.root for c in prefix: index = ord(c) - ord('a') if curr.children[index] is None: return False curr = curr.children[index] return True if __name__ == '__main__': trie = Trie() arr = ["and", "ant", "do", "dad"] for s in arr: trie.insert(s) searchKeys = ["do", "gee", "bat"] for s in searchKeys: if trie.search(s): print("true", end= " ") else: print("false", end=" ") print() prefixKeys = ["ge", "ba", "do", "de"] for s in prefixKeys: if trie.isPrefix(s): print("true", end = " ") else: print("false", end = " ") // Using System.Collections.Generic; using System; class TrieNode { public TrieNode[] children = new TrieNode[26]; public bool isLeaf; public TrieNode() { isLeaf = false; for (int i = 0; i < 26; i++) { children[i] = null; } } } class Trie { private TrieNode root; public Trie() { root = new TrieNode(); } // Method to insert a key into the Trie public void Insert(string key) { TrieNode curr = root; foreach(char c in key) { if (curr.children[c - 'a'] == null) { curr.children[c - 'a'] = new TrieNode(); } curr = curr.children[c - 'a']; } curr.isLeaf = true; } // Method to search a key in the Trie public bool Search(string key) { TrieNode curr = root; foreach(char c in key) { if (curr.children[c - 'a'] == null) return false; curr = curr.children[c - 'a']; } return curr.isLeaf; } // Method to check if a prefix exists in the Trie public bool isPrefix(string prefix) { TrieNode curr = root; foreach(char c in prefix) { if (curr.children[c - 'a'] == null) return false; curr = curr.children[c - 'a']; } return true; } } class GfG{ static void Main() { Trie trie = new Trie(); string[] arr = { "and", "ant", "do", "dad"}; foreach(string s in arr) { trie.Insert(s); } // One by one search strings string[] searchKeys = { "do", "gee", "bat" }; foreach(string s in searchKeys){ if (trie.Search(s)) Console.Write("true "); else Console.Write("false "); } Console.WriteLine(); // One by one search for prefixes string[] prefixKeys = { "ge", "ba", "do", "de" }; foreach(string s in prefixKeys){ if (trie.isPrefix(s)) Console.Write("true "); else Console.Write("false "); } } } // TrieNode class class TrieNode { constructor() { this.children = new Array(26).fill(null); this.isLeaf = false; } } // Trie class class Trie { constructor() { this.root = new TrieNode(); } // Method to insert a key into the Trie insert(key) { let curr = this.root; for (let c of key) { if (curr.children[c.charCodeAt(0) - "a".charCodeAt(0)] === null) { curr.children[c.charCodeAt(0) - "a".charCodeAt(0)] = new TrieNode(); } curr = curr.children[c.charCodeAt(0) - "a".charCodeAt(0)]; } curr.isLeaf = true; } // Method to search a key in the Trie search(key) { let curr = this.root; for (let c of key) { if (curr.children[c.charCodeAt(0) - "a".charCodeAt(0)] === null) return false; curr = curr.children[c.charCodeAt(0) - "a".charCodeAt(0)]; } return curr.isLeaf; } // Method to check if a prefix exists in the Trie isPrefix(prefix) { let curr = this.root; for (let c of prefix) { if (curr.children[c.charCodeAt(0) - "a".charCodeAt(0)] === null) return false; curr = curr.children[c.charCodeAt(0) - "a".charCodeAt(0)]; } return true; } } const trie = new Trie(); const arr = [ "and", "ant", "do", "dad"]; for (let s of arr) { trie.insert(s); } // One by one search strings const searchKeys = [ "do", "gee", "bat" ]; console.log(searchKeys.map(s => trie.search(s) ? "true" : "false").join(" ")); // One by one search for prefixes const prefixKeys = [ "ge", "ba", "do", "de" ]; console.log(prefixKeys.map(s => trie.isPrefix(s) ? "true" : "false").join(" ")); Outputtrue false false false false true false
Complexity Analysis of Trie Data Structure
| Operation | Time Complexity |
|---|
| Insertion | O(n) Here n is the length of the string inserted |
|---|
| Searching | O(n) Here n is the length of the string searched |
|---|
Prefix Searching | O(n) Here n is the length of the string searched |
|---|
Related Articles:
Practice Problems:
Similar Reads
Tree Data Structure Tree Data Structure is a non-linear data structure in which a collection of elements known as nodes are connected to each other via edges such that there exists exactly one path between any two nodes.Basics of Tree Data StructureIntroduction to TreeTypes of Trees in Data StructuresApplications of tr
4 min read
Data Structures Tutorial Data structures are the fundamental building blocks of computer programming. They define how data is organized, stored, and manipulated within a program. Understanding data structures is very important for developing efficient and effective algorithms. What is Data Structure?A data structure is a st
2 min read
Trie Data Structure Tutorial The trie data structure, also known as a prefix tree, is a tree-like data structure used for efficient retrieval of key-value pairs. It is commonly used for implementing dictionaries and autocomplete features, making it a fundamental component in many search algorithms. In this article, we will expl
15+ min read
Binary Tree Data Structure A Binary Tree Data Structure is a hierarchical data structure in which each node has at most two children, referred to as the left child and the right child. It is commonly used in computer science for efficient storage and retrieval of data, with various operations such as insertion, deletion, and
3 min read
What is Data Structure? A data structure is a way of organizing and storing data in a computer so that it can be accessed and used efficiently. It refers to the logical or mathematical representation of data, as well as the implementation in a computer program.Classification:Data structures can be classified into two broad
2 min read