Secant Formula - Concept, Formulae, Solved Examples
Last Updated : 22 Jul, 2024
Secant is one of the six basic trigonometric ratios and its formula is secant(θ) = hypotenuse/base, it is also represented as, sec(θ). It is the inverse(reciprocal) ratio of the cosine function and is the ratio of the Hypotenus and Base sides in a right-angle triangle.
In this article, we have covered, about Scant Formula, related examples and others in detail.
What are Trigonometric Ratios?
Trigonometric ratios are ratios of sides in a triangle and there are six trigonometric ratios. In a right-angle triangle, the six trigonometric ratios are defined as:

The six trigonometric ratios or functions are,
- sin θ = (Opposite Side/Hypotenuse = AB/AC
- cos θ = Adjacent Side/Hypotenuse = BC/AC
- tan θ = Opposite side/adjacent side = AB/BC
- cosec θ = 1/sin θ = Hypotenuse/Opposite Side = AC/AB
- sec θ = 1/cos θ = Hypotenuse/Adjacent Side = AC/BC
- cot θ = 1/tan θ = Adjacent Side/Opposite Side = BC/AB
Secant of an angle in a right-angled triangle is the ratio of the length of the hypotenuse to the length of the adjacent side to the given angle. We write a secant function as "sec". Let PQR be a right-angled triangle, and "θ" be one of its acute angles.
 Secant Formula
Secant FormulaAn adjacent side is a side that is adjacent to the angle "θ", and a hypotenuse is a side opposite to the right angle and also the longest side of a right-angled triangle. A secant function is a reciprocal function of the cosine function.
Now, the secant formula for the given angle "θ" is,
sec θ = Hypotenuse/Adjacent side
or
sec θ = Hypotenuse/Base
Some basic trigonometric formulae in terms of other trigonometric formulae are discussed below
Secant Function in Quadrants
- Secant function is positive in the first and fourth quadrants and negative in the second and third quadrants.
Degrees | Quadrant | Sign of Secant function |
|---|
0° to 90° | 1st quadrant | + (positive) |
90° to 180° | 2nd quadrant | – (negative) |
180° to 270° | 3rd quadrant | – (negative) |
270° to 360° | 4th quadrant | + (positive) |
Negative Angle Identity of a Secant Function
- Secant of a negative angle is always equal to the secant of the angle.
sec (-θ) = sec θ
Secant Function in terms of Cosine Function
- A secant function is a reciprocal function of the cosine function.
sec θ = 1/cos θ
Secant Function in terms of Sine Function
Secant function in terms of the sine function can be written as,
sec θ = ±1/√(1-sin2θ)
We know that
sec θ = 1/cos θ
From Pythagorean identities we have;
cos2 θ + sin2 θ = 1
⇒ cos θ = √1 - sin2 θ
Hence, sec θ = ± 1/√(sin2 θ - 1)
Secant Function in terms of Tangent function
The secant function in terms of the tangent function can be written as,
sec θ = ±√(1 + tan2θ)
From Pythagorean identities, we have,
sec2 θ – tan2 θ = 1
⇒ sec2θ = 1 + tan2θ
Hence, sec θ = ±√(1 + tan2θ)
Secant Function in terms of Cosecant Function
The secant function in terms of the cosecant function can be written as,
If θ is positive in the first quadrant, then
sec θ = cosec (90 - θ) or cosec (π/2 - θ)
(or)
sec θ = cosec θ/√(cosec2 θ - 1)
We have,
sec θ = 1/√(1-sin2θ)
We know that sin θ = 1/cosec θ
By substituting sin θ = 1/cosec θ in the above equation, we get
sec θ = 1/√(1 - (1/cosec2θ)
Hence, sec θ = (cosec θ)/√(cosec2 θ - 1)
Secant Function in terms of Cotangent Function
The secant function in terms of the cotangent function can be written as,
sec θ = ±√(cot2θ + 1)/cotθ
From Pythagorean identities, we have,
sec2 θ – tan2 θ = 1
⇒ sec2θ = 1 + tan2θ
We know that tan θ = 1/cot θ
By substituting tan θ = 1/cot θ in the above equation, we get
⇒ sec2 θ = 1 + (1/cot2θ)
⇒ sec2 θ = (cot2 θ + 1)/cot2θ
Hence, sec θ = ±√(cot2θ + 1)/cotθ
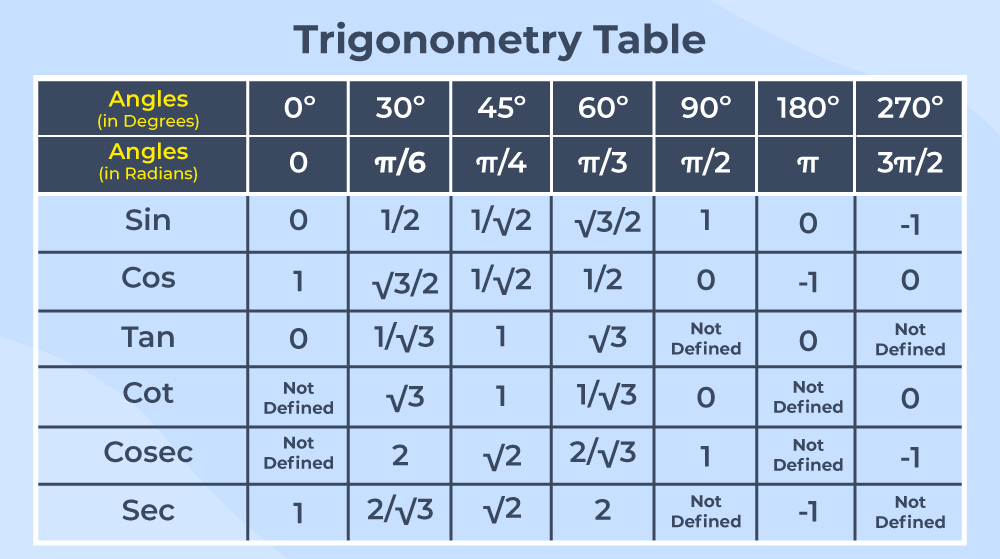
Trigonometric Ratio Table
The trigonometric table is added below:
Problem 1: Find the value of sec θ, if sin θ = 1/3.
Solution:
Given,
sin θ = 1/3
We know that,
sec θ = 1/√(1-sin2θ)
⇒ sec θ = 1/(1 - (1/3)2)
= 1/√(1 - (1/9))
= 1/√(8/9) = 3/2√2
Hence, sec θ = 3/2√2
Problem 2: Find the value of sec x if tan x = 5/12 and x is the first quadrant angle.
Solution:
Given,
tan x = 5/12
From the Pythagorean identities, we have,
sec2 x – tan2 x = 1
⇒ sec2x = 1 + tan2x
⇒ sec2x = 1 + (5/12)2
⇒ sec2x = 1 +(25/144) =169/144
⇒ sec x = √(169/144) = ±13/12
Since x is the first quadrant angle, sec x is positive.
Hence, sec x = 13/12
Problem 3: If cosec α = 25/24, then find the value of sec α.
Solution:
Given,
cosec α = 25/24
We know that,
cosec α = 25/24 = hypotenuse/opposite side
adjacent side = √[(hypotenuse)2 - (opposite side)2]
= √[(25)2 - (24)2] = √(625 - 576)
= √49 = 7
Now, sec α = hypotenuse/adjacent side = 25/7
Hence, sec α = 25/7
Problem 4: Find the value of sec θ, if cos θ = 2/3.
Solution:
Given,
cos θ = 2/3
We know that,
A secant function is the reciprocal function of a cosine function.
So, sec θ = 1/cos θ
= 1/(2/3) = 3/2
Hence, sec θ = 3/2
Problem 5: A right triangle has the following measurements: hypotenuse = 10 units, base = 8 units, and perpendicular = 6 units. Now, find sec θ using the secant formula.
Solution:
Given,
Hypotenuse = 10 units
Base = 8 units
Perpendicular = 6 units
We know that,
sec θ = hypotenuse/base
= 10/8 = 5/4
Hence, sec θ = 5/4.
Problem 6: Determine the side of a right-angled triangle whose hypotenuse is 15 units and whose base angle with the side is 45 degrees.
Solution:
Given,
θ = 45 degree
Hypotenuse = 15 units
Using the secant formula,
sec θ = hypotenuse/base
sec 45 =15/B
√2 = 15/B
B = 15/√2 = 15√2/2
B = 7.5√2
Hence, the base of the triangle is 7.5√2 units.
Similar Reads
Bond Pricing : Meaning, Formula, Examples & Use What is Bond Pricing?Bond pricing is a fundamental concept in finance that plays a pivotal role in the functioning of financial markets. At its core, a bond represents a contractual agreement between an issuer (such as a corporation or government entity) and an investor, wherein the issuer borrows f
5 min read
Area of a Triangle | Formula and Examples The area of the triangle is a basic geometric concept that calculates the measure of the space enclosed by the three sides of the triangle. The formulas to find the area of a triangle include the base-height formula, Heron's formula, and trigonometric methods.The area of triangle is generally calcul
6 min read
CBSE Class 10th Maths Formulas: Chapter Wise Formula and Points Mathematics is one of the most scoring subject in CBSE Class 10th board exam. So Students are advised to prepare well for Math in order to score good marks in CBSE Class 10 board exam. GeeksforGeeks has curated the chapter wise Math formulae for CBSE Class 10th exam. These Formulae include chapters
15+ min read
Sin Cos Formulas in Trigonometry with Examples Sin Cos Formulas in Trigonometry: Trigonometry, as its name implies, is the study of triangles. It is an important branch of mathematics that studies the relationship between side lengths and angles of the right triangle and also aids in determining the missing side lengths or angles of a triangle.
8 min read
Exponential Function Formulas The exponential function, typically denoted as ex or expâ¡(x), is a mathematical function where 'e' is the base of the natural logarithm, approximately equal to 2.71828. The formula for the exponential function is:f(x) = ax This function is characterized by the fact that the rate of growth is proport
5 min read