Linear Algebra

Which one of the following does NOT equal to 

Let A be the 2 × 2 matrix with elements a₁₁ = a₁₂ = a₂₁ = +1 and a₂₂ = −1. Then the eigenvalues of the matrix A¹⁹ are

Consider the matrix as given below.

[Tex]\begin{bmatrix} 1&2&3\\ 0&4&7\\ 0&0&3\end{bmatrix}[/Tex]

Which one of the following options provides the CORRECT values of the eigenvalues of the matrix?

Consider the following matrix 

[Tex]A = \begin{bmatrix} 2 & 3 \\ x & y \end{bmatrix}[/Tex]

If the eigenvalues of A are 4 and 8, then

 

Note -This was Numerical Type question.

How many of the following matrices have an eigenvalue 1?

[Tex]\left[\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right],\left[\begin{array}{ll}0 & 1 \\ 0 & 0 \end{array}\right],\left[\begin{array}{cc}1 & -1 \\1 & 1 \end{array}\right][/Tex] and [Tex]\left[\begin{array}{cc} -1 & 0 \\1 & -1 \end{array}\right][/Tex]

If the matrix A is such that [Tex]A = \begin{bmatrix}2 \\-4 \\7\end{bmatrix}\begin{bmatrix}1 & 9 & 5\end{bmatrix}[/Tex], then the determinant of A is equal to

The product of the non-zero eigenvalues of the matrix

1 0 0 0 1
0 1 1 1 0
0 1 1 1 0
0 1 1 1 0
1 0 0 0 1

is ______

Which one of the following statements is TRUE about every 
 

Consider the set H of all 3 × 3 matrices of the type 
 

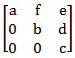
where a, b, c, d, e and f are real numbers and abc ≠ 0. Under the matrix multiplication operation, the set H is