Topological Sorting in Python

Last Updated : 04 Mar, 2025

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge uv, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.

Example:

Input: Graph :
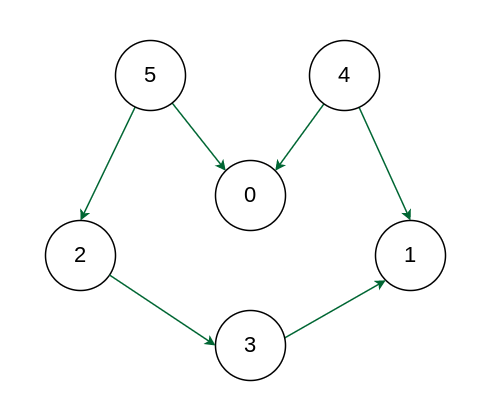Example
Output: 5 4 2 3 1 0
Explanation: The first vertex in topological sorting is always a vertex with an in-degree of 0 (a vertex with no incoming edges). A topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. Another topological sorting of the following graph is “4 5 2 3 1 0”.

Topological sorting can be implemented recursively and non-recursively. First, we show the clearer recursive version, then provide the non-recursive version with analysis.

Recursive DFS-Based Topological Sorting

This approach uses Depth-First Search (DFS) and recursion to find the topological order of a Directed Acyclic Graph (DAG). It explores all dependencies first and then adds the node to a stack, ensuring the correct order. The final sequence is obtained by reversing the stack.

Python

from collections import defaultdict  #Class to represent a graph class Graph:     def __init__(self,vertices):         self.graph = defaultdict(list) #dictionary containing adjacency List         self.V = vertices #No. of vertices      # function to add an edge to graph     def addEdge(self,u,v):         self.graph[u].append(v)      # A recursive function used by topologicalSort     def topologicalSortUtil(self,v,visited,stack):          # Mark the current node as visited.         visited[v] = True          # Recur for all the vertices adjacent to this vertex         for i in self.graph[v]:             if visited[i] == False:                 self.topologicalSortUtil(i,visited,stack)          # Push current vertex to stack which stores result         stack.insert(0,v)      # The function to do Topological Sort. It uses recursive     # topologicalSortUtil()     def topologicalSort(self):         # Mark all the vertices as not visited         visited = [False]*self.V         stack =[]          # Call the recursive helper function to store Topological         # Sort starting from all vertices one by one         for i in range(self.V):             if visited[i] == False:                 self.topologicalSortUtil(i,visited,stack)          # Print contents of stack         print (stack)  g= Graph(6) g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1);  print ("Following is a Topological Sort of the given graph") g.topologicalSort()

Output

Following is a Topological Sort of the given graph [5, 4, 2, 3, 1, 0]

Iterative DFS-Based Topological Sorting

This method eliminates recursion and uses an explicit stack to simulate DFS traversal. It employs generators for efficient neighbor iteration and manually manages backtracking. This approach is useful for handling large graphs without hitting recursion limits.

Algorithm:

The way topological sorting is solved is by processing a node after all of its children are processed. Each time a node is processed, it is pushed onto a stack in order to save the final result. This non-recursive solution builds on the same concept of DFS with a little tweak which can be understood above and in this article.
However, unlike the recursive solution, which saves the order of the nodes in the stack after all the neighboring elements have been pushed to the program stack, this solution replaces the program stack with a working stack. If a node has a neighbor that has not been visited, the current node and the neighbor are pushed to the working stack to be processed until there are no more neighbors available to be visited.
After all the nodes have been visited, what remains is the final result which is found by printing the stack result in reverse.

Python

from collections import defaultdict  #Class to represent a graph class Graph:     def __init__(self,vertices):         self.graph = defaultdict(list) #dictionary containing adjacency List         self.V = vertices #No. of vertices      # function to add an edge to graph     def addEdge(self,u,v):         self.graph[u].append(v)      # neighbors generator given key     def neighbor_gen(self,v):         for k in self.graph[v]:             yield k          # non recursive topological sort     def nonRecursiveTopologicalSortUtil(self, v, visited,stack):                  # working stack contains key and the corresponding current generator         working_stack = [(v,self.neighbor_gen(v))]                  while working_stack:             # get last element from stack             v, gen = working_stack.pop()             visited[v] = True                          # run through neighbor generator until it's empty             for next_neighbor in gen:                 if not visited[next_neighbor]: # not seen before?                     # remember current work                     working_stack.append((v,gen))                     # restart with new neighbor                     working_stack.append((next_neighbor, self.neighbor_gen(next_neighbor)))                     break             else:                 # no already-visited neighbor (or no more of them)                 stack.append(v)                      # The function to do Topological Sort.     def nonRecursiveTopologicalSort(self):         # Mark all the vertices as not visited         visited = [False]*self.V                  # result stack         stack = []          # Call the helper function to store Topological         # Sort starting from all vertices one by one         for i in range(self.V):             if not(visited[i]):                 self.nonRecursiveTopologicalSortUtil(i, visited,stack)         # Print contents of the stack in reverse         stack.reverse()         print(stack)  g= Graph(6) g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1);  print("The following is a Topological Sort of the given graph") g.nonRecursiveTopologicalSort()

Output

The following is a Topological Sort of the given graph [5, 4, 2, 3, 1, 0]

Complexity Analysis:

Time Complexity: O(V + E): The above algorithm is simply DFS with a working stack and a result stack. Unlike the recursive solution, recursion depth is not an issue here.
Auxiliary space: O(V): The extra space is needed for the 2 stacks used.

Please refer complete article on Topological Sorting for more details.

All Topological Sorts of a Directed Acyclic Graph

kartik

Improve

Article Tags :

Practice Tags :

python

Topological Sorting in Python

Recursive DFS-Based Topological Sorting

Iterative DFS-Based Topological Sorting

Algorithm:

Complexity Analysis:

Similar Reads

Topological Sort in different languages

Problems based on Topological Sort