Puzzle - Ways to Reach Bottom Right in 6x6 Grid
Last Updated : 28 Dec, 2024
You begin in the top left corner of a 6x6 grid, and your objective is to move to the bottom right corner. There are just two directions you can move: right or down. Both diagonal and backward movements are prohibited. How many different ways are there to get from the start to the finish?
 Puzzle
PuzzleWe can solve this problem using two approaches:-
Approach 1 - Using Combinatorics:
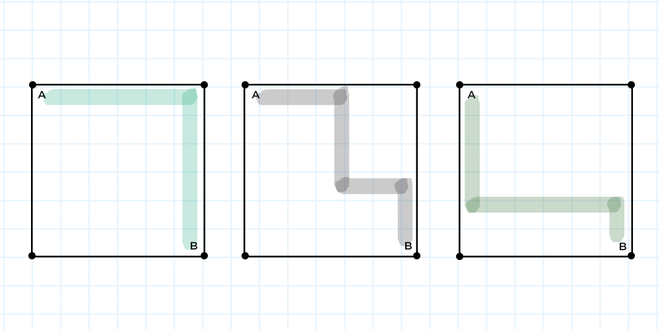 Three conditions of reaching at the last end
Three conditions of reaching at the last end Example of some ways to reach endpoint
Example of some ways to reach endpointWe can see here that the number of paths from starting left point to the right ending is not depending on the way of the path, it depends on the number of rows and columns taken to reach the end. Whenever we face such kind of problem, where we have a choice to take or a fixed number of rows or columns to be taken in grid. We can think about mathematics in those cases. Here, we are going to use a mathematical concept, called combinatorics.
Why combinatorics?
In this case of a 6×6 grid, all the paths must consist of a total of 10 moves, 5 down and 5 right, our job is to select the 5 right moves from the collection of 10 moves. we must employ a certain number of rows and columns (5 of the total 10 blocks) to travel from the left beginning to the right end.
if we choose 5 rows box then the answer is 10c5=252 and the same if we choose 5 column answer is 10c5=252.
Approach 2 - Using Pascal Triangle:
 Pascal Approach
Pascal ApproachIf we know the number of ways to reach the left box and an upper box of a given box, then, the number of ways to reach at the given box, we can easily visualize, it will be the sum of both because we can either reach here from the left box paths or upper box paths. As shown in the figure here, we can reach the left box in A ways and reach the upper blocks in B ways, so the total answer to reach will be A+B.

Here, for the first row, they can only be taken from the left move, not from the upward move. So the answer is 1 for the first row and similarly, for the first column they can be only taken from the upward move, not from the left move. So the answer here is also 1, and for the remaining grid, it is calculated using the Pascal Approach which is explained before. To reach the right endpoint, we have taken the sum of (126+126), which are moves at its top and left.
Practical Approach:
Visit https://www.geeksforgeeks.org/count-possible-paths-top-left-bottom-right-nxm-matrix/ to practice and have detailed solutions using recursion and dynamic programming.
Similar Reads
Puzzle | Can a Knight reach bottom from top by visiting all squares PuzzleIs there a way for a chess knight to start at the top-left corner from a N x N chessboard, visit all the squares of the board exactly once and end at the lower-right corner. SolutionWe need to traverse all the squares of the chessboard exactly once. Also, the moves of the knight are L-shaped,
2 min read
Count of Reachable cells in Grid within given Left-Right moves Given a grid of size N X M in which some cells are empty, and some have obstacles, the task is to find how many cells (including the starting cell) are reachable from cell (startRow, startCol) such that number of right moves allowed are R and number of left moves allowed are L. An obstacle and empty
12 min read
Minimum cost to reach the last cell of a grid with directions Given a 2D matrix grid[][] of size M X N, where each cell of the grid has a character denoting the next cell we should visit we are at the current cell. The character at any cell can be: 'R' which means go to the cell to the right. (i.e from grid[i][j] to grid[i][j + 1]) 'L' which means go to the ce
12 min read
Minimum Cost to reach the end of the matrix Given a matrix of size N X N, such that each cell has an Uppercase Character in it, find the minimum cost to reach the cell (N-1, N-1) starting from (0, 0). From a cell (i, j), we can move Up(i-1, j), Down(i+1, j), Left (i, j-1) and Right(i, j+1). If the adjacent cell has the same character as the c
13 min read
Count paths with maximum sum from top-left to bottom-right cell (Adventure in a Maze) Given a 2D grid maze[][] of size N * N containing numbers 1, 2 or 3 where 1: means we can go Right from that cell only, 2 means we can go Down from that cell only and 3 means we can go Right and Down to both paths from that cell. We cannot go out of the maze at any time. Find the total number of pat
14 min read