Post Order Traversal of Binary Tree in O(N) using O(1) space
Last Updated : 03 Jun, 2024
Prerequisites:- Morris Inorder Traversal, Tree Traversals (Inorder, Preorder and Postorder)
Given a Binary Tree, the task is to print the elements in post order using O(N) time complexity and constant space.
Input: 1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
Output: 8 9 4 5 2 6 7 3 1
Input: 5
/ \
7 3
/ \ / \
4 11 13 9
/ \
8 4
Output: 8 4 4 11 7 13 9 3 5
Method 1: Using Morris Inorder Traversal
- Create a dummy node and make the root as it's left child.
- Initialize current with dummy node.
- While current is not NULL
- If the current does not have a left child traverse the right child, current = current->right
- Otherwise,
- Find the rightmost child in the left subtree.
- If rightmost child's right child is NULL
- Make current as the right child of the rightmost node.
- Traverse the left child, current = current->left
- Otherwise,
- Set the rightmost child's right pointer to NULL.
- From current's left child, traverse along with the right children until the rightmost child and reverse the pointers.
- Traverse back from rightmost child to current's left child node by reversing the pointers and printing the elements.
- Traverse the right child, current = current->right
Below is the diagram showing the rightmost child in the left subtree, pointing to its inorder successor.
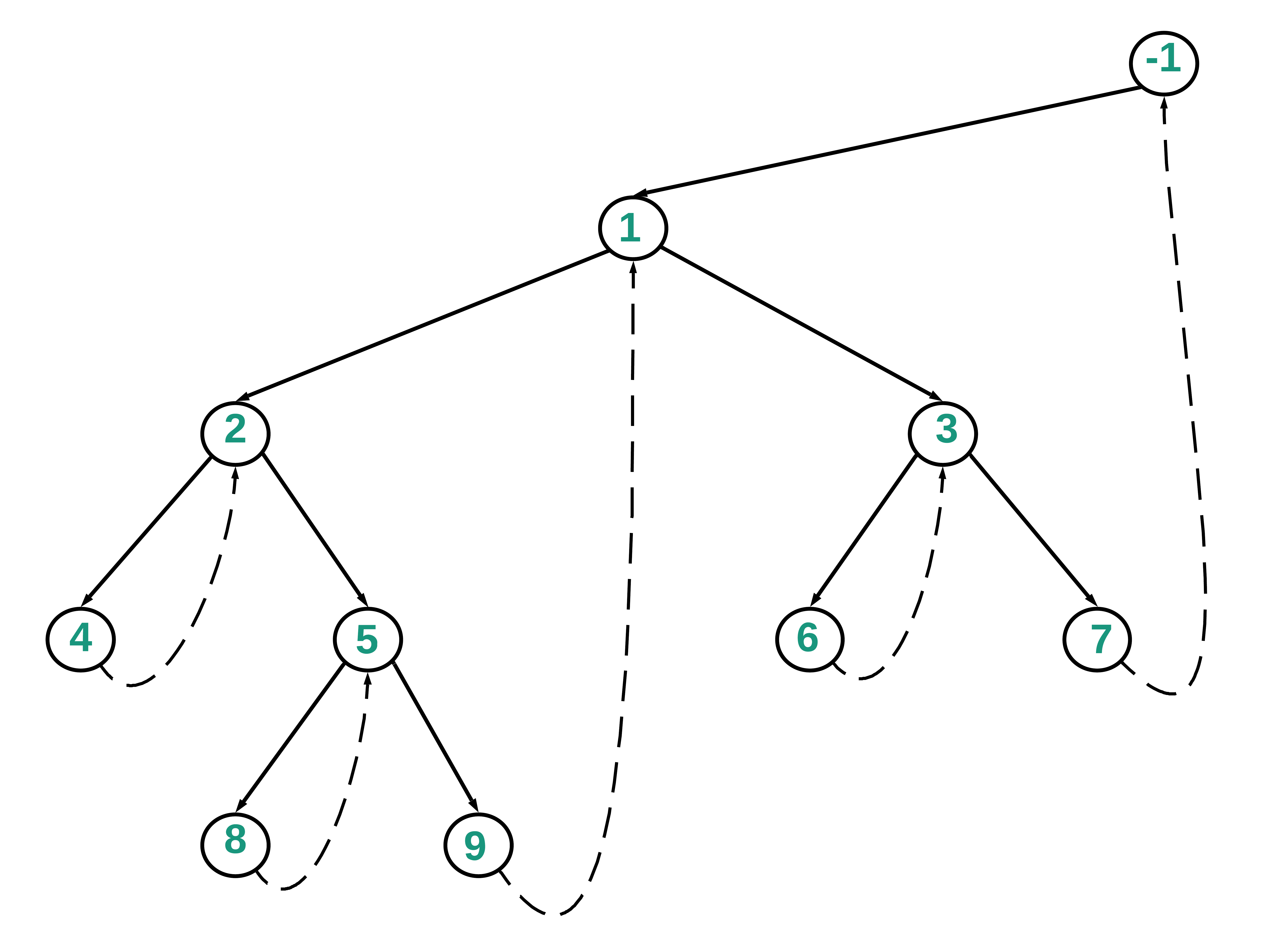
Below is the diagram which highlights the path 1->2->5->9 and the way the nodes are processed and printed as per the above algorithm.

Below is the implementation of the above approach:
C++ // C++ program to implement // Post Order traversal // of Binary Tree in O(N) // time and O(1) space #include <bits/stdc++.h> using namespace std; class node { public: int data; node *left, *right; }; // Helper function that allocates a // new node with the given data and // NULL left and right pointers. node* newNode(int data) { node* temp = new node(); temp->data = data; temp->left = temp->right = NULL; return temp; } // Postorder traversal without recursion // and without stack void postOrderConstSpace(node* root) { if (root == NULL) return; node* current = newNode(-1); node* pre = NULL; node* prev = NULL; node* succ = NULL; node* temp = NULL; current->left = root; while (current) { // If left child is null. // Move to right child. if (current->left == NULL) { current = current->right; } else { pre = current->left; // Inorder predecessor while (pre->right && pre->right != current) pre = pre->right; // The connection between current and // predecessor is made if (pre->right == NULL) { // Make current as the right // child of the right most node pre->right = current; // Traverse the left child current = current->left; } else { pre->right = NULL; succ = current; current = current->left; prev = NULL; // Traverse along the right // subtree to the // right-most child while (current != NULL) { temp = current->right; current->right = prev; prev = current; current = temp; } // Traverse back // to current's left child // node while (prev != NULL) { cout << prev->data << " "; temp = prev->right; prev->right = current; current = prev; prev = temp; } current = succ; current = current->right; } } } } // Driver code int main() { /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ node* root = NULL; root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); root->right->left = newNode(6); root->right->right = newNode(7); root->left->right->left = newNode(8); root->left->right->right = newNode(9); postOrderConstSpace(root); return 0; } // This code is contributed by Saurav Chaudhary // Java program to implement // Post Order traversal // of Binary Tree in O(N) // time and O(1) space // Definition of the // binary tree class TreeNode { public int data; public TreeNode left; public TreeNode right; public TreeNode(int data) { this.data = data; } public String toString() { return data + " "; } } public class PostOrder { TreeNode root; // Function to find Post Order // Traversal Using Constant space void postOrderConstantspace(TreeNode root) { if (root == null) return; TreeNode current = new TreeNode(-1), pre = null; TreeNode prev = null, succ = null, temp = null; current.left = root; while (current != null) { // Go to the right child // if current does not // have a left child if (current.left == null) { current = current.right; } else { // Traverse left child pre = current.left; // Find the right most child // in the left subtree while (pre.right != null && pre.right != current) pre = pre.right; if (pre.right == null) { // Make current as the right // child of the right most node pre.right = current; // Traverse the left child current = current.left; } else { pre.right = null; succ = current; current = current.left; prev = null; // Traverse along the right // subtree to the // right-most child while (current != null) { temp = current.right; current.right = prev; prev = current; current = temp; } // Traverse back from // right most child to // current's left child node while (prev != null) { System.out.print(prev); temp = prev.right; prev.right = current; current = prev; prev = temp; } current = succ; current = current.right; } } } } // Driver Code public static void main(String[] args) { /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ PostOrder tree = new PostOrder(); tree.root = new TreeNode(1); tree.root.left = new TreeNode(2); tree.root.right = new TreeNode(3); tree.root.left.left = new TreeNode(4); tree.root.left.right = new TreeNode(5); tree.root.right.left = new TreeNode(6); tree.root.right.right = new TreeNode(7); tree.root.left.right.left = new TreeNode(8); tree.root.left.right.right = new TreeNode(9); tree.postOrderConstantspace( tree.root); } } # Python3 program to implement # Post Order traversal # of Binary Tree in O(N) # time and O(1) space class node: def __init__(self, data): self.data = data self.left = None self.right = None # Helper function that allocates a # new node with the given data and # None left and right pointers. def newNode(data): temp = node(data) return temp # Postorder traversal without recursion # and without stack def postOrderConstSpace(root): if (root == None): return current = newNode(-1) pre = None prev = None succ = None temp = None current.left = root while (current): # If left child is None. # Move to right child. if (current.left == None): current = current.right else: pre = current.left # Inorder predecessor while (pre.right and pre.right != current): pre = pre.right # The connection between current # and predecessor is made if (pre.right == None): # Make current as the right # child of the right most node pre.right = current # Traverse the left child current = current.left else: pre.right = None succ = current current = current.left prev = None # Traverse along the right # subtree to the # right-most child while (current != None): temp = current.right current.right = prev prev = current current = temp # Traverse back # to current's left child # node while (prev != None): print(prev.data, end = ' ') temp = prev.right prev.right = current current = prev prev = temp current = succ current = current.right # Driver code if __name__=='__main__': ''' Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 ''' root = None root = newNode(1) root.left = newNode(2) root.right = newNode(3) root.left.left = newNode(4) root.left.right = newNode(5) root.right.left = newNode(6) root.right.right = newNode(7) root.left.right.left = newNode(8) root.left.right.right = newNode(9) postOrderConstSpace(root) # This code is contributed by pratham76
// C# program to implement // Post Order traversal // of Binary Tree in O(N) // time and O(1) space using System; // Definition of the // binary tree public class TreeNode { public int data; public TreeNode left, right; public TreeNode(int item) { data = item; left = right = null; } } class PostOrder{ public TreeNode root; // Function to find Post Order // Traversal Using Constant space void postOrderConstantspace(TreeNode root) { if (root == null) return; TreeNode current = new TreeNode(-1), pre = null; TreeNode prev = null, succ = null, temp = null; current.left = root; while (current != null) { // Go to the right child // if current does not // have a left child if (current.left == null) { current = current.right; } else { // Traverse left child pre = current.left; // Find the right most child // in the left subtree while (pre.right != null && pre.right != current) pre = pre.right; if (pre.right == null) { // Make current as the right // child of the right most node pre.right = current; // Traverse the left child current = current.left; } else { pre.right = null; succ = current; current = current.left; prev = null; // Traverse along the right // subtree to the // right-most child while (current != null) { temp = current.right; current.right = prev; prev = current; current = temp; } // Traverse back from // right most child to // current's left child node while (prev != null) { Console.Write(prev.data + " "); temp = prev.right; prev.right = current; current = prev; prev = temp; } current = succ; current = current.right; } } } } // Driver code static public void Main () { /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ PostOrder tree = new PostOrder(); tree.root = new TreeNode(1); tree.root.left = new TreeNode(2); tree.root.right = new TreeNode(3); tree.root.left.left = new TreeNode(4); tree.root.left.right = new TreeNode(5); tree.root.right.left = new TreeNode(6); tree.root.right.right = new TreeNode(7); tree.root.left.right.left = new TreeNode(8); tree.root.left.right.right = new TreeNode(9); tree.postOrderConstantspace(tree.root); } } // This code is contributed by offbeat <script> // Javascript program to implement // Post Order traversal // of Binary Tree in O(N) // time and O(1) space // Definition of the // binary tree class TreeNode { constructor(item) { this.data = item; this.left = null; this.right = null; } } var root; // Function to find Post Order // Traversal Using Constant space function postOrderConstantspace(root) { if (root == null) return; var current = new TreeNode(-1), pre = null; var prev = null, succ = null, temp = null; current.left = root; while (current != null) { // Go to the right child // if current does not // have a left child if (current.left == null) { current = current.right; } else { // Traverse left child pre = current.left; // Find the right most child // in the left subtree while (pre.right != null && pre.right != current) pre = pre.right; if (pre.right == null) { // Make current as the right // child of the right most node pre.right = current; // Traverse the left child current = current.left; } else { pre.right = null; succ = current; current = current.left; prev = null; // Traverse along the right // subtree to the // right-most child while (current != null) { temp = current.right; current.right = prev; prev = current; current = temp; } // Traverse back from // right most child to // current's left child node while (prev != null) { document.write(prev.data + " "); temp = prev.right; prev.right = current; current = prev; prev = temp; } current = succ; current = current.right; } } } } // Driver code /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ var tree = new TreeNode(); tree.root = new TreeNode(1); tree.root.left = new TreeNode(2); tree.root.right = new TreeNode(3); tree.root.left.left = new TreeNode(4); tree.root.left.right = new TreeNode(5); tree.root.right.left = new TreeNode(6); tree.root.right.right = new TreeNode(7); tree.root.left.right.left = new TreeNode(8); tree.root.left.right.right = new TreeNode(9); postOrderConstantspace(tree.root); </script> Time Complexity: O(N)
Auxiliary Space: O(1)
Method 2: In method 1, we traverse a path, reverse references, print nodes as we restore the references by reversing them again. In method 2, instead of reversing paths and restoring the structure, we traverse to the parent node from the current node using the current node's left subtree. This could be faster depending on the tree structure, for example in a right-skewed tree.
The following algorithm and diagrams provide the details of the approach.

Below is the conceptual diagram showing how the left and right child references are used to traverse back and forth.
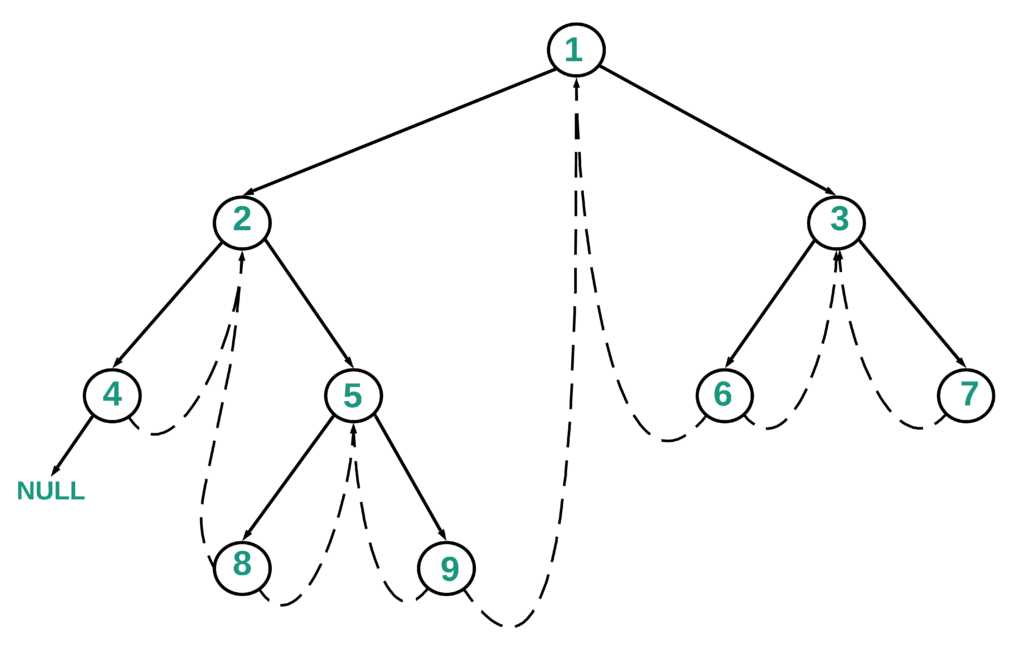
Below is the diagram which highlights the path 1->2->5->9 and the way the nodes are processed and printed as per the above algorithm.
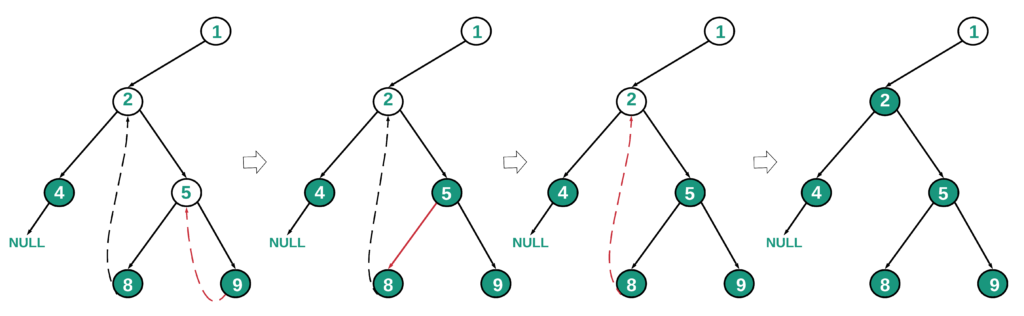
Below is the implementation of the above approach:
C++ // C++ Program to implement the above approach #include <bits/stdc++.h> using namespace std; struct TreeNode { TreeNode* left; TreeNode* right; int data; TreeNode(int data) { this->data = data; this->left = nullptr; this->right = nullptr; } }; TreeNode* root; // Function to Calculate Post // Order Traversal Using // Constant Space static void postOrderConstantspace(TreeNode* root) { if (root == nullptr) return; TreeNode* current = nullptr; TreeNode* prevNode = nullptr; TreeNode* pre = nullptr; TreeNode* ptr = nullptr; TreeNode* netChild = nullptr; TreeNode* prevPtr = nullptr; current = root; while (current != nullptr) { if (current->left == nullptr) { current->left = prevNode; // Set prevNode to current prevNode = current; current = current->right; } else { pre = current->left; // Find the right most child // in the left subtree while (pre->right != nullptr && pre->right != current) pre = pre->right; if (pre->right == nullptr) { pre->right = current; current = current->left; } else { // Set the right most // child's right pointer // to NULL pre->right = nullptr; cout << pre->data << " "; ptr = pre; netChild = pre; prevPtr = pre; while (ptr != nullptr) { if (ptr->right == netChild) { cout << ptr->data << " "; netChild = ptr; prevPtr->left = nullptr; } if (ptr == current->left) break; // Break the loop // all the left subtree // nodes of current // processed prevPtr = ptr; ptr = ptr->left; } prevNode = current; current = current->right; } } } cout << prevNode->data << " "; // Last path traversal // that includes the root. ptr = prevNode; netChild = prevNode; prevPtr = prevNode; while (ptr != nullptr) { if (ptr->right == netChild) { cout << ptr->data << " "; netChild = ptr; prevPtr->left = nullptr; } if (ptr == root) break; prevPtr = ptr; ptr = ptr->left; } } int main() { /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->left->right = new TreeNode(5); root->right->left = new TreeNode(6); root->right->right = new TreeNode(7); root->left->right->left = new TreeNode(8); root->left->right->right = new TreeNode(9); postOrderConstantspace(root); return 0; } // This code is contributed by mukesh07. // Java Program to implement // the above approach class TreeNode { public int data; public TreeNode left; public TreeNode right; public TreeNode(int data) { this.data = data; } public String toString() { return data + " "; } } public class PostOrder { TreeNode root; // Function to Calculate Post // Order Traversal // Using Constant Space void postOrderConstantspace(TreeNode root) { if (root == null) return; TreeNode current = null; TreeNode prevNode = null; TreeNode pre = null; TreeNode ptr = null; TreeNode netChild = null; TreeNode prevPtr = null; current = root; while (current != null) { if (current.left == null) { current.left = prevNode; // Set prevNode to current prevNode = current; current = current.right; } else { pre = current.left; // Find the right most child // in the left subtree while (pre.right != null && pre.right != current) pre = pre.right; if (pre.right == null) { pre.right = current; current = current.left; } else { // Set the right most // child's right pointer // to NULL pre.right = null; System.out.print(pre); ptr = pre; netChild = pre; prevPtr = pre; while (ptr != null) { if (ptr.right == netChild) { System.out.print(ptr); netChild = ptr; prevPtr.left = null; } if (ptr == current.left) break; // Break the loop // all the left subtree // nodes of current // processed prevPtr = ptr; ptr = ptr.left; } prevNode = current; current = current.right; } } } System.out.print(prevNode); // Last path traversal // that includes the root. ptr = prevNode; netChild = prevNode; prevPtr = prevNode; while (ptr != null) { if (ptr.right == netChild) { System.out.print(ptr); netChild = ptr; prevPtr.left = null; } if (ptr == root) break; prevPtr = ptr; ptr = ptr.left; } } // Main Function public static void main(String[] args) { /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ PostOrder tree = new PostOrder(); tree.root = new TreeNode(1); tree.root.left = new TreeNode(2); tree.root.right = new TreeNode(3); tree.root.left.left = new TreeNode(4); tree.root.left.right = new TreeNode(5); tree.root.right.left = new TreeNode(6); tree.root.right.right = new TreeNode(7); tree.root.left.right.left = new TreeNode(8); tree.root.left.right.right = new TreeNode(9); tree.postOrderConstantspace( tree.root); } } # Python3 Program to implement the above approach class TreeNode: def __init__(self, data): self.data = data self.left = None self.right = None # Function to Calculate Post # Order Traversal Using # Constant Space def postOrderConstantspace(root): if root == None: return current = None prevNode = None pre = None ptr = None netChild = None prevPtr = None current = root while current != None: if current.left == None: current.left = prevNode # Set prevNode to current prevNode = current current = current.right else: pre = current.left # Find the right most child # in the left subtree while pre.right != None and pre.right != current: pre = pre.right if pre.right == None: pre.right = current current = current.left else: # Set the right most # child's right pointer # to NULL pre.right = None print(pre.data, end = " ") ptr = pre netChild = pre prevPtr = pre while ptr != None: if ptr.right == netChild: print(ptr.data, end = " ") netChild = ptr prevPtr.left = None if ptr == current.left: break # Break the loop # all the left subtree # nodes of current # processed prevPtr = ptr ptr = ptr.left prevNode = current current = current.right print(prevNode.data, end = " ") # Last path traversal # that includes the root. ptr = prevNode netChild = prevNode prevPtr = prevNode while ptr != None: if ptr.right == netChild: print(ptr.data, end = " ") netChild = ptr prevPtr.left = None if (ptr == root): break prevPtr = ptr ptr = ptr.left """ Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 """ root = TreeNode(1) root.left = TreeNode(2) root.right = TreeNode(3) root.left.left = TreeNode(4) root.left.right = TreeNode(5) root.right.left = TreeNode(6) root.right.right = TreeNode(7) root.left.right.left = TreeNode(8) root.left.right.right = TreeNode(9) postOrderConstantspace(root) # This code is contributed by divyeshrabadiya07.
// C# Program to implement // the above approach using System; class TreeNode{ public int data; public TreeNode left; public TreeNode right; public TreeNode(int data) { this.data = data; } public string toString() { return data + " "; } } class PostOrder{ TreeNode root; // Function to Calculate Post // Order Traversal Using // Constant Space void postOrderConstantspace(TreeNode root) { if (root == null) return; TreeNode current = null; TreeNode prevNode = null; TreeNode pre = null; TreeNode ptr = null; TreeNode netChild = null; TreeNode prevPtr = null; current = root; while (current != null) { if (current.left == null) { current.left = prevNode; // Set prevNode to current prevNode = current; current = current.right; } else { pre = current.left; // Find the right most child // in the left subtree while (pre.right != null && pre.right != current) pre = pre.right; if (pre.right == null) { pre.right = current; current = current.left; } else { // Set the right most // child's right pointer // to NULL pre.right = null; Console.Write(pre.data + " "); ptr = pre; netChild = pre; prevPtr = pre; while (ptr != null) { if (ptr.right == netChild) { Console.Write(ptr.data + " "); netChild = ptr; prevPtr.left = null; } if (ptr == current.left) break; // Break the loop // all the left subtree // nodes of current // processed prevPtr = ptr; ptr = ptr.left; } prevNode = current; current = current.right; } } } Console.Write(prevNode.data + " "); // Last path traversal // that includes the root. ptr = prevNode; netChild = prevNode; prevPtr = prevNode; while (ptr != null) { if (ptr.right == netChild) { Console.Write(ptr.data + " "); netChild = ptr; prevPtr.left = null; } if (ptr == root) break; prevPtr = ptr; ptr = ptr.left; } } // Driver code public static void Main(string[] args) { /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ PostOrder tree = new PostOrder(); tree.root = new TreeNode(1); tree.root.left = new TreeNode(2); tree.root.right = new TreeNode(3); tree.root.left.left = new TreeNode(4); tree.root.left.right = new TreeNode(5); tree.root.right.left = new TreeNode(6); tree.root.right.right = new TreeNode(7); tree.root.left.right.left = new TreeNode(8); tree.root.left.right.right = new TreeNode(9); tree.postOrderConstantspace(tree.root); } } // This code is contributed by Rutvik_56 <script> // Javascript Program to implement the above approach class TreeNode { constructor(data) { this.left = null; this.right = null; this.data = data; } } let root; // Function to Calculate Post // Order Traversal Using // Constant Space function postOrderConstantspace(root) { if (root == null) return; let current = null; let prevNode = null; let pre = null; let ptr = null; let netChild = null; let prevPtr = null; current = root; while (current != null) { if (current.left == null) { current.left = prevNode; // Set prevNode to current prevNode = current; current = current.right; } else { pre = current.left; // Find the right most child // in the left subtree while (pre.right != null && pre.right != current) pre = pre.right; if (pre.right == null) { pre.right = current; current = current.left; } else { // Set the right most // child's right pointer // to NULL pre.right = null; document.write(pre.data + " "); ptr = pre; netChild = pre; prevPtr = pre; while (ptr != null) { if (ptr.right == netChild) { document.write(ptr.data + " "); netChild = ptr; prevPtr.left = null; } if (ptr == current.left) break; // Break the loop // all the left subtree // nodes of current // processed prevPtr = ptr; ptr = ptr.left; } prevNode = current; current = current.right; } } } document.write(prevNode.data + " "); // Last path traversal // that includes the root. ptr = prevNode; netChild = prevNode; prevPtr = prevNode; while (ptr != null) { if (ptr.right == netChild) { document.write(ptr.data + " "); netChild = ptr; prevPtr.left = null; } if (ptr == root) break; prevPtr = ptr; ptr = ptr.left; } } /* Constructed tree is as follows:- 1 / \ 2 3 / \ / \ 4 5 6 7 / \ 8 9 */ root = new TreeNode(1); root.left = new TreeNode(2); root.right = new TreeNode(3); root.left.left = new TreeNode(4); root.left.right = new TreeNode(5); root.right.left = new TreeNode(6); root.right.right = new TreeNode(7); root.left.right.left = new TreeNode(8); root.left.right.right = new TreeNode(9); postOrderConstantspace(root); // This code is contributed by divyesh072019. </script> Time Complexity: O(N)
Auxiliary Space: O(1)
Similar Reads
Find n-th node in Preorder traversal of a Binary Tree
Given a binary tree. The task is to find the n-th node of preorder traversal. Examples: Input: Output: 50Explanation: Preorder Traversal is: 10 20 40 50 30 and value of 4th node is 50.Input: Output : 3Explanation: Preorder Traversal is: 7 2 3 8 5 and value of 3rd node is 3. Table of Content [Naive A
11 min read
Level order traversal of Binary Tree using Morris Traversal
Given a binary tree, the task is to traverse the Binary Tree in level order fashion.Examples: Input: 1 / \ 2 3 Output: 1 2 3 Input: 5 / \ 2 3 \ 6 Output: 5 2 3 6 Approach: The idea is to use Morris Preorder Traversal to traverse the tree in level order traversal.Observations: There are mainly two ob
11 min read
Flatten binary tree in order of post-order traversal
Given a binary tree, the task is to flatten it in order of its post-order traversal. In the flattened binary tree, the left node of all the nodes must be NULL. Examples: Input: 5 / \ 3 7 / \ / \ 2 4 6 8 Output: 2 4 3 6 8 7 5 Input: 1 \ 2 \ 3 \ 4 \ 5 Output: 5 4 3 2 1 A simple approach will be to rec
7 min read
Pre Order, Post Order and In Order traversal of a Binary Tree in one traversal | (Using recursion)
Given a binary tree, the task is to print all the nodes of the binary tree in Pre-order, Post-order, and In-order in one iteration. Examples: Input: Output: Pre Order: 1 2 4 5 3 6 7 Post Order: 4 5 2 6 7 3 1 In Order: 4 2 5 1 6 3 7 Input: Output: Pre Order: 1 2 4 8 12 5 9 3 6 7 10 11 Post Order: 12
9 min read
Mix Order Traversal of a Binary Tree
Given a Binary Tree consisting of N nodes, the task is to print its Mix Order Traversal. Mix Order Traversal is a tree traversal technique, which involves any two of the existing traversal techniques like Inorder, Preorder and Postorder Traversal. Any two of them can be performed or alternate levels
13 min read
Middle To Up-Down Order traversal of a Binary Tree
Given a binary tree, the task is to traverse this binary tree from the middle to the up-down order. In Middle to up-down order traversal, the following steps are performed: First, print the middle level of the tree.Then, print the elements at one level above the middle level of the tree.Then, print
15+ min read
Find all possible Binary Trees with given Inorder Traversal
Given an array that represents Inorder Traversal, the task is to find all possible Binary Trees with the given inorder traversal and print their preorder traversals. Examples: Input: inorder[] = {7, 5}Output: 5 77 5 Input: inorder[] = {1, 2, 3}Output: 1 2 31 3 22 1 33 1 23 2 1 Approach: The idea is
8 min read
Inorder Traversal of Binary Tree
Inorder traversal is a depth-first traversal method that follows this sequence: Left subtree is visited first.Root node is processed next.Right subtree is visited last.How does Inorder Traversal work? Key Properties:If applied to a Binary Search Tree (BST), it returns elements in sorted order.Ensure
5 min read
Double Order Traversal of a Binary Tree
Given a Binary Tree, the task is to find its Double Order Traversal. Double Order Traversal is a tree traversal technique in which every node is traversed twice in the following order: Visit the Node.Traverse the Left Subtree.Visit the Node.Traverse the Right Subtree.Examples: Input: Output: 1 7 4 4
6 min read
Triple Order Traversal of a Binary Tree
Given a Binary Tree, the task is to find its Triple Order Traversal. Triple Order Traversal is a tree traversal technique in which every node is traversed thrice in the following order: Visit the root nodeTraverse the left subtreeVisit the root nodeTraverse the right subtreeVisit the root node.Examp
7 min read