Skip to content
geeksforgeeks
  • Tutorials
    • Python
    • Java
    • Data Structures & Algorithms
    • ML & Data Science
    • Interview Corner
    • Programming Languages
    • Web Development
    • CS Subjects
    • DevOps And Linux
    • School Learning
    • Practice Coding Problems
  • Courses
    • DSA to Development
    • Get IBM Certification
    • Newly Launched!
      • Master Django Framework
      • Become AWS Certified
    • For Working Professionals
      • Interview 101: DSA & System Design
      • Data Science Training Program
      • JAVA Backend Development (Live)
      • DevOps Engineering (LIVE)
      • Data Structures & Algorithms in Python
    • For Students
      • Placement Preparation Course
      • Data Science (Live)
      • Data Structure & Algorithm-Self Paced (C++/JAVA)
      • Master Competitive Programming (Live)
      • Full Stack Development with React & Node JS (Live)
    • Full Stack Development
    • Data Science Program
    • All Courses
  • Physics
  • CBSE Physics Class 8 Notes
  • CBSE Class 9 Physics Notes
  • CBSE Notes for Class 10 Physics
  • CBSE Class 11 Physics Notes
  • CBSE Class 12 Physics Notes
  • CBSE Class 8 Science Notes
  • CBSE Class 9 Science Notes
  • Class 10 Science Notes
Open In App
Next Article:
Simple Harmonic Motion
Next article icon

Energy of a Wave Formula

Last Updated : 03 May, 2024
Comments
Improve
Suggest changes
Like Article
Like
Report

Wave energy, often referred to as the energy carried by waves, encompasses both the kinetic energy of their motion and the potential energy stored within their amplitude or frequency. This energy is not only essential for natural processes like ocean currents and seismic waves but also holds significant promise for renewable energy generation.

Table of Content

  • Energy
  • Wave
  • The Relationship Between Wave Energy and Amplitude
  • Formula for the Energy of a Wave 
  • Sample Problems

Energy

Physics defines the capability of doing work as a concept called energy. Energy also follows the law of conservation that is "energy cannot be created and can not be destroyed". Heat, light, and sound all are forms of energy. Energy also follows some rule to move from one body to another. 

Whenever energy has been transferred, it is always designated according to its nature. This states that energy always changes its form if required like electric energy got converted into light when a bulb is lightened, similarly wind energy can be converted to mechanical and then electrical in windmills. 

Also Check: Energy

Wave

A wave is a disturbance/ movement of particles in a medium that transports energy without causing net particle movement. Elastic deformation, pressure variations, electric or magnetic field, electronic potential, or temperature variations are all examples.

Check: Introduction to Waves

The Relationship Between Wave Energy and Amplitude

  • The relationship between wave energy and amplitude is crucial for understanding wave behavior.
  • Amplitude refers to the maximum displacement or intensity of a wave.
  • It represents the height of a wave from its crest to its trough.
  • Wave energy encompasses both kinetic and potential energy carried by a wave.
  • Greater amplitudes result in waves carrying more energy.
  • Understanding this relationship aids in predicting and manipulating wave behavior for various applications.
  • Applications include earthquake monitoring, ocean wave energy conversion, and telecommunications.
  • Studying changes in amplitude provides insights into optimizing technologies and harnessing wave power effectively.

Formula for the Energy of a Wave 

  • When matter oscillates, it transfers energy through a medium, forming mechanical waves.
  • These waves can travel long distances while keeping the medium stationary.
  • Energy is carried by both mechanical and electromagnetic waves, flowing in the same direction as the waves.
  • The energy of a wave is determined by its amplitude and frequency.
  • Large-amplitude earthquakes result in significant ground displacements.
  • Loud sounds have high-pressure amplitudes, originating from larger-amplitude source vibrations than softer sounds.
  • High-frequency waves deliver more energy packets per unit of time compared to low-frequency waves.
  • If two mechanical waves have equal amplitudes but one has twice the frequency of the other, the higher-frequency wave transfers energy at a rate four times greater.

The main components of wave energy are Kinetic energy and Potential energy.

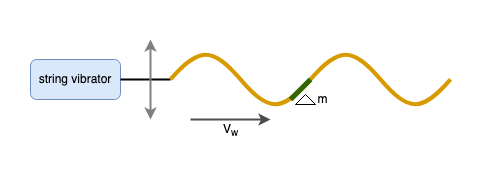A string is attached to the rod of the string vibrator, which produces a sinusoidal wave in the string, with a wave velocity v. A section of the string with mass Δm oscillates at the same frequency as the wave.
  • Kinetic Energy Component

The Formula of Kinetic energy is,

Ukinetic = mv2 / 2 

Let v be the velocity of the wave.

Since, velocity has two component vx (horizontal component in direction of motion of wave) and vy (perpendicular component perpendicular to motion of wave).

So, the kinetic energy of each mass element of the string is, 

ΔUkinetic = 1/2 (Δm) vy2

as the mass element oscillates perpendicular to the direction of the motion of the wave. 

If the density of string is μ, then the mass of element (Δx) of string, 

Δm = μΔx

Hence, Kinetic energy is:

ΔUkinetic = 1/2 (μΔx)vy2

For total kinetic energy of wave we have,

Ukinetic = 1/4(μA2ω2λ)

where A is the amplitude of the wave (in metres), ω is the angular frequency of the wave oscillator (in Hertz), λ is the wavelength (in metres).

  • Potential Energy Component

In Oscillations, the potential energy stored in a spring with a linear restoring force is,

U = 1/2ksx2

where the equilibrium position is defined at x = 0 m.

The potential energy of the mass element is,

U = 1/2ksx2 

= 1/2 Δmw2x2

= 1/4 (μA2ω2λ)

where A is the amplitude of the wave (in metres), ω is the angular frequency of the wave oscillator(in hertz), λ is the wavelength (in metres).

  • Hence, the Total Wave Energy

Utotal = Upotential + Ukinetic

=  1/4(μA2ω2λ) + 1/4(μA2ω2λ)

Utotal  =  1/2(μA2ω2λ)

where A is the amplitude of the wave (in metres), ω the angular frequency of the wave oscillator(in hertz), and λ the wavelength (in metres).

Related Article

  • What is a Wave?
  • Light Energy
  • Wave Motion
  • Properties of Waves
  • Types of Waves

Sample Problems

Problem 1: For a wave with given values, amplitude A = 10 m, angular frequency, ω = 50 Hz, wavelength λ = 10 m, and string density μ = 200. Find the wave energy by using Wave Energy Formula.

Solution: 

Utotal = 1/2 (200 × 10 × 10 × 50 × 50 × 10)

= 2500000 J

= 2.5 MJ

Problem 2: Describe the components of wave energy.

Solution: 

Wave energy has two components kinetic energy of wave particles and potential energy. 

Wave energy, U = Upotential + Ukinetic = 1/4(μA2ω2λ) + 1/4(μA2ω2λ) =  1/2(μA2ω2λ)

where A is the amplitude of the wave (in meters), ω the angular frequency of the wave oscillator (in Hertz), and λ the wavelength (in meters).

Problem 3: With what factor should the amplitude be increased, increase the intensity of a wave by a factor of 64?

Solution: 

Since, according to the Wave energy formula, the intensity of a wave is directly proportional to the square of the amplitude of the wave.

So, the relation can be written as:   

I ∝ X2

Here I is the intensity and X is the amplitude.

To increase the intensity by a factor of 64 we need to increase the amplitude by a factor of (64)1/2  which is equal to 8.

Problem 4: With what factor should the intensity of a wave be increased, increase amplitude by a factor 5?

Solution: 

Since, according to the Wave energy formula, the intensity of a wave is directly proportional to the square of the amplitude of the wave.

X2  ∝ I 

Here I is the intensity and X is the amplitude.

To increase amplitude by a factor of 5 we need to increase the intensity by a factor of (5)2 which is equal to 25.

Problem 5: Find the Amplitude of a wave of 0.5 J of energy with, ω = 1 Hz, λ = 1 m, and μ = 1.

Solution: 

Using wave energy formula :

Utotal = 1/2(μA2ω2λ))

0.5 J = 1/2 (1 × A2 × 12 × 1) J

A2 = 1 m2 

or

A = 1 m

Problem 6: Find the wavelength of a wave of 16 J of energy with, ω = 1 Hz, A (amplitude) = 1 m, and μ = 2.

Solution: 

Using wave energy formula :

Utotal = 1/2(μA2ω2λ))

16 J = 1/2 (2 × 12 × 12 × λ) J

λ = 16 m


Next Article
Simple Harmonic Motion

D
drananyashubhi
Improve
Article Tags :
  • School Learning
  • Physics
  • Physics-MAQ
  • Physics-Formulas
  • Physics-Concepts

Similar Reads

    Physics: Definition, Key Topics , Branches, Curriculum & Interesting Facts
    The term "physics" is derived from the Greek word physis (meaning “nature”) and physika (meaning “natural things”). It is the study of matter, energy, and the fundamental forces of nature, seeking to understand the behaviour of the universe from the smallest subatomic particles to the largest galaxi
    15+ min read

    Mechanics

    Rest and Motion
    Rest and motion describe the state of objects in relation to their surroundings. Whether an object is at rest or in motion, these states can be analyzed and understood through the principles of physics. When an object changes its position with respect to a stationary object with the passage of time,
    10 min read
    Force
    Force is defined as an external cause that a body experiences as a result of interacting with another body. Whenever two objects interact, a force is exerted on each object.  In general-term "To Push or Pull an Object" is defined as the force. The force is the interaction experience by the object be
    11 min read
    What is Pressure?
    Have you ever thought about why a needle is so thin, why fence spikes are pointed, or why a hammer's head is flat? It’s all about pressure. Pressure is the force applied to a specific area. A needle’s sharp tip concentrates the force, allowing it to easily pierce fabric. If it were blunt, the force
    7 min read
    Friction
    Friction in Physics is defined as a type of force that always opposes the motion of the object on which it is applied. Suppose we kick a football and it rolls for some distance and eventually it stops after rolling for some time. This is because of the friction force between the ball and the ground.
    8 min read
    Inertia Meaning
    Inertia is the basic concept of physics that is explained using the concept of Mass. The inertial concept was first explained by Sir Isaac Newton and the Law of Inertia is explained as any object in a state of rest or in a state of motion always staying in its state of rest or motion until an extern
    8 min read
    Newton's Laws of Motion | Formula, Examples and Questions
    Newton's Laws of Motion, formulated by the renowned English physicist Sir Isaac Newton, are fundamental principles that form the core of classical mechanics. These three laws explain how objects move and interact with forces, shaping our view of everything from everyday movement to the dynamics of c
    9 min read
    Universal Law of Gravitation
    Universal Law of Gravitation or Newton's law of Universal Gravitation as the name suggests is given by Sir Isaac Newton. This law helps us to understand the motion of very large bodies in the universe. According to this law, an attractive force always acts between two bodies that have masses. The st
    15 min read
    What is Gravity?
    There is a story about the discovery of gravity which says that Newton discovered gravity in the year 1665 when he was sitting under the apple tree, and suddenly an apple fell on his head, which led him to the question about falling objects. He questioned himself why all objects fall and also questi
    12 min read
    Law of Conservation of Energy
    Law of Conservation of Energy is the most fundamental law of physics which states that "Energy can neither be created nor be destroyed it can only change from one form of the energy to another form of the energy." It is the fundamental law of Physics that governs various processes in our environment
    11 min read
    Free Body Diagram
    Free Body Diagram often called FBD is a way of representing all the forces acting on a body at a particular instant in a simpler form. It enables the calculation of the net force acting on the body and its direction of motion by making a symbolic diagram of all the forces acting on a body. In this a
    10 min read
    Inclined Plane
    Inclined Plane is the most fundamental forms of mechanical devices used in physics. In order to get around physical obstacles and simplify tasks, inclined planes have been used for centuries in both ancient and recent construction projects. A flat surface that is angled with respect to the horizonta
    10 min read
    Work Done
    Work is said to be done when a force (push or pull) applied to an object causes a displacement of the object. In our daily life, we do work and get tired. Even if we are doing our work while sitting on a chair, we say we have done a lot of work and got tired. But this is not the work done as per the
    12 min read
    Conservative Forces - Definition, Formula, Examples
    Conservative Force is a type of force which is independent of path taken to do a work. This means when an when force applied in moving an object from one position to another is the same irrespective of the path taken, it is called conservative force. A force is a push or pull acting on an object. In
    7 min read
    Energy
    Energy in Physics is defined as the capacity of a body to do work. It is the capacity to complete a work. Energy can be broadly categorized into two categories, Kinetic Energy and Potential Energy. The capacity of an object to do the work is called the Energy. In this article, we will learn about, E
    10 min read
    Frame of Reference
    Frame of reference is a way to observe and measure objects' positions and movements. It acts like a coordinate system, helping us understand where things are and how they move. By using a frame of reference, we can describe motion accurately. It makes it clear if something is moving fast, slow, or a
    6 min read

    Kinematics

    Kinematics | Definition, Formula, Derivation, Problems
    Kinematics is the study of motion of points, objects, and systems by examining their motion from a geometric perspective, without focusing on the forces that cause such movements or the physical characteristics of the objects involved. This study area uses algebra to create mathematical models that
    10 min read
    What is Motion?
    Motion is defined as the change in the position of an object with respect to time i.e. when an object changes its position according to time it is said to be in the state of motion. Everything in the universe is in a state of continuous motion, for example, the moon revolves around the planets, the
    12 min read
    Distance and Displacement
    Distance and Displacement are two crucial terms of Mechanics that may seem the same but have different meanings and definitions. Distance is a measure of "How much path is covered by an object in motion?" While Displacement is the measure of "How much path is covered by the object in a particular di
    7 min read
    Speed and Velocity
    Mechanics can be termed as the branch of physics concerned with the concepts of energy and forces and their effect on bodies. It governs the relationships related to the motion of objects, that is, between matter, force, and its associated energy. It is responsible for the motion of bodies and the a
    13 min read
    Acceleration
    Acceleration is defined as the rate of change in velocity. This implies that if an object’s velocity is increasing or decreasing, then the object is accelerating. Acceleration has both magnitude and direction, therefore it is a Vector quantity. According to Newton's Second Law of Motion, acceleratio
    9 min read
    What is Momentum Equation?
    What is Momentum in Physics?The concept of Momentum in physics is very important, without which most of the theories in physics will fail. The momentum can be calculated by multiplying the mass of the substance and its velocity. In physics, momentum is of different types and forms. Let's know more a
    6 min read
    Equations of Motion: Derivations and Examples
    Equations of Motion was given by Sir Issac Newton; who is considered the father of mechanics. He was the first to give the fundamental physical laws that deal with objects and their motion. He formulated three equations of motion of an object and published them in his book Philosophiae Naturalis Pri
    11 min read
    Uniform Circular Motion
    Uniform Circular Motion as the name suggests, is the motion of a moving object with constant speed in a circular path. As we know, motion in a plane only has two coordinates, either x, and y, y and z, or z and x. Except for Projectile motion, circular motion is also an example of motion in a 2-D pla
    9 min read
    Projectile Motion
    Projectile motion refers to the curved path an object follows when it is thrown or projected into the air and moves under the influence of gravity. In this motion, the object experiences two independent motions: horizontal motion (along the x-axis) and vertical motion (along the y-axis). Projectile
    15+ min read
    Relative Motion
    Relative motion explains how the movement of an object is perceived differently depending on the observer’s frame of reference. For instance, while sitting on a moving train, a stationary train on the track appears to move backwards. This happens because the motion of the train you are in influences
    10 min read

    Rotational Mechanics

    Concepts of Rotational Motion
    Rotational motion refers to the movement of an object around a fixed axis. It is a complex concept that requires an understanding of several related concepts. Some of the important concepts related to rotational motion include angular displacement, angular velocity, angular acceleration, torque, the
    10 min read
    Angular Motion
    Angular Motion is the motion of an object around a fixed axis or point, or along a curved path with a constant angular velocity. It is also known as rotational motion. Another motion of an object is termed linear motion, which is a motion along a straight route. Linear motion variables are measured
    7 min read
    Angular Frequency
    Angular frequency is a fundamental concept in physics, particularly in studying wave motion and oscillations. It measures the angular displacement of a particle per unit time. In this article, we will learn about the meaning and definition of angular frequency, the formula of angular frequency, the
    10 min read
    Rotational Kinetic Energy
    Rotational Kinetic Energy is described as the kinetic energy associated with the rotation of an object around an axis. It is also known as angular kinetic energy. It is dependent on the mass of an object and its angular velocity. In this article, we will learn about rotational kinetic energy, its fo
    7 min read
    Torque
    Torque is the effect of force when it is applied to an object containing a pivot point or the axis of rotation (the point at which an object rotates), which results in the form of rotational motion of the object. The Force causes objects to accelerate in the linear direction in which the force is ap
    10 min read
    Angular Momentum
    Angular Momentum is a kinematic characteristic of a system with one or more point masses. Angular momentum is sometimes called Rotational Momentum or Moment of Momentum, which is the rotational equivalent of linear momentum. It is an important physical quantity as it is conserved for a closed system
    10 min read
    Centre of Mass
    Centre of Mass is the point of anybody where all the mass of the body is concentrated. For the sake of convenience in Newtonian Physics, we take the body as the point object where all its mass is concentrated at the centre of mass of the body. The centre of mass of the body is a point that can be on
    15 min read
    Centre of Gravity
    Centre of Gravity is one of the fundamental concepts in the study of gravitational force. Engineers and Scientists while dealing with mechanics and gravity often come across solid bodies which can't be represented by point masses such as celestial objects. In those cases, it is assumed as well as pr
    8 min read
    Radius of Gyration
    Radius of gyration, R, is a measure used in mechanics and engineering to describe the distribution of mass or inertia of an object relative to its axis of rotation. Radius of Gyration, or the radius of a body, is always centered on its rotational axis. It is a geometric characteristic of a rigid bod
    11 min read
    Moment of Inertia
    Moment of inertia is the property of a body in rotational motion. Moment of Inertia is the property of the rotational bodies which tends to oppose the change in rotational motion of the body. It is similar to the inertia of any body in translational motion. Mathematically, the Moment of Inertia is g
    15+ min read

    Fluid Mechanics

    Mechanical Properties of Fluids
    Fluids are substances that can flow and adapt to the shape of their container, including liquids and gases like water and air. Mechanical properties of fluids refer to viscosity, density, and pressure, which describe how fluids respond to external forces and influence their behavior in various situa
    11 min read
    What is Viscosity?
    Viscosity is the measurement of the resistance of the flowing liquid. Let us learn more about viscosity with an example suppose we take two bowls, one bowl contains water and the other has honey in it, we drop the content of both bowls then we see that water flows much faster than honey which conclu
    12 min read
    Buoyant Force
    Buoyancy is a phenomenon due to the buoyant force that causes an object to float. When you put an object in a liquid, an upward force is exerted on the object by the liquid. This force is equal to the weight of the liquid that has been displaced. The amount of liquid that has been displaced depends
    13 min read
    Archimedes Principle
    Archimedes Principle is a fundamental concept in fluid mechanics, credited to the ancient Greek mathematician and physicist Archimedes. According to Archimedes' Principle, when an object is immersed in a fluid the object experiences an upward force whose magnitude is equal to the weight of the fluid
    12 min read
    Pascal's Law
    Pascal's law establishes the relation between pressure and the height of static fluids. A static fluid is defined as a fluid that is not in motion. When the fluid is not flowing, it is said to be in hydrostatic equilibrium. For a fluid to be in hydrostatic equilibrium, the net force on the fluid mus
    10 min read
    Reynolds Number
    As liquid runs into a channel, it collides with the pipe. Engineers ensure that the liquid flow through the city's pipes is as consistent as possible. As a result, a number known as the Reynolds number predicts whether the flow of the liquid will be smooth or turbulent. Sir George Stoke was the firs
    6 min read
    Streamline Flow
    The substance that can change its form under an external force is defined as fluid. Whenever an external force is applied to a fluid, it begins to flow. The study of fluids in motion is defined as fluid dynamics. Have you ever noticed a creek flowing beneath the bridge? When you see a streamline, wh
    7 min read
    Laminar and Turbulent Flow
    Laminar flow and turbulent flow describe the movement patterns of fluids. Laminar flow is characterized by smooth, orderly layers of fluid sliding over one another without mixing, ideal for scenarios where minimal resistance is desired. Turbulent flow features chaotic, swirling patterns with irregul
    9 min read
    Bernoulli's Principle
    Bernoulli's Principle is a very important concept in Fluid Mechanics which is the study of fluids (like air and water) and their interaction with other fluids. Bernoulli's principle is also referred to as Bernoulli's Equation or Bernoulli Theorem. This principle was first stated by Daniel Bernoulli
    15+ min read
    Poiseuilles Law Formula
    According to Poiseuille's law, the flow of liquid varies depending on the length of the tube, the radius of the tube, the pressure gradient and the viscosity of the fluid. It is a physical law that calculates the pressure drop in an incompressible Newtonian fluid flowing in laminar flow through a lo
    4 min read
    Stoke's Law
    Stoke's Law: Observe a raindrop falling from a height if you look closely you will notice that the speed of all the raindrops is constant and even though it falls from a height under the influence of gravity its velocity seems constant. These questions are answered using Stoke's lawStoke's law was f
    11 min read

    Solid Mechanics

    What is Stress?
    Stress in physics is defined as the force exerted on the unit area of a substance. Stress affects the body as strain in which the shape of the body changes if the stress is applied and sometimes it gets permanently deformed. On the basis of the direction of force applied to the body, we can categori
    9 min read
    Stress and Strain
    Stress and Strain are the two terms in Physics that describe the forces causing the deformation of objects. Deformation is known as the change of the shape of an object by applications of force. The object experiences it due to external forces; for example, the forces might be like squeezing, squash
    12 min read
    Stress-Strain Curve
    Stress-Strain Curve is a very crucial concept in the study of material science and engineering. It describes the relationship between stress and the strain applied on an object. We know that stress is the applied force on the material, and strain, is the resulting change (deformation or elongation)
    11 min read
    Elasticity and Plasticity
    You've undoubtedly heard of the idea of elasticity by now. In layman's words, it indicates that after being stretched, some substances return to their former form. You've experimented with a slingshot. Didn't you? That is an elastic substance. Let us go into the ideas of elasticity and plasticity to
    9 min read
    Modulus of Elasticity
    Modulus of Elasticity or Elastic Modulus is the measurement of resistance offered by a material against the deformation force acting on it. Modulus of Elasticity is also called Young's Modulus. It is given as the ratio of Stress to Strain. The unit of elastic modulus is megapascal or gigapascal Modu
    12 min read
    Modulus of Rigidity
    Modulus of rigidity also known as shear modulus, is used to measure the rigidity of a given body. It is the ratio of shear stress to shear strain and is denoted by G or sometimes by S or μ. The modulus of rigidity of a material is directly proportional to its elastic modulus which depends on the mat
    11 min read
    Young's Modulus
    Young's Modulus is the ratio of stress and strain. It is named after the famous British physicist Thomas Young. Young's Modulus provides a relation between stress and strain in any object.  When a certain load is added to a rigid material, it deforms. When the weight is withdrawn from an elastic mat
    12 min read
    Bulk Modulus Formula
    For every material, the bulk modulus is defined as the proportion of volumetric stress to volumetric strain. The bulk modulus, in simpler terms, is a numerical constant that is used to quantify and explain the elastic characteristics of a solid or fluid when pressure is applied. We'll go over the bu
    4 min read
    Shear Modulus and Bulk Modulus
    A rigid body model is an idealised representation of an item that does not deform when subjected to external forces. It is extremely beneficial for evaluating mechanical systems—and many physical items are quite stiff. The degree to which an item may be regarded as stiff is determined by the physica
    7 min read
    Poisson's Ratio
    Poisson's Ratio is the negative ratio of transversal strain or lateral strain to the longitudinal strain of a material under stress. When a material particularly a rubber-like material undergoes stress the deformation is not limited to only one direction, rather it happens along both transversal and
    9 min read
    Stress, Strain and Elastic Potential Energy
    Elasticity, this term always reminds of objects like Rubber bands, etc. However, if the question arises, which one is more elastic- A rubber or an Iron piece? The answer will be an Iron piece. Why? The answer lies in the definition of Elasticity, elasticity is known to be the ability of the object t
    9 min read

    Thermodynamics

    Basics Concepts of Thermodynamics
    Thermodynamics is concerned with the ideas of heat and temperature, as well as the exchange of heat and other forms of energy. The branch of science that is known as thermodynamics is related to the study of various kinds of energy and its interconversion. The behaviour of these quantities is govern
    12 min read
    Zeroth Law of Thermodynamics
    Zeroth Law of Thermodynamics states that when two bodies are in thermal equilibrium with another third body than the two bodies are also in thermal equilibrium with each other. Ralph H. Fowler developed this law in the 1930s, many years after the first, second, and third laws of thermodynamics had a
    7 min read
    First Law of Thermodynamics
    First Law of Thermodynamics adaptation of the Law of Conservation of Energy differentiates between three types of energy transfer: Heat, Thermodynamic Work, and Energy associated with matter transfer. It also relates each type of energy transfer to a property of a body's Internal Energy. The First L
    8 min read
    Second Law of Thermodynamics
    Second Law of Thermodynamics defines that heat cannot move from a reservoir of lower temperature to a reservoir of higher temperature in a cyclic process. The second law of thermodynamics deals with transferring heat naturally from a hotter body to a colder body. Second Law of Thermodynamics is one
    10 min read
    Thermodynamic Cycles
    Thermodynamic cycles are used to explain how heat engines, which convert heat into work, operate. A thermodynamic cycle is used to accomplish this. The application determines the kind of cycle that is employed in the engine. The thermodynamic cycle consists of a series of interrelated thermodynamic
    15 min read
    Thermodynamic State Variables and Equation of State
    The branch of thermodynamics deals with the process of heat exchange by the gas or the temperature of the system of the gas. This branch also deals with the flow of heat from one part of the system to another part of the system. For systems that are present in the real world, there are some paramete
    5 min read
    Enthalpy: Definition, Formula and Reactions
    Enthalpy is the measurement of heat or energy in the thermodynamic system. It is the most fundamental concept in the branch of thermodynamics. It is denoted by the symbol H. In other words, we can say, Enthalpy is the total heat of the system. Let's know more about Enthalpy in detail below.Enthalpy
    12 min read
    State Functions
    State Functions are the functions that are independent of the path of the function i.e. they are concerned about the final state and not how the state is achieved. State Functions are most used in thermodynamics. In this article, we will learn the definition of state function, what are the state fun
    7 min read
    Carnot Engine
    A Carnot motor is a hypothetical motor that works on the Carnot cycle. Nicolas Leonard Sadi Carnot fostered the fundamental model for this motor in 1824. In this unmistakable article, you will find out about the Carnot cycle and Carnot Theorem exhaustively. The Carnot motor is a hypothetical thermod
    5 min read
    Heat Engine - Definition, Working, PV Diagram, Efficiency, Types
    Heat engines are devices that turn heat energy into motion or mechanical work. Heat engines are based on the principles of thermodynamics, specifically the conversion of heat into work according to the first and second laws of thermodynamics. They are found everywhere, from our cars, power plants to
    14 min read

    Wave and Oscillation

    Introduction to Waves - Definition, Types, Properties
    A wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities in physics, mathematics, and related subjects, commonly described by a wave equation. At least two field quantities in the wave medium are involved in physical waves. Periodic waves occur when variables o
    11 min read
    Wave Motion
    Wave Motion refers to the transfer of energy and momentum from one point to another in a medium without actually transporting matter between the two points. Wave motion is a kind of disturbance from place to place. Wave can travel in solid medium, liquid medium, gas medium, and in a vacuum. Sound wa
    12 min read
    Oscillation
    Oscillations are defined as the process of repeating vibrations of any quantity about its equilibrium position. The word “oscillation” originates from the Latin verb, which means to swing. An object oscillates whenever a force pushes or pulls it back toward its central point after displacement. This
    8 min read
    Oscillatory Motion Formula
    Oscillatory Motion is a form of motion in which an item travels over a spot repeatedly. The optimum situation can be attained in a total vacuum since there will be no air to halt the item in oscillatory motion friction. Let's look at a pendulum as shown below. The vibrating of strings and the moveme
    3 min read
    Amplitude Formula
    The largest deviation of a variable from its mean value is referred to as amplitude. It is the largest displacement from a particle's mean location in to and fro motion around a mean position. Periodic pressure variations, periodic current or voltage variations, periodic variations in electric or ma
    6 min read
    What is Frequency?
    Frequency is the rate at which the repetitive event that occurs over a specific period. Frequency shows the oscillations of waves, operation of electrical circuits and the recognition of sound. The frequency is the basic concept for different fields from physics and engineering to music and many mor
    9 min read
    Amplitude, Time Period and Frequency of a Vibration
    Sound is a form of energy generated by vibrating bodies. Its spread necessitates the use of a medium. As a result, sound cannot travel in a vacuum because there is no material to transfer sound waves. Sound vibration is the back and forth motion of an entity that causes the sound to be made. That is
    5 min read
    Energy of a Wave Formula
    Wave energy, often referred to as the energy carried by waves, encompasses both the kinetic energy of their motion and the potential energy stored within their amplitude or frequency. This energy is not only essential for natural processes like ocean currents and seismic waves but also holds signifi
    7 min read
    Simple Harmonic Motion
    Simple Harmonic Motion is a fundament concept in the study of motion, especially oscillatory motion; which helps us understand many physical phenomena around like how strings produce pleasing sounds in a musical instrument such as the sitar, guitar, violin, etc., and also, how vibrations in the memb
    15+ min read
    Displacement in Simple Harmonic Motion
    The Oscillatory Motion has a big part to play in the world of Physics. Oscillatory motions are said to be harmonic if the displacement of the oscillatory body can be expressed as a function of sine or cosine of an angle depending upon time. In Harmonic Oscillations, the limits of oscillations on eit
    10 min read

    Sound

    Production and Propagation of Sound
    Have you ever wonder how are we able to hear different sounds produced around us. How are these sounds produced? Or how a single instrument can produce a wide variety of sounds? Also, why do astronauts communicate in sign languages in outer space? A sound is a form of energy that helps in hearing to
    6 min read
    What are the Characteristics of Sound Waves?
    Sound is nothing but the vibrations (a form of energy) that propagates in the form of waves through a certain medium. Different types of medium affect the properties of the wave differently. Does this mean that Sound will not travel if the medium does not exist? Correct. It will not, It is impossibl
    7 min read
    Speed of Sound
    Speed of Sound as the name suggests is the speed of the sound in any medium. We know that sound is a form of energy that is caused due to the vibration of the particles and sound travels in the form of waves. A wave is a vibratory disturbance that transfers energy from one point to another point wit
    12 min read
    Reflection of Sound
    Reflection of Sound is the phenomenon of striking of sound with a barrier and bouncing back in the same medium. It is the most common phenomenon observed by us in our daily life. Let's take an example, suppose we are sitting in an empty hall and talking to a person we hear an echo sound which is cre
    9 min read
    Refraction of Sound
    A sound is a vibration that travels as a mechanical wave across a medium. It can spread via a solid, a liquid, or a gas as the medium. In solids, sound travels the quickest, comparatively more slowly in liquids, and the slowest in gases. A sound wave is a pattern of disturbance caused by energy trav
    5 min read
    How do we hear?
    Sound is produced from a vibrating object or the organ in the form of vibrations which is called propagation of sound and these vibrations have to be recognized by the brain to interpret the meaning which is possible only in the presence of a multi-functioning organ that is the ear which plays a hug
    7 min read
    Audible and Inaudible Sounds
    We hear sound whenever we talk, listen to some music, or play any musical instrument, etc. But did you ever wondered what is that sound and how is it produced? Or why do we hear to our own voice when we shout in a big empty room loudly? What are the ranges of sound that we can hear? In this article,
    10 min read
    Explain the Working and Application of SONAR
    Sound energy is the type of energy that allows our ears to sense something. When a body vibrates or moves in a ‘to-and-fro' motion, a sound is made. Sound needs a medium to flow through in order to propagate. This medium could be in the form of a gas, a liquid, or a solid. Sound propagates through a
    8 min read
    Noise Pollution
    Noise pollution is the pollution caused by sound which results in various problems for Humans. A sound is a form of energy that enables us to hear. We hear the sound from the frequency range of 20 to 20000 Hertz (20kHz). Humans have a fixed range for which comfortably hear a sound if we are exposed
    8 min read
    Doppler Effect - Definition, Formula, Examples
    Doppler Effect is an important phenomenon when it comes to waves. This phenomenon has applications in a lot of fields of science. From nature's physical process to planetary motion, this effect comes into play wherever there are waves and the objects are traveling with respect to the wave. In the re
    7 min read
    Doppler Shift Formula
    When it comes to sound propagation, the Doppler Shift is the shift in pitch of a source as it travels. The frequency seems to grow as the source approaches the listener and decreases as the origin fades away from the ear. When the source is going toward the listener, its velocity is positive; when i
    3 min read

    Electrostatics

    Electrostatics
    Electrostatics is the study of electric charges that are fixed. It includes an study of the forces that exist between charges as defined by Coulomb's Law. The following concepts are involved in electrostatics: Electric charge, electric field, and electrostatic force.Electrostatic forces are non cont
    13 min read
    Electric Charge
    Electric Charge is the basic property of a matter that causes the matter to experience a force when placed in a electromagnetic field. It is the amount of electric energy that is used for various purposes. Electric charges are categorized into two types, that are, Positive ChargeNegative ChargePosit
    8 min read
    Coulomb's Law
    Coulomb’s Law is defined as a mathematical concept that defines the electric force between charged objects. Columb's Law states that the force between any two charged particles is directly proportional to the product of the charge but is inversely proportional to the square of the distance between t
    9 min read
    Electric Dipole
    An electric dipole is defined as a pair of equal and opposite electric charges that are separated, by a small distance. An example of an electric dipole includes two atoms separated by small distances. The magnitude of the electric dipole is obtained by taking the product of either of the charge and
    11 min read
    Dipole Moment
    Two small charges (equal and opposite in nature) when placed at small distances behave as a system and are called as Electric Dipole. Now, electric dipole movement is defined as the product of either charge with the distance between them. Electric dipole movement is helpful in determining the symmet
    6 min read
    Electrostatic Potential
    Electrostatic potential refers to the amount of electrical potential energy present at a specific point in space due to the presence of electric charges. It represents how much work would be done to move a unit of positive charge from infinity to that point without causing any acceleration. The unit
    12 min read
    Electric Potential Energy
    Electrical potential energy is the cumulative effect of the position and configuration of a charged object and its neighboring charges. The electric potential energy of a charged object governs its motion in the local electric field.Sometimes electrical potential energy is confused with electric pot
    15+ min read
    Potential due to an Electric Dipole
    The potential due to an electric dipole at a point in space is the electric potential energy per unit charge that a test charge would experience at that point due to the dipole. An electric potential is the amount of work needed to move a unit of positive charge from a reference point to a specific
    7 min read
    Equipotential Surfaces
    When an external force acts to do work, moving a body from a point to another against a force like spring force or gravitational force, that work gets collected or stores as the potential energy of the body. When the external force is excluded, the body moves, gaining the kinetic energy and losing a
    9 min read
    Capacitor and Capacitance
    Capacitor and Capacitance are related to each other as capacitance is nothing but the ability to store the charge of the capacitor. Capacitors are essential components in electronic circuits that store electrical energy in the form of an electric charge. They are widely used in various applications,
    11 min read
geeksforgeeks-footer-logo
Corporate & Communications Address:
A-143, 7th Floor, Sovereign Corporate Tower, Sector- 136, Noida, Uttar Pradesh (201305)
Registered Address:
K 061, Tower K, Gulshan Vivante Apartment, Sector 137, Noida, Gautam Buddh Nagar, Uttar Pradesh, 201305
GFG App on Play Store GFG App on App Store
Advertise with us
  • Company
  • About Us
  • Legal
  • Privacy Policy
  • In Media
  • Contact Us
  • Advertise with us
  • GFG Corporate Solution
  • Placement Training Program
  • Languages
  • Python
  • Java
  • C++
  • PHP
  • GoLang
  • SQL
  • R Language
  • Android Tutorial
  • Tutorials Archive
  • DSA
  • Data Structures
  • Algorithms
  • DSA for Beginners
  • Basic DSA Problems
  • DSA Roadmap
  • Top 100 DSA Interview Problems
  • DSA Roadmap by Sandeep Jain
  • All Cheat Sheets
  • Data Science & ML
  • Data Science With Python
  • Data Science For Beginner
  • Machine Learning
  • ML Maths
  • Data Visualisation
  • Pandas
  • NumPy
  • NLP
  • Deep Learning
  • Web Technologies
  • HTML
  • CSS
  • JavaScript
  • TypeScript
  • ReactJS
  • NextJS
  • Bootstrap
  • Web Design
  • Python Tutorial
  • Python Programming Examples
  • Python Projects
  • Python Tkinter
  • Python Web Scraping
  • OpenCV Tutorial
  • Python Interview Question
  • Django
  • Computer Science
  • Operating Systems
  • Computer Network
  • Database Management System
  • Software Engineering
  • Digital Logic Design
  • Engineering Maths
  • Software Development
  • Software Testing
  • DevOps
  • Git
  • Linux
  • AWS
  • Docker
  • Kubernetes
  • Azure
  • GCP
  • DevOps Roadmap
  • System Design
  • High Level Design
  • Low Level Design
  • UML Diagrams
  • Interview Guide
  • Design Patterns
  • OOAD
  • System Design Bootcamp
  • Interview Questions
  • Inteview Preparation
  • Competitive Programming
  • Top DS or Algo for CP
  • Company-Wise Recruitment Process
  • Company-Wise Preparation
  • Aptitude Preparation
  • Puzzles
  • School Subjects
  • Mathematics
  • Physics
  • Chemistry
  • Biology
  • Social Science
  • English Grammar
  • Commerce
  • World GK
  • GeeksforGeeks Videos
  • DSA
  • Python
  • Java
  • C++
  • Web Development
  • Data Science
  • CS Subjects
@GeeksforGeeks, Sanchhaya Education Private Limited, All rights reserved
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox
Improvement
Suggest Changes
Help us improve. Share your suggestions to enhance the article. Contribute your expertise and make a difference in the GeeksforGeeks portal.
geeksforgeeks-suggest-icon
Create Improvement
Enhance the article with your expertise. Contribute to the GeeksforGeeks community and help create better learning resources for all.
geeksforgeeks-improvement-icon
Suggest Changes
min 4 words, max Words Limit:1000

Thank You!

Your suggestions are valuable to us.

What kind of Experience do you want to share?

Interview Experiences
Admission Experiences
Career Journeys
Work Experiences
Campus Experiences
Competitive Exam Experiences