Bernoulli's Principle, formulated by Daniel Bernoulli and later expressed as Bernoulli's Equation by Leonhard Euler in 1752, is a fundamental concept in fluid mechanics. It describes the relationship between the pressure (P), velocity, and height (h) of a fluid in motion. The principle states that in a steady, incompressible flow, an increase in the fluid's velocity results in a decrease in its pressure or potential energy.
What is Bernoulli’s Principle?
Bernoulli's Principle states that in a flowing fluid, where the speed is higher, the pressure is lower, and where the speed is lower, the pressure is higher, assuming the fluid is flowing horizontally. This principle explains how the gravitational potential energy, pressure energy, and kinetic energy of the fluid combine to form the total mechanical energy of the flow, which remains constant.
In real life, Bernoulli’s Principle can be observed in rivers. In areas where the river's width increases, the speed of the water decreases. Conversely, in narrower sections of the river, the speed of the water increases, as the fluid is forced to flow faster through the constricted area.
Bernoulli's Principle is formulated into an equation called Bernoulli's Equation. Bernoulli's Equation is a relationship between kinetic energy, gravitational potential energy, and the pressure of the fluid inside the container.
Thus, Bernoulli’s Principle Formula is stated as:
ρ+1/2ρv2+ ρgh = constant
where,
- P is the Pressure exerted by the fluid,
- ρ is the Density of the fluid,
- v is the Velocity of the fluid,
- g is the Acceleration due to gravity and
- h is the Height of the container.
Derivation of Bernoulli’s Equation
Consider a container in the form of a pipe, with two openings positioned at different heights and having varying diameters. The relationship between the cross-sectional areas A, flow speed v, height from the ground y, and pressure P at two distinct points, 1 and 2, is illustrated in the diagram below.

As illustrated in the diagram, the pipe should be at various heights. According to the equation of continuity, its velocity must fluctuate. To achieve this acceleration and force are required, which is produced by the fluid surrounding it, and the pressure in different places must be different.
Before, deriving Bernoulli’s Equation, we assume that the fluid has no viscous forces, so the fluid's energy will be conserved. Also, the density of the fluid flowing at both points of the container must be uniform.
To determine Bernoulli's equation, we must first determine how much work done experienced by the fluid,
The work done at point 1 where the force F1 is exerted to displace the fluid to dx1 is
dW1 = F1 dx1
Here, the force exerted at point 1 is given by, F1 = P1A1
where P1 and A1 are the pressure exerted and cross-sectional area at point 1.
This implies,
dW1 = P1A1 dx1
⇒ dW1 = P1 dv
Similarly, the work done by the fluid at point 2 is:
dW2 = P2A2 dx2
⇒ dW2 = P2 dv
Now, the total work done by the fluid flowing through the container is,
dW = P1 dv - P2 dv
⇒ dW = (P1 - P2) dv . . .(1)
Now, the change in the kinetic energy of the fluid is given by,
\begin{aligned}\text{d}K&=\dfrac{1}{2}m_2v^2_2-\dfrac{1}{2}m_1v^2_1\end{aligned}
But, the mass m of the fluid can be written as,
m = ρ dv
Therefore,
\begin{aligned}\text{d}K=\dfrac{1}{2}\rho dv (v^2_2-v^2_1)\end{aligned} . . . (2)
Similarly, the change in gravitational potential energy is given by,
\begin{aligned}\text{d}U&=\dfrac{1}{2}m_1gy_2-\dfrac{1}{2}m_2gy_1\\\Rightarrow \text{d}U&=\dfrac{1}{2}\rho dv g(y_2-y_1)\end{aligned} . . . (3)
According to the law of conservation of energy:
dW = dK + dU
\begin{aligned}&(P_1 - P_2) dv=\dfrac{1}{2}\rho dv (v^2_2-v^2_1)+\dfrac{1}{2}\rho dv g(y_2-y_1)\\ \Rightarrow & (P_1-P_2)=\dfrac{1}{2}\rho (v^2_2-v^2_1)+\dfrac{1}{2}\rho g(y_2-y_1)\\ &\Rightarrow P_1+\dfrac{1}{2}\rho v_1^2+\rho gy_1=P_2+\dfrac{1}{2}\rho v_2^2+\rho gy_2\end{aligned}
This is Bernoulli’s equation and this can be written as a general expression,
\bold{P+\frac{1}{2}\rho v^2+\rho gh=\text{Constant} }
Bernoulli’s Equation at Constant Depth
As the name suggests, let us suppose any fluid is moving at some constant depth, so h1 = h2, under this condition Bernoulli's equation be
P_1+\frac{1}{2}\rho v_1^2+\rho gh_1 = P_2+\frac{1}{2}\rho v_2^2+\rho gh_2
\Rightarrow P_1+\frac{1}{2}\rho v_1^2= P_2+\frac{1}{2}\rho v_2^2 (As h1 = h2 ⇒ ρgh1 = ρgh2)
Bernoulli’s Equation for Static Fluids
Any fluid is said static if there is no motion in it, for example, oil in a container, a calm lake, the air in a room with no air current, etc. For static fluid there is no velocity gradient throughout the fluid, thus v1 = v2. So, under this condition Bernoulli's equation be.
P_1+\frac{1}{2}\rho v_1^2+\rho gh_1 = P_2+\frac{1}{2}\rho v_2^2+\rho gh_2
\Rightarrow P_1+\rho gh_1 = P_2+\rho gh_2
Now, to simplify it much further, h2 = 0 (any height can be chosen for the reference height to be zero)
\Rightarrow P_2 = P_1+\rho gh_1 ,
This equation tells us that the static pressure increase from point 1 to 2 by ρgh1.
Principle of Continuity
The primary consideration when representing the flow of fluids or gases is the continuity equation, which reflects the conservation of mass. It demonstrates how mass is conserved as fluids or gases flow through a system, meaning the mass entering a given point must equal the mass exiting that point, assuming no accumulation within the system."
"The principle of continuity states that for an incompressible fluid in streamline flow, the mass flow rate is constant across any cross-sectional area. This means the product of velocity and cross-sectional area remains the same along the flow."
"The flow and behavior of fluids in a pipe are described by the continuity equation. This principle explains the flow of liquids and gases through pipes, ducts, rivers, and other conduits."
Consider a pipe as shown above, with different cross-sectional areas A1 and A2. Let the rate of mass entering and leaving the given system be M1 and M2 respectively, with a speed of flow v, and density ρ of the fluid.

Then, according to the principle of continuity, the rate of mass of fluid entering must be equal to the rate of mass of fluid leaving the system.
Since, the rate of mass entering, M1 = ρA1V1 Δt and
The rate of mass entering, M2 = ρA2V2 Δt
Therefore,
ρA1V1 Δt = ρA2V2 Δt
ρA1V1= ρA2V2
The above equation is now termed as Equation of Continuity.
Applications of Bernoulli's Theorem and Equation
Here are some key applications of Bernoulli's Principle:
Venturi Meter
A Venturi meter is a device used to measure the flow rate of a fluid in a pipe with varying cross-sectional areas. It works based on the principle that the fluid's velocity increases and pressure decreases as it passes through a narrower section of the pipe.
To the wide and narrow sections of the pipe, we apply Bernoulli's equation, where h1=h2. The pressure P2 is less than P1 because A1 is bigger than A2, and v2 is greater than v1. The fluid is accelerated as it enters the tube, which is narrow, and slowed as it exits by a net force to the left.

The venturi meter formula is stated as,
\bold{v_1=\sqrt{\dfrac{2gh}{\left(\dfrac{A_1}{A_2}\right)^2-1}}}
where,
- v1 is the rate of fluid flowing,
- g is the acceleration due to gravity,
- h is the difference in liquid level in the two tubes,
- A1 and A2 are the cross-sectional areas of the tube.
Principle of Lifting an Aircraft
Bernoulli's theorem plays a key role in the operation of airplanes. The wings of an aircraft are designed with a specific shape to take advantage of this principle. As the plane moves, air flows over and under the wings at different speeds. According to Bernoulli's principle, the faster-moving air above the wing creates lower pressure compared to the slower air below the wing.
This pressure difference generates an upward force on the wings. When this upward force exceeds the plane's weight, it causes the aircraft to lift, as shown in the diagram below.

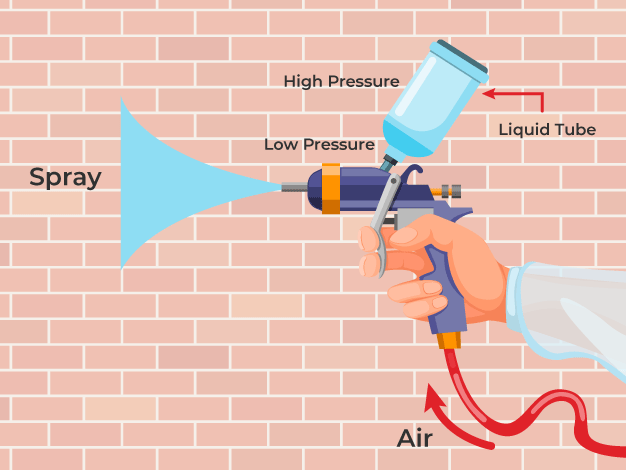
Action of Atomizer or Spray Gun
When the piston is pulled, air flows out of the horizontal tube, causing the pressure to drop which is less than the container's pressure. The consequence is that the liquid in the vertical tube rises. When it runs into the fast air in the tube, it dissipates into a thin mist. The same idea governs filter pumps, Bunsen burners, and sprayers used to apply pesticides or scents.
Conservation of Energy and Bernoulli’s Equation
Bernoulli’s theorem states that in a steady-flowing, incompressible fluid, the sum of kinetic energy, potential energy, and pressure energy remains constant along a streamline. However, several conditions must be met for the equation to hold:
- Steady Flow: The fluid’s velocity, pressure, and density should not change over time. If the flow is unsteady, the equation may not apply.
- Incompressibility: The fluid must be incompressible (typically true for liquids), though for gases, density must remain constant, with minimal variations in pressure, velocity, and temperature.
- Irrotational Flow: The fluid must flow in such a way that there is no rotational motion or angular momentum, ensuring the flow is irrotational.
- Ideal Fluid: The principle assumes no energy loss due to friction. Therefore, the fluid must be ideal, with no internal viscosity or frictional forces that would cause energy dissipation.
Solved Examples on Bernoulli's Principle
Example 1: Water is flowing at a rate of 2m/s through a tube with a diameter of 1 m. If the pressure at this point is 80 kPa, what is the pressure of the water after the tube narrows to a diameter of 0.5m? ρwater=1.0 kgl-1
Solution:
According to Bernoulli’s expression:
P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}
The height is same (h1=h2), so the expression can be written as
P_{2}=P_{1}+\frac{1}{2}\rho \left(v^2_{1}-v^2_{2}\right)
The expression for the cross-sectional area is
A_{1}=\pi\frac{ d^2}{4}\\ \Rightarrow A_{1}=\pi\frac{ 1^2}{4}\text{ m}^2\\ \Rightarrow A_{1}=\frac{\pi}{4}\text{ m}^2\\
Similarly
A_{2}=\pi\frac{ d^2}{4}\\ \Rightarrow A_{2}=\pi\frac{ 0.5^2}{4}\text{ m}^2\\ \Rightarrow A_{2}=\frac{\pi}{16}\text{ m}^2\\
The expression for the velocity for each diameter is
v_1=\frac{V}{A}\\ \Rightarrow v_1=\frac{2}{\frac{\pi}{4}}\frac{\text{m}}{s}\\ \Rightarrow v_1=\frac{8}{\pi}\frac{\text{m}}{s}
Similarly,
v_2=\frac{2}{\frac{\pi}{16}}\frac{\text{m}}{s}\\ \Rightarrow v_2=\frac{32}{\pi}\frac{\text{m}}{s}
Substitute the value in Bernoulli’s expression:
P_{2}=80000\text{ Pa}+\frac{1}{2}\times1000\frac{\text{kg}}{\text{m}^3}\times\left(\frac{8}{\pi}-\frac{32}{\pi}\right)\frac{\text{m}}{s}\\ \Rightarrow P_{2}=76.2\text{ kPa}
Example 2: Explain why:
(a) The blood pressure in humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at sea level, though the height of the atmosphere is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though the pressure is force divided by area.
Solution:
(a) The height of the blood column in the foot is greater than that in the brain. As a result, human blood pressure is higher in the feet than in the brain.
(b) The relationship between air density and height is not linear. As a result, pressure does not decrease linearly with height. P = P0e–αh gives the air pressure at a height h, where P0 is the pressure of air at sea level and α is a constant.
(c) When a force is applied to a liquid, the pressure is distributed evenly throughout the liquid. As a result, the pressure due to liquid has no definite direction. As a result, hydrostatic pressure is a scalar value.
Example 3: Drive the expression for Bernoulli’s principle.
Solution:
The flow of an ideal fluid in a pipe of varying cross-section. The fluid in a section of length v1∆t moves to the section of length v2∆t in time ∆t
Consider the flow at two regions BC and DE. Take a look at the flow in two different regions: BC and DE. Consider the fluid that present between B and D would travelled in an infinitesimal time interval ∆t. If v1 is the speed at B and v2 is the speed at D, the fluid at B has travelled a distance of v1∆t to C i.e.
dx_{1}=v_{1}\Delta{t}
In the same interval ∆t the fluid initially at D moves to E, a distance equal to v2∆t i.e.
dx_{2}=v_{2}\Delta{t}
The areas A1 and A2 has the pressures P1 and P2. The work done on the fluid at BC is
W_{1}=P_{1}A_{1}\cdot v_{1}\Delta{t}\\ \Rightarrow W_{1}=P_{1}\Delta{V}
where ∆V is the volume passes through region BC.
Since the same volume ∆V passes through both the regions BC and DE. therefore the expression for the work done by the fluid at the another end DE is
W_{2}=P_{2}A_{2}\cdot v_{2}\Delta{t}\\ \Rightarrow W_{2}=P_{2}\Delta{V}
So the total work done on the fluid is
W_{1}-W_{2}=P_{1}\Delta{V}-P_{2}\Delta{V}\\ \Rightarrow W_{1}-W_{2}=\left(P_{1}-P_{2}\right)\Delta{V}
Let the density of the fluid is ρ therefore the expression ∆m = ρ∆V is the mass passing through the pipe in time ∆t, then change in gravitational potential energy is
\Delta{U} =\rho g\Delta{V}\left(h_{2}-h_{1}\right)
The change in its kinetic energy is given by
\Delta{K}=\frac{1}{2}\rho\Delta{V}\left(v^2_{2}-v^2_{1}\right)
According to he work – energy theorem'
\left(P_{1}-P_{2}\right)\Delta{V}=\frac{1}{2}\rho \Delta{V}\left(v^2_{2}-v^2_{1}\right)+\rho g\Delta{V}\left(h_{2}-h_{1}\right)\\ \Rightarrow \left(P_{1}-P_{2}\right)=\frac{1}{2}\rho\left(v^2_{2}-v^2_{1}\right)+\rho g\left(h_{2}-h_{1}\right)
Rearrange the above expression,
P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}
This is Bernoulli’s equation and this can written as general expression.
P + 1/2ρv2 + ρgh = constant
Example 4: Suppose that a huge tank 50m high and filled with water is open to the atmosphere and is hit by a bullet that pierces one side of the tank, allowing water to flow out. The hole is 2m above the ground. If the hole is very small in comparison with the size of the tank, how quickly will the water flow out of the tank?
Solution:
According to Bernoulli’s expression:
P_{1}+\frac{1}{2}\rho v^2_{1}+\rho gh_{1}=P_{2}+\frac{1}{2}\rho v^2_{2}+\rho gh_{2}
According to question it is assumed that the top of the container as point 1, and the hole where water is flowing out as point 2. Both points are open to the atmosphere. Therefore, the pressure on each side of the above equation is equal to 1 atm, and thus it got cancel. The size of the hole on the side of the tank is so small compared to the rest of the tank, the velocity of the water at point 1 is nearly equal to 0. Hence, we can cancel out the 1/2ρ(v1)2 term on the left side of the equation. The expression can rewrite as,
\rho gh_1=\frac{1}{2}\rho v^2_{2}+\rho gh_{2}\\ \Rightarrow gh_1=\frac{1}{2}v^2_{2}+gh_{2}\\ \Rightarrow v^2_{2}=2\left(gh_1-gh_2\right)\\ \Rightarrow v_{2}=\sqrt{2g\left(h_1-h_2\right)}\\
Substitute the values in the above expression,
v2 = √{2×(9.8)×(50-2)}
v2 = 30.67 ms-1
Practice Problems on Bernoulli's Theorem
Problem 1: A fluid is flowing steadily through a pipe. At one point in the pipe, the fluid has a velocity of 10 m/s and a pressure of 200,000 Pa. If the pipe narrows downstream, and the velocity of the fluid increases to 15 m/s, what is the pressure at that point?
Problem 2: An airplane is flying at a constant altitude. The air pressure on the upper surface of the wing is 90,000 Pa, while the air pressure on the lower surface of the wing is 100,000 Pa. If the speed of the air over the top of the wing is 250 m/s, what is the speed of the air under the wing?
Problem 3: Water is flowing through a hose with a diameter of 2 cm at a speed of 4 m/s. If the hose narrows to a diameter of 1 cm, what is the speed of the water at that point? Assume incompressible flow.
Problem 4: A hydraulic lift is used to lift a car weighing 12,000 N. The piston on which the car sits has an area of 0.2 square meters. If a smaller piston connected to the same hydraulic system has an area of 0.02 square meters, how much force must be applied to the smaller piston to lift the car?
Conclusion
Bernoulli's principle in fluid dynamics states that as the speed of a fluid increases, its pressure decreases, or its potential energy reduces. In other words, faster-moving fluids exert lower pressure than slower-moving ones. This principle arises from the conservation of energy in flowing fluids.
You may also Read,
Similar Reads
Physics Tutorial The term "physics" is derived from the Greek word physis (meaning “natureâ€) and physika (meaning “natural thingsâ€). It is the study of matter, energy, and the fundamental forces of nature, seeking to understand the behaviour of the universe from the smallest subatomic particles to the largest galaxi
15+ min read
Mechanics
Rest and MotionRest and motion describe the state of objects in relation to their surroundings. Whether an object is at rest or in motion, these states can be analyzed and understood through the principles of physics. When an object changes its position with respect to a stationary object with the passage of time,
10 min read
ForceForce is defined as an external cause that a body experiences as a result of interacting with another body. Whenever two objects interact, a force is exerted on each object. In general-term "To Push or Pull an Object" is defined as the force. The force is the interaction experience by the object be
11 min read
What is Pressure?Have you ever thought about why a needle is so thin, why fence spikes are pointed, or why a hammer's head is flat? It’s all about pressure. Pressure is the force applied to a specific area. A needle’s sharp tip concentrates the force, allowing it to easily pierce fabric. If it were blunt, the force
7 min read
FrictionFriction in Physics is defined as a type of force that always opposes the motion of the object on which it is applied. Suppose we kick a football and it rolls for some distance and eventually it stops after rolling for some time. This is because of the friction force between the ball and the ground.
8 min read
Inertia MeaningInertia is the basic concept of physics that is explained using the concept of Mass. The inertial concept was first explained by Sir Isaac Newton and the Law of Inertia is explained as any object in a state of rest or in a state of motion always staying in its state of rest or motion until an extern
8 min read
Newton's Laws of Motion | Formula, Examples and QuestionsNewton's Laws of Motion, formulated by the renowned English physicist Sir Isaac Newton, are fundamental principles that form the core of classical mechanics. These three laws explain how objects move and interact with forces, shaping our view of everything from everyday movement to the dynamics of c
9 min read
Universal Law of GravitationUniversal Law of Gravitation or Newton's law of Universal Gravitation as the name suggests is given by Sir Isaac Newton. This law helps us to understand the motion of very large bodies in the universe. According to this law, an attractive force always acts between two bodies that have masses. The st
15 min read
What is Gravity?There is a story about the discovery of gravity which says that Newton discovered gravity in the year 1665 when he was sitting under the apple tree, and suddenly an apple fell on his head, which led him to the question about falling objects. He questioned himself why all objects fall and also questi
12 min read
Law of Conservation of EnergyLaw of Conservation of Energy is the most fundamental law of physics which states that "Energy can neither be created nor be destroyed it can only change from one form of the energy to another form of the energy." It is the fundamental law of Physics that governs various processes in our environment
11 min read
Free Body DiagramFree Body Diagram often called FBD is a way of representing all the forces acting on a body at a particular instant in a simpler form. It enables the calculation of the net force acting on the body and its direction of motion by making a symbolic diagram of all the forces acting on a body. In this a
10 min read
Inclined PlaneInclined Plane is the most fundamental forms of mechanical devices used in physics. In order to get around physical obstacles and simplify tasks, inclined planes have been used for centuries in both ancient and recent construction projects. A flat surface that is angled with respect to the horizonta
10 min read
Work DoneEvery day, we are involved in countless activities—from lifting a school bag, climbing stairs, or opening a door to pushing a swing in the park. While these tasks may seem different, they all have something in common: they require effort. But what exactly makes something happen when we apply effort?
12 min read
Conservative Forces - Definition, Formula, ExamplesConservative Force is a type of force which is independent of path taken to do a work. This means when an when force applied in moving an object from one position to another is the same irrespective of the path taken, it is called conservative force. A force is a push or pull acting on an object. In
7 min read
EnergyEnergy is a word we hear frequently—whether it's about feeling energetic, saving energy, or generating power. However, in physics, energy carries a very precise meaning. It is defined as the capacity to perform work or bring about change. Everything around us involves energy in one form or another.
10 min read
Frame of ReferenceFrame of reference is a way to observe and measure objects' positions and movements. It acts like a coordinate system, helping us understand where things are and how they move. By using a frame of reference, we can describe motion accurately. It makes it clear if something is moving fast, slow, or a
6 min read
Kinematics
Kinematics | Definition, Formula, Derivation, ProblemsKinematics is the study of motion of points, objects, and systems by examining their motion from a geometric perspective, without focusing on the forces that cause such movements or the physical characteristics of the objects involved. This study area uses algebra to create mathematical models that
10 min read
What is Motion?Motion is the change in position over time, and it’s always measured with reference to a specific point, called the origin. To describe this change, we use two key terms: distance and displacement. Distance is the total path covered during motion and only has magnitude, while displacement is the sho
9 min read
Distance and DisplacementDistance and Displacement are two important terms of mechanics that may seem the same but have different meanings and definitions. Distance is a measure of "How much path is covered by an object in motion?" While Displacement is the measure of "How much path is covered by the object in a particular
5 min read
Speed and VelocityMechanics can be termed as the branch of physics concerned with the concepts of energy and forces and their effect on bodies. It governs the relationships related to the motion of objects, that is, between matter, force, and its associated energy. It is responsible for the motion of bodies and the a
13 min read
AccelerationAcceleration is defined as the rate of change in velocity. This implies that if an object’s velocity is increasing or decreasing, then the object is accelerating. Acceleration has both magnitude and direction, therefore it is a Vector quantity. According to Newton's Second Law of Motion, acceleratio
9 min read
What is Momentum Equation?What is Momentum in Physics?The concept of Momentum in physics is very important, without which most of the theories in physics will fail. The momentum can be calculated by multiplying the mass of the substance and its velocity. In physics, momentum is of different types and forms. Let's know more a
6 min read
Equations of Motion: Derivations and ExamplesEquations of Motion was given by Sir Issac Newton; who is considered the father of mechanics. He was the first to give the fundamental physical laws that deal with objects and their motion. He formulated three equations of motion of an object and published them in his book Philosophiae Naturalis Pri
11 min read
Uniform Circular MotionUniform Circular Motion as the name suggests, is the motion of a moving object with constant speed in a circular path. As we know, motion in a plane only has two coordinates, either x, and y, y and z, or z and x. Except for Projectile motion, circular motion is also an example of motion in a 2-D pla
9 min read
Projectile MotionProjectile motion refers to the curved path an object follows when it is thrown or projected into the air and moves under the influence of gravity. In this motion, the object experiences two independent motions: horizontal motion (along the x-axis) and vertical motion (along the y-axis). Projectile
15+ min read
Relative MotionRelative motion explains how the movement of an object is perceived differently depending on the observer’s frame of reference. For instance, while sitting on a moving train, a stationary train on the track appears to move backwards. This happens because the motion of the train you are in influences
10 min read
Rotational Mechanics
Concepts of Rotational MotionRotational motion refers to the movement of an object around a fixed axis. It is a complex concept that requires an understanding of several related concepts. Some of the important concepts related to rotational motion include angular displacement, angular velocity, angular acceleration, torque, the
10 min read
Angular MotionAngular Motion is the motion of an object around a fixed axis or point, or along a curved path with a constant angular velocity. It is also known as rotational motion. Another motion of an object is termed linear motion, which is a motion along a straight route. Linear motion variables are measured
7 min read
Angular FrequencyAngular frequency is a fundamental concept in physics, particularly in studying wave motion and oscillations. It measures the angular displacement of a particle per unit time. In this article, we will learn about the meaning and definition of angular frequency, the formula of angular frequency, the
10 min read
Rotational Kinetic EnergyRotational Kinetic Energy is described as the kinetic energy associated with the rotation of an object around an axis. It is also known as angular kinetic energy. It is dependent on the mass of an object and its angular velocity. In this article, we will learn about rotational kinetic energy, its fo
7 min read
TorqueTorque is the effect of force when it is applied to an object containing a pivot point or the axis of rotation (the point at which an object rotates), which results in the form of rotational motion of the object. The Force causes objects to accelerate in the linear direction in which the force is ap
10 min read
Angular MomentumAngular Momentum is a kinematic characteristic of a system with one or more point masses. Angular momentum is sometimes called Rotational Momentum or Moment of Momentum, which is the rotational equivalent of linear momentum. It is an important physical quantity as it is conserved for a closed system
10 min read
Centre of MassCentre of Mass is the point of anybody where all the mass of the body is concentrated. For the sake of convenience in Newtonian Physics, we take the body as the point object where all its mass is concentrated at the centre of mass of the body. The centre of mass of the body is a point that can be on
15 min read
Centre of GravityCentre of Gravity is one of the fundamental concepts in the study of gravitational force. Engineers and Scientists while dealing with mechanics and gravity often come across solid bodies which can't be represented by point masses such as celestial objects. In those cases, it is assumed as well as pr
8 min read
Radius of GyrationRadius of gyration, R, is a measure used in mechanics and engineering to describe the distribution of mass or inertia of an object relative to its axis of rotation. Radius of Gyration, or the radius of a body, is always centered on its rotational axis. It is a geometric characteristic of a rigid bod
11 min read
Moment of InertiaMoment of Inertia is a property of a body in rotational motion that resists changes in its rotational state. It is analogous to mass (inertia) in linear motion. Mathematically, it is defined as the sum of the product of each particle’s mass and the square of its distance from the axis of rotation: I
15+ min read
Fluid Mechanics
Mechanical Properties of FluidsFluids are substances that can flow and adapt to the shape of their container, including liquids and gases like water and air. Mechanical properties of fluids refer to viscosity, density, and pressure, which describe how fluids respond to external forces and influence their behavior in various situa
11 min read
What is Viscosity?Viscosity is a fundamental property of liquids that describes their internal resistance to flow. Imagine three bowls—one filled with water and the other with oil and honey. If you were to tip the three bowls and observe the flow, you’d quickly notice that water pours out much faster than oil and hon
10 min read
Buoyant ForceBuoyancy is a phenomenon due to the buoyant force that causes an object to float. When you put an object in a liquid, an upward force is exerted on the object by the liquid. This force is equal to the weight of the liquid that has been displaced. The amount of liquid that has been displaced depends
13 min read
Archimedes PrincipleArchimedes Principle is a fundamental concept in fluid mechanics, credited to the ancient Greek mathematician and physicist Archimedes. According to Archimedes' Principle, when an object is immersed in a fluid the object experiences an upward force whose magnitude is equal to the weight of the fluid
12 min read
Pascal's LawPascal's law establishes the relation between pressure and the height of static fluids. A static fluid is defined as a fluid that is not in motion. When the fluid is not flowing, it is said to be in hydrostatic equilibrium. For a fluid to be in hydrostatic equilibrium, the net force on the fluid mus
10 min read
Reynolds NumberAs liquid runs into a channel, it collides with the pipe. Engineers ensure that the liquid flow through the city's pipes is as consistent as possible. As a result, a number known as the Reynolds number predicts whether the flow of the liquid will be smooth or turbulent. Sir George Stoke was the firs
6 min read
Streamline FlowThe substance that can change its form under an external force is defined as fluid. Whenever an external force is applied to a fluid, it begins to flow. The study of fluids in motion is defined as fluid dynamics. Have you ever noticed a creek flowing beneath the bridge? When you see a streamline, wh
7 min read
Laminar and Turbulent FlowLaminar flow and turbulent flow describe the movement patterns of fluids. Laminar flow is characterized by smooth, orderly layers of fluid sliding over one another without mixing, ideal for scenarios where minimal resistance is desired. Turbulent flow features chaotic, swirling patterns with irregul
9 min read
Bernoulli's PrincipleBernoulli's Principle, formulated by Daniel Bernoulli and later expressed as Bernoulli's Equation by Leonhard Euler in 1752, is a fundamental concept in fluid mechanics. It describes the relationship between the pressure (P), velocity, and height (h) of a fluid in motion. The principle states that i
14 min read
Poiseuilles Law FormulaAccording to Poiseuille's law, the flow of liquid varies depending on the length of the tube, the radius of the tube, the pressure gradient and the viscosity of the fluid. It is a physical law that calculates the pressure drop in an incompressible Newtonian fluid flowing in laminar flow through a lo
4 min read
Stoke's LawStoke's Law: Observe a raindrop falling from a height if you look closely you will notice that the speed of all the raindrops is constant and even though it falls from a height under the influence of gravity its velocity seems constant. These questions are answered using Stoke's lawStoke's law was f
11 min read
Solid Mechanics
What is Stress?Stress in physics is defined as the force exerted on the unit area of a substance. Stress affects the body as strain in which the shape of the body changes if the stress is applied and sometimes it gets permanently deformed. On the basis of the direction of force applied to the body, we can categori
9 min read
Stress and StrainStress and Strain are the two terms in Physics that describe the forces causing the deformation of objects. Deformation is known as the change of the shape of an object by applications of force. The object experiences it due to external forces; for example, the forces might be like squeezing, squash
12 min read
Stress-Strain CurveStress-Strain Curve is a very crucial concept in the study of material science and engineering. It describes the relationship between stress and the strain applied on an object. We know that stress is the applied force on the material, and strain, is the resulting change (deformation or elongation)
11 min read
Elasticity and PlasticityYou've undoubtedly heard of the idea of elasticity by now. In layman's words, it indicates that after being stretched, some substances return to their former form. You've experimented with a slingshot. Didn't you? That is an elastic substance. Let us go into the ideas of elasticity and plasticity to
9 min read
Modulus of ElasticityModulus of Elasticity or Elastic Modulus is the measurement of resistance offered by a material against the deformation force acting on it. Modulus of Elasticity is also called Young's Modulus. It is given as the ratio of Stress to Strain. The unit of elastic modulus is megapascal or gigapascal Modu
12 min read
Modulus of RigidityModulus of rigidity also known as shear modulus, is used to measure the rigidity of a given body. It is the ratio of shear stress to shear strain and is denoted by G or sometimes by S or μ. The modulus of rigidity of a material is directly proportional to its elastic modulus which depends on the mat
11 min read
Young's ModulusYoung's Modulus is the ratio of stress and strain. It is named after the famous British physicist Thomas Young. It is also known as the "Modulus of Elasticity" and is a fundamental property that describes the relationship between stress and strain in elastic materials. It explains how a material def
8 min read
Bulk Modulus FormulaThe modulus of elasticity measures a material's resistance to elastic deformation under external forces. Understanding this property is important for designing structures with materials like metals, concrete, and polymers to ensure they can withstand stresses without permanent deformation.The modulu
7 min read
Shear Modulus and Bulk ModulusA rigid body model is an idealised representation of an item that does not deform when subjected to external forces. It is extremely beneficial for evaluating mechanical systems—and many physical items are quite stiff. The degree to which an item may be regarded as stiff is determined by the physica
7 min read
Poisson's RatioPoisson's Ratio is the negative ratio of transversal strain or lateral strain to the longitudinal strain of a material under stress. When a material particularly a rubber-like material undergoes stress the deformation is not limited to only one direction, rather it happens along both transversal and
9 min read
Stress, Strain and Elastic Potential EnergyElasticity, this term always reminds of objects like Rubber bands, etc. However, if the question arises, which one is more elastic- A rubber or an Iron piece? The answer will be an Iron piece. Why? The answer lies in the definition of Elasticity, elasticity is known to be the ability of the object t
9 min read
Thermodynamics
Basics Concepts of ThermodynamicsThermodynamics is concerned with the ideas of heat and temperature, as well as the exchange of heat and other forms of energy. The branch of science that is known as thermodynamics is related to the study of various kinds of energy and its interconversion. The behaviour of these quantities is govern
12 min read
Zeroth Law of ThermodynamicsZeroth Law of Thermodynamics states that when two bodies are in thermal equilibrium with another third body than the two bodies are also in thermal equilibrium with each other. Ralph H. Fowler developed this law in the 1930s, many years after the first, second, and third laws of thermodynamics had a
7 min read
First Law of ThermodynamicsFirst Law of Thermodynamics adaptation of the Law of Conservation of Energy differentiates between three types of energy transfer: Heat, Thermodynamic Work, and Energy associated with matter transfer. It also relates each type of energy transfer to a property of a body's Internal Energy. The First L
8 min read
Second Law of ThermodynamicsSecond Law of Thermodynamics defines that heat cannot move from a reservoir of lower temperature to a reservoir of higher temperature in a cyclic process. The second law of thermodynamics deals with transferring heat naturally from a hotter body to a colder body. Second Law of Thermodynamics is one
10 min read
Thermodynamic CyclesThermodynamic cycles are used to explain how heat engines, which convert heat into work, operate. A thermodynamic cycle is used to accomplish this. The application determines the kind of cycle that is employed in the engine. The thermodynamic cycle consists of a series of interrelated thermodynamic
15 min read
Thermodynamic State Variables and Equation of StateThe branch of thermodynamics deals with the process of heat exchange by the gas or the temperature of the system of the gas. This branch also deals with the flow of heat from one part of the system to another part of the system. For systems that are present in the real world, there are some paramete
5 min read
Enthalpy: Definition, Formula and ReactionsEnthalpy is the measurement of heat or energy in the thermodynamic system. It is the most fundamental concept in the branch of thermodynamics. It is denoted by the symbol H. In other words, we can say, Enthalpy is the total heat of the system. Let's know more about Enthalpy in detail below.Enthalpy
12 min read
State FunctionsState Functions are the functions that are independent of the path of the function i.e. they are concerned about the final state and not how the state is achieved. State Functions are most used in thermodynamics. In this article, we will learn the definition of state function, what are the state fun
7 min read
Carnot EngineA Carnot motor is a hypothetical motor that works on the Carnot cycle. Nicolas Leonard Sadi Carnot fostered the fundamental model for this motor in 1824. In this unmistakable article, you will find out about the Carnot cycle and Carnot Theorem exhaustively. The Carnot motor is a hypothetical thermod
5 min read
Heat Engine - Definition, Working, PV Diagram, Efficiency, TypesHeat engines are devices that turn heat energy into motion or mechanical work. Heat engines are based on the principles of thermodynamics, specifically the conversion of heat into work according to the first and second laws of thermodynamics. They are found everywhere, from our cars, power plants to
14 min read
Wave and Oscillation
Introduction to Waves - Definition, Types, PropertiesA wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities in physics, mathematics, and related subjects, commonly described by a wave equation. At least two field quantities in the wave medium are involved in physical waves. Periodic waves occur when variables o
11 min read
Wave MotionWave Motion refers to the transfer of energy and momentum from one point to another in a medium without actually transporting matter between the two points. Wave motion is a kind of disturbance from place to place. Wave can travel in solid medium, liquid medium, gas medium, and in a vacuum. Sound wa
12 min read
OscillationOscillations are defined as the process of repeating vibrations of any quantity about its equilibrium position. The word “oscillation†originates from the Latin verb, which means to swing. An object oscillates whenever a force pushes or pulls it back toward its central point after displacement. This
8 min read
Oscillatory Motion FormulaOscillatory Motion is a form of motion in which an item travels over a spot repeatedly. The optimum situation can be attained in a total vacuum since there will be no air to halt the item in oscillatory motion friction. Let's look at a pendulum as shown below. The vibrating of strings and the moveme
3 min read
Amplitude FormulaThe largest deviation of a variable from its mean value is referred to as amplitude. It is the largest displacement from a particle's mean location in to and fro motion around a mean position. Periodic pressure variations, periodic current or voltage variations, periodic variations in electric or ma
6 min read
What is Frequency?Frequency is the rate at which the repetitive event that occurs over a specific period. Frequency shows the oscillations of waves, operation of electrical circuits and the recognition of sound. The frequency is the basic concept for different fields from physics and engineering to music and many mor
9 min read
Amplitude, Time Period and Frequency of a VibrationSound is a form of energy generated by vibrating bodies. Its spread necessitates the use of a medium. As a result, sound cannot travel in a vacuum because there is no material to transfer sound waves. Sound vibration is the back and forth motion of an entity that causes the sound to be made. That is
5 min read
Energy of a Wave FormulaWave energy, often referred to as the energy carried by waves, encompasses both the kinetic energy of their motion and the potential energy stored within their amplitude or frequency. This energy is not only essential for natural processes like ocean currents and seismic waves but also holds signifi
7 min read
Simple Harmonic MotionSimple Harmonic Motion is a fundament concept in the study of motion, especially oscillatory motion; which helps us understand many physical phenomena around like how strings produce pleasing sounds in a musical instrument such as the sitar, guitar, violin, etc., and also, how vibrations in the memb
15+ min read
Displacement in Simple Harmonic MotionThe Oscillatory Motion has a big part to play in the world of Physics. Oscillatory motions are said to be harmonic if the displacement of the oscillatory body can be expressed as a function of sine or cosine of an angle depending upon time. In Harmonic Oscillations, the limits of oscillations on eit
10 min read
Sound
Production and Propagation of SoundHave you ever wonder how are we able to hear different sounds produced around us. How are these sounds produced? Or how a single instrument can produce a wide variety of sounds? Also, why do astronauts communicate in sign languages in outer space? A sound is a form of energy that helps in hearing to
6 min read
What are the Characteristics of Sound Waves?Sound is nothing but the vibrations (a form of energy) that propagates in the form of waves through a certain medium. Different types of medium affect the properties of the wave differently. Does this mean that Sound will not travel if the medium does not exist? Correct. It will not, It is impossibl
7 min read
Speed of SoundSpeed of Sound as the name suggests is the speed of the sound in any medium. We know that sound is a form of energy that is caused due to the vibration of the particles and sound travels in the form of waves. A wave is a vibratory disturbance that transfers energy from one point to another point wit
12 min read
Reflection of SoundReflection of Sound is the phenomenon of striking of sound with a barrier and bouncing back in the same medium. It is the most common phenomenon observed by us in our daily life. Let's take an example, suppose we are sitting in an empty hall and talking to a person we hear an echo sound which is cre
9 min read
Refraction of SoundA sound is a vibration that travels as a mechanical wave across a medium. It can spread via a solid, a liquid, or a gas as the medium. In solids, sound travels the quickest, comparatively more slowly in liquids, and the slowest in gases. A sound wave is a pattern of disturbance caused by energy trav
5 min read
How do we hear?Sound is produced from a vibrating object or the organ in the form of vibrations which is called propagation of sound and these vibrations have to be recognized by the brain to interpret the meaning which is possible only in the presence of a multi-functioning organ that is the ear which plays a hug
7 min read
Audible and Inaudible SoundsWe hear sound whenever we talk, listen to some music, or play any musical instrument, etc. But did you ever wondered what is that sound and how is it produced? Or why do we hear to our own voice when we shout in a big empty room loudly? What are the ranges of sound that we can hear? In this article,
10 min read
Explain the Working and Application of SONARSound energy is the type of energy that allows our ears to sense something. When a body vibrates or moves in a ‘to-and-fro' motion, a sound is made. Sound needs a medium to flow through in order to propagate. This medium could be in the form of a gas, a liquid, or a solid. Sound propagates through a
8 min read
Noise PollutionNoise pollution is the pollution caused by sound which results in various problems for Humans. A sound is a form of energy that enables us to hear. We hear the sound from the frequency range of 20 to 20000 Hertz (20kHz). Humans have a fixed range for which comfortably hear a sound if we are exposed
8 min read
Doppler Effect - Definition, Formula, ExamplesDoppler Effect is an important phenomenon when it comes to waves. This phenomenon has applications in a lot of fields of science. From nature's physical process to planetary motion, this effect comes into play wherever there are waves and the objects are traveling with respect to the wave. In the re
7 min read
Doppler Shift FormulaWhen it comes to sound propagation, the Doppler Shift is the shift in pitch of a source as it travels. The frequency seems to grow as the source approaches the listener and decreases as the origin fades away from the ear. When the source is going toward the listener, its velocity is positive; when i
3 min read
Electrostatics
ElectrostaticsElectrostatics is the study of electric charges that are fixed. It includes an study of the forces that exist between charges as defined by Coulomb's Law. The following concepts are involved in electrostatics: Electric charge, electric field, and electrostatic force.Electrostatic forces are non cont
13 min read
Electric ChargeElectric Charge is the basic property of a matter that causes the matter to experience a force when placed in a electromagnetic field. It is the amount of electric energy that is used for various purposes. Electric charges are categorized into two types, that are, Positive ChargeNegative ChargePosit
8 min read
Coulomb's LawCoulomb’s Law is defined as a mathematical concept that defines the electric force between charged objects. Columb's Law states that the force between any two charged particles is directly proportional to the product of the charge but is inversely proportional to the square of the distance between t
9 min read
Electric DipoleAn electric dipole is defined as a pair of equal and opposite electric charges that are separated, by a small distance. An example of an electric dipole includes two atoms separated by small distances. The magnitude of the electric dipole is obtained by taking the product of either of the charge and
11 min read
Dipole MomentTwo small charges (equal and opposite in nature) when placed at small distances behave as a system and are called as Electric Dipole. Now, electric dipole movement is defined as the product of either charge with the distance between them. Electric dipole movement is helpful in determining the symmet
6 min read
Electrostatic PotentialElectrostatic potential refers to the amount of electrical potential energy present at a specific point in space due to the presence of electric charges. It represents how much work would be done to move a unit of positive charge from infinity to that point without causing any acceleration. The unit
12 min read
Electric Potential EnergyElectrical potential energy is the cumulative effect of the position and configuration of a charged object and its neighboring charges. The electric potential energy of a charged object governs its motion in the local electric field.Sometimes electrical potential energy is confused with electric pot
15+ min read
Potential due to an Electric DipoleThe potential due to an electric dipole at a point in space is the electric potential energy per unit charge that a test charge would experience at that point due to the dipole. An electric potential is the amount of work needed to move a unit of positive charge from a reference point to a specific
7 min read
Equipotential SurfacesWhen an external force acts to do work, moving a body from a point to another against a force like spring force or gravitational force, that work gets collected or stores as the potential energy of the body. When the external force is excluded, the body moves, gaining the kinetic energy and losing a
9 min read
Capacitor and CapacitanceCapacitor and Capacitance are related to each other as capacitance is nothing but the ability to store the charge of the capacitor. Capacitors are essential components in electronic circuits that store electrical energy in the form of an electric charge. They are widely used in various applications,
11 min read