Orthogonal Sets:
A set of vectors \left \{ u_1, u_2, ... u_p \right \} in \mathbb{R^n} is called orthogonal set, if u_i \cdot u_j =0 . if i \neq j
Orthogonal Basis
An orthogonal basis for a subspace W of \mathbb{R^n} is a basis for W that is also an orthogonal set.
Let S = \left \{ u_1, u_2, ... u_p \right \} be the orthogonal basis for a W of \mathbb{R^n} is a basis for W that is also a orthogonal set. We need to calculate c_1, c_2, ... c_p such that :
y = c_1 u_1 + c_2 u_2 + ... c_p u_p
Let's take the dot product of u_1 both side.
y \cdot u_1 = (c_1 u_1 + c_2 u_2 + ... c_p u_p) \cdot u_1
y \cdot u_1 = c_1 (u_1 \cdot u_1) + c_2 (u_2 \cdot u_1) + ... c_p (u_p \cdot u_1)
Since, this is orthogonal basis u_2 \cdot u_1 = u_3 \cdot u_1 = ... = u_p \cdot u_1 =0 . This gives c_1 :
c_1 = \frac{y \cdot u_1}{ u_1 \cdot u_1}
We can generalize the above equation
c_j = \frac{y \cdot u_j}{ u_j \cdot u_j}
Orthogonal Projections
Suppose {u_1, u_2,... u_n} is an orthogonal basis for W in \mathbb{R^n} . For each y in W:
y =\left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + ... + \left ( \frac{y \cdot u_p}{u_p \cdot u_p } \right )u_p
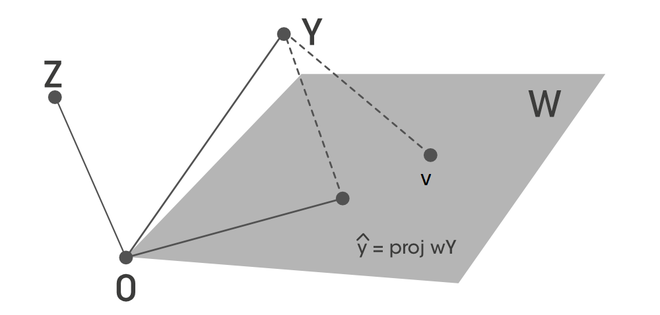
Let's take \left \{ u_1, u_2, u_3 \right \} is an orthogonal basis for \mathbb{R^3} and W = span \left \{ u_1, u_2 \right \} . Let's try to write a write y in the form \hat{y} belongs to W space, and z that is orthogonal to W.
y =\left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + \left ( \frac{y \cdot u_2}{u_2\cdot u_2 } \right )u_2 + \left ( \frac{y \cdot u_3}{u_3 \cdot u_3} \right ) u_3 \\
where
\hat{y} = \left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + \left ( \frac{y \cdot u_2}{u_2\cdot u_2 } \right )u_2
and
z = \left ( \frac{y \cdot u_3}{u_3 \cdot u_3} \right ) u_3 y= \hat{y} + z
Now, we can see that z is orthogonal to both u_1 and u_2 such that:
z \cdot u_1 =0 \\ z \cdot u_2 =0

Orthogonal Decomposition Theorem:
Let W be the subspace of \mathbb{R^n} . Then each y in \mathbb{R^n} can be uniquely represented in the form:
y = \hat{y} + z
where \hat{y} is in W and z in W^{\perp}. If \left \{ u_1, u_2, ... u_p \right \} is an orthogonal basis of W. then,
\hat{y} =\left ( \frac{y \cdot u_1}{u_1 \cdot u_1} \right ) u_1 + ... + \left ( \frac{y \cdot u_p}{u_p \cdot u_p } \right )u_p
thus:
z = y - \hat{y}
Then, \hat{y} is the orthogonal projection of y in W.

Best Approximation Theorem
Let W is the subspace of \mathbb{R^n} , y any vector in \mathbb{R^n} . Let v in W and different from \hat{y} . Then \left \| v-\hat{y} \right \| also in W.
z = y - \hat{y} is orthogonal to W, and also orthogonal to v=\hat{y} . Then y-v can be written as:
y-v = (y- \hat{y}) + (\hat{y} -v)
Thus:
\left \| y-v \right \|^{2} = \left \| y- \hat{y} \right \|^{2} + \left \| \hat{y}-v \right \|^{2}
Thus, this can be written as:
\left \| y-v \right \|^{2} > \left \| y- \hat{y} \right \|^{2}
and
\left \| y-v \right \| > \left \| y- \hat{y} \right \|
References: