A rational number is a type of real number expressed as p/q, where q ≠ 0. Any fraction with a non-zero denominator qualifies as a rational number. Examples include 1/2, 1/5, 3/4, and so forth. Additionally, the number 0 is considered a rational number as it can be represented in various forms such as 0/1, 0/2, 0/3, etc.
In this article, learn about rational numbers, their properties, examples, and others in detail.
What are Rational Numbers?
A rational number is any number that can be written as a simple fraction. This includes all integers, as any integer z can be written as z/1.
Rational Numbers Definition
Rational Number is a real number written in the form of p/q where p and q are integers and q is not equal to zero.
- Rational numbers can be expressed as fractions, decimals, and even zeros.
- All the numbers with a non-zero denominator that can be written in p/q form are rational numbers.
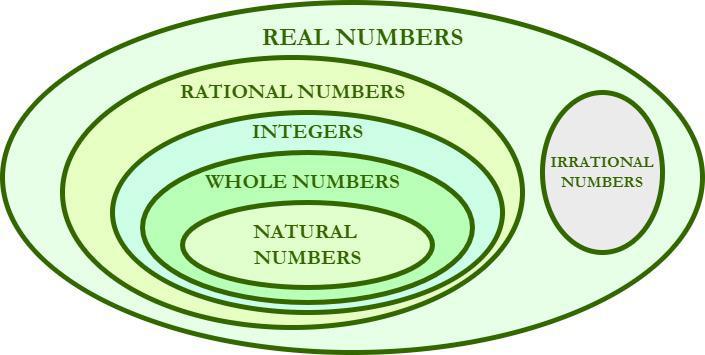
Various types of numbers can be represented as rational numbers some of which are discussed below:
A rational number is a ratio of two integers. Hence, in the fraction number, it can be written in the form of p/q where q is not equal to zero. Hence, any fraction with a non-zero denominator is a rational number.
Example
-2 / 5 is a rational number where -2 is an integer being divided by a non-zero integer 5
A rational number can be also written in the decimal form if the decimal value is definite or has repeating digits after the decimal point.
Example
0.3 is a rational number. As the value 0.3 can be further expressed in the form of ratio or fraction as p/q
0.3 = 3/10
Also, 1.333333... can be represented as 4/3 hence, 1.33333... is a rational number.
The standard form of a rational number is, p/q
where,
- p and q are both integers with no common integers,
- q can never be zero.
For example, 2/6 is a rational number but it is not in its standard form as 2/6 has a common factor of 2 and it can further be simplified as 1/3. Thus, its standard form is 1/3.
Is 0 a Rational Number?
Yes, 0 is a rational number as it has a non-zero denominator. It can be written in the p / q form as,
0 = 0/1 = p / q
Learn, Zero is Rational or Not
How to Identify Rational Numbers?
Rational Numbers have various properties from which we can identify them some of which are given below:
- Natural numbers, Whole Numbers, Fractions, and Integers all are rational numbers.
- All terminating decimals are Rational Numbers.
- All recurring decimals are Rational Numbers.
- All the numbers which can be expressed as p/q where p and q are integers are Rational Numbers.
Note: Non-Recurring and Non Terminating decimals are Irrational Numbers.
Example: Check whether 2.69696969... is a rational number or not?
Solution:
Given Number 2.69696969... has repeating value 69 after decimal hence it is a rational number.
Positive and Negative Rational Numbers
- If the rational number is positive, both p and q are positive integers.
- If the rational number takes the form -(p/q), then either p or q takes the negative value. It means that -(p/q) = (-p)/q = p/(-q)
Addition of Rational Numbers
Let's take two rational numbers p/q and s/t, adding these two using rules of addition we get
p/q + s/t = (pt+qs)/qt
Example: Add 3/5 + 2/7
Solution:
3/5 + 2/7 = (3×7 + 2×5) / 5×7
= (21 + 10) / 35
= 31 / 35
Subtraction of Rational Numbers
Let's take two rational numbers p/q and s/t, subtracting these two using rules of subtraction we get
p/q - s/t = (pt - qs)/qt
Example: Subtract 3/5 - 2/7
Solution:
3/5 - 2/7 = (3×7 - 2×5) / 5×7
= (21 - 10) / 35
= 11 / 35
Multiplication of Rational Numbers
Let's take two rational numbers p/q and s/t, multiplying these two using rules of multiplication we get
p/q × s/t = (p × s) / (q × t)
Example: Multiply 3/5 × 2/7
Solution:
3/5 × 2/7 = (3 × 2) / (5 × 7)
= 6 / 35
Division of Rational Numbers
Let's take two rational numbers p/q and s/t, we know that divide is the inverse of multiply then dividing these two using rules of division we get
(p/q) / (s/t) = p/q × t/s = (p × t) / (q × s)
Example: Divide (3/5) / (2/7)
Solution:
(3/5) / (2/7) = 3/5 × 7/2
= (3 × 7) / (5 × 2)
= 21 / 10
Multiplicative Inverse of Rational Numbers
A Multiplicative Inverse of Rational Numbers is a number that when multiplied by the number results in 1. The general form of a rational number is p/q then its multiplicative inverse is q/p.
For example: For a rational number 2/3, then its multiplicative inverse is 3/2, such that,
2/3 × 3/2 = 1
Properties of Rational Numbers
Various properties of rational numbers are,
- The results are always a rational number if we multiply, add, or subtract any two rational numbers.
- Multiplying or dividing the numerator and denominator of any rational number with the same number does not change the number such that, p/q = ap/aq.
- Multiplication, Division, Addition, and Subtraction of any two rational numbers result in a rational number.
- The additive inverse of the rational number is zero as p/q + 0 = p/q
- The multiplicative inverse of the rational number is 1 as p/q × 1 = p/q
Rational Numbers and Irrational Numbers
Rational Numbers and Irrational Numbers both are subsets of real numbers the basic difference between them is that Rational Numbers can be represented as p/q whereas Irrational Numbers can not be represented as p/q.
An irrational number is a type of real number that cannot be expressed as a ratio of two integers (i.e., it cannot be written in the form p/q, where p and q are integers and q≠0. These numbers have non-repeating, non-terminating decimal expansions.
All natural numbers, whole numbers, decimals, and others are subsets of rational numbers while irrational numbers are those numbers that are non-repeating and non-terminating numbers.
Examples of Rational Numbers
- 1, 2, 3,...
- 1/2, 2/3, 4/5,...
- 2.3 = 23/10, etc.
Examples of Irrational Numbers
- √2 = 1.414213…
- √3 = 1.7320508...
- Pi (π) = 3.142857…
- Euler’s Number (e) = 2.7182818284590452…….
How to Find Rational Numbers Between Two Rational Numbers?
We can find Rational Numbers between Two Rational Numbers by two methods which are,
Method 1
For the given rational numbers find their equivalent rational numbers and then the number between them is found easily.
Example: Find the rational number between 1/2 and 4/3.
Solution:
1/2 = 3/6
4/3 = 8/6
Then rational numbers between 3/6 and 8/6 are 4/6, 5/6, 6/6, 7/6.
Method 2
In the second method, we find the mean of the given two numbers (m) and then find the mean of the first number with m and the mean of the second number with m, and repeated this process to get more numbers.
Example: Find the rational number between 1/2 and 4/3.
Solution:
Mean of 1/2, 4/3 = (1/2 + 4/3) / 2 = 11/12
Mean of 1/2, 11/12 = (1/2 + 11/12) / 2 = 17/24
Mean of 11/12, 4/3 = (11/12 + 4/3) / 2 = 27/24
Then rational numbers between 3/6 and 8/6 are 17/24, 11/12, 27/24.
People Also View:
Solved Examples on Rational Numbers
Example 1: What are the rational numbers between 3 and 5?
Solution:
Rational Numbers between 3 and 5 are 31/10, 32/10, 33/10, 34/10, 35/10, 36/10,..............,49/10
Lets express 3 and 5 as rational numbers as
3 = 3×10/10 = 30/10
5= 5×10/10 = 50/10
Hence, the rational numbers between 3 and 5 are 30/10 and 50/10 are 31/10, 32/10, 33/10, 34/10, 35/10, 36/10, 37/10, 38/10, 39/10, 40/10, ..............49/10.
Example 2: What are the five rational numbers between 0 and 1?
Solution:
Five rational numbers between 0 and 1 are 0.1, 0.2, 0.3, 0.4 and 0.5.
Example 3: Simplify, 1/2 + 2/3 - 4/5
Solution:
1/2 + 2/3 - 4/5
= 7/6 - 4/5
= (35 - 24) / 30 = 9/30
= 3/10
Example 4: Simplify, 1/2 × 2/3 ÷ 4/5
Solution:
1/2 × 2/3 ÷ 4/5
= 1/2 × 2/3 × 5/4
= 5/12
Similar Reads
CBSE Class 8th Maths Notes CBSE Class 8th Maths Notes cover all chapters from the updated NCERT textbooks, including topics such as Rational Numbers, Algebraic Expressions, Practical Geometry, and more. Class 8 is an essential time for students as subjects become harder to cope with. At GeeksforGeeks, we provide easy-to-under
15+ min read
Chapter 1: Rational Numbers
Rational NumbersA rational number is a type of real number expressed as p/q, where q ≠0. Any fraction with a non-zero denominator qualifies as a rational number. Examples include 1/2, 1/5, 3/4, and so forth. Additionally, the number 0 is considered a rational number as it can be represented in various forms such a
9 min read
Natural Numbers | Definition, Examples & PropertiesNatural numbers are the numbers that start from 1 and end at infinity. In other words, natural numbers are counting numbers and they do not include 0 or any negative or fractional numbers.Here, we will discuss the definition of natural numbers, the types and properties of natural numbers, as well as
11 min read
Whole Numbers - Definition, Properties and ExamplesWhole numbers are the set of natural numbers (1, 2, 3, 4, 5, ...) plus zero. They do not include negative numbers, fractions, or decimals. Whole numbers range from zero to infinity. Natural numbers are a subset of whole numbers, and whole numbers are a subset of real numbers. Therefore, all natural
10 min read
Integers | Definition, Examples & TypesThe word integer originated from the Latin word “Integer†which means whole or intact. Integers are a special set of numbers comprising zero, positive numbers, and negative numbers. So, an integer is a whole number (not a fractional number) that can be positive, negative, or zero. Examples of intege
8 min read
Rational NumbersRational numbers are a fundamental concept in mathematics, defined as numbers that can be expressed as the ratio of two integers, where the denominator is not zero. Represented in the form p/q​ (with p and q being integers), rational numbers include fractions, whole numbers, and terminating or repea
15+ min read
Representation of Rational Numbers on the Number Line | Class 8 MathsRational numbers are the integers p and q expressed in the form of p/q where q>0. Rational numbers can be positive, negative or even zero. Rational numbers can be depicted on the number line. The centre of the number line is called Origin (O). Positive rational numbers are illustrated on the righ
5 min read
Rational Numbers Between Two Rational Numbers | Class 8 MathsReal numbers are categorized into rational and irrational numbers respectively. Given two integers p and q, a rational number is of the form p/q, where q > 0. A special case arises when q=1 and the rational number simply becomes an integer. Hence, all integers are rational numbers, equal to p. Th
6 min read
Chapter 2: Linear Equations in One Variable
Algebraic Expressions in Math: Definition, Example and EquationAlgebraic Expression is a mathematical expression that is made of numbers, and variables connected with any arithmetical operation between them. Algebraic forms are used to define unknown conditions in real life or situations that include unknown variables.An algebraic expression is made up of terms
8 min read
Linear Equations in One VariableLinear equation in one variable is the equation that is used for representing the conditions that are dependent on one variable. It is a linear equation i.e. the equation in which the degree of the equation is one, and it only has one variable.A linear equation in one variable is a mathematical stat
7 min read
Linear Equations in One Variable - Solving Equations which have Linear Expressions on one Side and Numbers on the other Side | Class 8 MathsLinear equation is an algebraic equation that is a representation of the straight line. Linear equations are composed of variables and constants. These equations are of first-order, that is, the highest power of any of the involved variables i.e. 1. It can also be considered as a polynomial of degre
4 min read
Solving Linear Equations with Variable on both SidesEquations consist of two main components: variables and numbers. Understanding the relationship between these components and how to manipulate them is essential for solving equations.Variable: A variable is a symbol (often a letter like x, y, or z) that represents an unknown or changing quantity.Num
6 min read
Reducing Equations to Simpler Form | Class 8 MathsReducing equations is a method used to simplify complex equations into a more manageable form. This technique is particularly useful when dealing with non-linear equations, which cannot always be solved directly. By applying specific mathematical operations, such as cross-multiplication, these equat
6 min read
Equations Reducible to Linear FormEquations Reducible to Linear Form" refers to equations that can be transformed or rewritten into a linear equation. These equations typically involve variables raised to powers other than 1, such as squared terms, cubed terms, or higher. By applying suitable substitutions or transformations, these
9 min read
Chapter 3: Understanding Quadrilaterals
Types of PolygonsTypes of Polygons classify all polygons based on various parameters. As we know, a polygon is a closed figure consisting only of straight lines on its edges. In other words, polygons are closed figures made up of more than 2 line segments on a 2-dimensional plane. The word Polygon is made up of two
9 min read
Triangles in GeometryA triangle is a polygon with three sides (edges), three vertices (corners), and three angles. It is the simplest polygon in geometry, and the sum of its interior angles is always 180°. A triangle is formed by three line segments (edges) that intersect at three vertices, creating a two-dimensional re
13 min read
QuadrilateralsQuadrilateral is a two-dimensional figure characterized by having four sides, four vertices, and four angles. It can be broadly classified into two categories: concave and convex. Within the convex category, there are several specific types of quadrilaterals, including trapezoids, parallelograms, re
12 min read
Area of PentagonArea of Pentagon or the area of any polygon is the total space taken by that geometric object. In geometry area and perimeter are the most fundamental quantities of measurement after the side. In general, we study two types of shapes in geometry one is flat shapes(2-D Shapes) and other solid shapes
7 min read
Sum of Angles in a PolygonPolygon is defined as a two-dimensional geometric figure that has a finite number of line segments connected to form a closed shape. The line segments of a polygon are called edges or sides, and the point of intersection of two edges is called a vertex. The angle of a polygon is referred to as the s
11 min read
Exterior Angles of a PolygonPolygon is a closed, connected shape made of straight lines. It may be a flat or a plane figure spanned across two-dimensions. A polygon is an enclosed figure that can have more than 3 sides. The lines forming the polygon are known as the edges or sides and the points where they meet are known as ve
6 min read
Trapezium: Types | Formulas |Properties & ExamplesA Trapezium or Trapezoid is a quadrilateral (shape with 4 sides) with exactly one pair of opposite sides parallel to each other. The term "trapezium" comes from the Greek word "trapeze," meaning "table." It is a two-dimensional shape with four sides and four vertices.In the figure below, a and b are
8 min read
Kite - QuadrilateralsA Kite is a special type of quadrilateral that is easily recognizable by its unique shape, resembling the traditional toy flown on a string. In geometry, a kite has two pairs of adjacent sides that are of equal length. This distinctive feature sets it apart from other quadrilaterals like squares, re
8 min read
Parallelogram | Properties, Formulas, Types, and TheoremA parallelogram is a two-dimensional geometrical shape whose opposite sides are equal in length and are parallel. The opposite angles of a parallelogram are equal in measure and the Sum of adjacent angles of a parallelogram is equal to 180 degrees.A parallelogram is a four-sided polygon (quadrilater
10 min read
Properties of ParallelogramsProperties of Parallelograms: Parallelogram is a quadrilateral in which opposite sides are parallel and congruent and the opposite angles are equal. A parallelogram is formed by the intersection of two pairs of parallel lines. In this article, we will learn about the properties of parallelograms, in
9 min read
Rhombus: Definition, Properties, Formula and ExamplesA rhombus is a type of quadrilateral with the following additional properties. All four sides are of equal length and opposite sides parallel. The opposite angles are equal, and the diagonals bisect each other at right angles. A rhombus is a special case of a parallelogram, and if all its angles are
6 min read
Square in Maths - Area, Perimeter, Examples & ApplicationsA square is a type of quadrilateral where all four sides are of equal length and each interior angle measures 90°. It has two pairs of parallel sides, with opposite sides being parallel. The diagonals of a square are equal in length and bisect each other at right angles.Squares are used in various f
5 min read
Chapter 4: Practical Geometry
Chapter 5: Data Handling
Data HandlingData Handling: Nowadays, managing and representing data systematically has become very important especially when the data provided is large and complex, This is when Data Handling comes into the picture.Data handling involves the proper management of research data throughout and beyond the lifespan
12 min read
What is Data Organization?It is a critical process that involves structuring, categorizing, and managing data to make it more accessible, usable, and analyzable. Whether in research, business, or everyday applications, well-organized data can significantly enhance efficiency and decision-making. The importance of data organi
9 min read
Frequency Distribution - Table, Graphs, FormulaA frequency distribution is a way to organize data and see how often each value appears. It shows how many times each value or range of values occurs in a dataset. This helps us understand patterns, like which values are common and which are rare. Frequency distributions are often shown in tables or
11 min read
Pie ChartPie chart is a popular and visually intuitive tool used in data representation, making complex information easier to understand at a glance. This circular graph divides data into slices, each representing a proportion of the whole, allowing for a clear comparison of different categories making it ea
11 min read
Chance and ProbabilityChance is defined as the natural occurrence of any event without any interference, we can also say that the possibility of any event is the chance of the event, and mathematically we define the chance as the probability of an event.Probability refers to the likelihood of the occurrence of an event.
9 min read
Random Experiment - ProbabilityIn a cricket match, before the game begins. Two captains go for a toss. Tossing is an activity of flipping a coin and checking the result as either “Head†or “Tailâ€. Similarly, tossing a die gives us a number from 1 to 6. All these activities are examples of experiments. An activity that gives us a
11 min read
Probability in MathsProbability is the branch of mathematics where we determine how likely an event is to occur. It is represented as a numeric value ranging from 0 to 1. Probability can be calculated as:\text{Probability} = \dfrac{Favourable \ Outcome}{Total \ Number \ of \ Outcomes}Favourable outcomes refer to the ou
4 min read
Chapter 6: Squares and Square Roots
Chapter 7: Cubes and Cube Roots
Chapter 8: Comparing Quantities
Ratios and PercentagesRatios and Percentages: Comparing quantities is easy, each of the quantities is defined to a specific standard and then the comparison between them takes place after that. Comparing quantities can be effectively done by bringing them to a certain standard and then comparing them related to that spec
6 min read
Fractions - Definition, Types and ExamplesFractions are numerical expressions used to represent parts of a whole or ratios between quantities. They consist of a numerator (the top number), indicating how many parts are considered, and a denominator (the bottom number), showing the total number of equal parts the whole is divided into. For E
7 min read
PercentageIn mathematics, a percentage is a figure or ratio that signifies a fraction out of 100, i.e., A fraction whose denominator is 100 is called a Percent. In all the fractions where the denominator is 100, we can remove the denominator and put the % sign.For example, the fraction 23/100 can be written a
5 min read
Discount FormulaDiscount in Mathematics is defined as the reduction in price of any service and product. Discount is offered by the business owner to easily and quickly sell their product or services. Giving discounts increases the sales of the business and helps the business retain its customer. Discount is always
9 min read
Sales Tax, Value Added Tax, and Goods and Services Tax - Comparing Quantities | Class 8 MathsTax is a mandatory fee levied by the government to collect revenue for public works providing the best facilities and infrastructure.The first known Tax system was in Ancient Egypt around 3000–2800 BC, in First Dynasty of Egypt. The first form of taxation was corvée and tithe. In India, The Tax was
5 min read
Simple InterestSimple Interest (SI) is a method of calculating the interest charged or earned on a principal amount over a fixed period. It is calculated based solely on the principal amount, which remains unchanged throughout the calculation.Simple Interest is widely used across industries such as banking, financ
9 min read
Compound Interest | Class 8 MathsCompound Interest: Compounding is a process of re-investing the earnings in your principal to get an exponential return as the next growth is on a bigger principal, following this process of adding earnings to the principal. In this passage of time, the principal will grow exponentially and produce
9 min read
Compound InterestCompound Interest is the interest that is calculated against a loan or deposit amount in which interest is calculated for the principal as well as the previous interest earned. Compound interest is used in the banking and finance sectors and is also useful in other sectors. A few of its uses are:Gro
9 min read
Chapter 9: Algebraic Expressions and Identities
Algebraic Expressions and IdentitiesAn algebraic expression is a mathematical phrase that can contain numbers, variables, and operations, representing a value without an equality sign. Whereas, algebraic identities are equations that hold true for all values of the variables involved. Learning different algebraic identities is crucial
10 min read
Types of Polynomials (Based on Terms and Degrees)Types of Polynomials: In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. There are mainly four types of polynomials based on degree-constant polynomial (zero degree), linear polynomial ( 1st degree), quadratic polynomial (2n
9 min read
Like and Unlike Algebraic Terms: Definition and ExamplesLike terms are terms in algebraic expressions that have the same variables raised to the same powers. Like and Unlike Terms are the types of terms in algebra, and we can differentiate between like and unlike terms by simply checking the variables and their powers. We define algebraic terms as the in
7 min read
Mathematical Operations on Algebraic Expressions - Algebraic Expressions and Identities | Class 8 MathsThe basic operations that are being used in mathematics (especially in real number systems) are addition, subtraction, multiplication and so on. These operations can also be done on the algebraic expressions. Let us see them in detail. Algebraic expressions (also known as algebraic equations) are de
5 min read
Multiplying PolynomialsPolynomial multiplication is the process of multiplying two or more polynomials to find their product. It involves multiplying coefficients and applying exponent rules for variables.When multiplying polynomials:Multiply the coefficients (numerical values).Multiply variables with the same base by add
8 min read
Standard Algebraic IdentitiesAlgebraic Identities are algebraic equations that are always true for every value of the variable in them. The algebraic equations that are valid for all values of variables in them are called algebraic identities. It is used for the factorization of polynomials. In this way, algebraic identities ar
7 min read