Vertical Angles are the angles lying opposite to each other when two lines intersect. Vertical Angles are always equal to each other. Intersecting lines generate sets of vertical angles with different characteristics. Two vertical angles have a common vertex, but these vertical angles have no common sides however between various geometric configurations they share the same measure.
In this article, we will explore vertical angles, vertical angles definition, vertical angles examples, and vertical angles theorem.

Facts About Vertical Angles |
|---|
Vertical Angles are formed when the two lines intersect. |
Vertical Angles share a common vertex. |
They form an 'X' shape. |
Vertical Angles in both pairs sum up to 360°. |
Vertical Angles Meaning
When two lines meet at a point, the angle formed between them is called vertical. The latter are always equal to the former. That is to say, wherever two lines cut each other there are 4 angles. From this, we can clearly see that the two opposite angles are equal, and these areas complement each other to be called vertical angles.
Read, Vertically Opposite Angles
Vertical Angles Definition
Vertical angles can be defined as those angles that lie opposite each other when two lines intersect. Two vertical angles always share a common vertex. However, they never share a common side (arm). For example, ∠1 and ∠3 are vertical angles.

Vertical Angle Examples
Vertical Angle Examples are mentioned below
- Intersecting Lines: Think of two straight lines crossing each other. Opposite angles at the point of intersection are vertical angles.
- Real-Life Scenarios: Two roads intersecting at angles that form vertical angles.
- Book Arrangement: Imagine two books open lying in an "L" shape. Pages where the books interact give rise to vertical angles.
- Open Scissors: When you open a pair of scissors and look at the angle between its two blades, that's a set of vertical angles.
- Intersecting Beams of Light: When the beams cross, they make vertical angles. And if one beam of light is tilted by 30 degrees, then the vertical angle of the other will be exactly 30 degrees.
- Intersecting Bars: When two beams or bars cross, the angles at their points of intersection are called vertical angles. For example, if a horizontal beam runs across the top of vertical one, angles which meet at their intersection form pairs of vertices.
- X-Shaped Structure: Take for example a structure in the form of an "X" made up by two crossing lines. A: At the center of the X, these are vertical angles. If one angle in the center is 120 degrees, its vertical angle counterpart will be too.
- Meeting Paths: Imagine two paths crossing in a park or on an atlas. The angles formed where the paths cross each other are vertical angles.
History of Vertical Angles
History of vertical angles formed by crossing lines have a long history in geometry, extending back to the first beginnings. There may not be any particular historical record which describes the discovery or explanation of vertical angles, but they have been recognized in connection with mathematical thought and geometry.
The Babylonians, Egyptians and Greeks made great advances in geometry and spatial relationships thousands of years ago. Many people call Euclid, the father of geometry (or geometria), who was active around 300 BCE and, in whose Elements, he systematized key geometric principles. Additionally, this work set the stage for later discoveries concerning vertical angles through its discussions of angles and lines and their points where they meet.
Vertical Angles Theorem
The vertical angles theorem simply says that when two parallel lines intersect, the two opposite angles are always equal. The vertical angles theorem Let's take a look at the proof in detail.
Vertical Angle Theorem Statement
Vertical angles (the opposite angles that are formed when two lines intersect each other) are congruent.
Vertical Angles Proof
The proof is simple and based on straight angles. We already know that the sum of angles on a straight line is 180°.
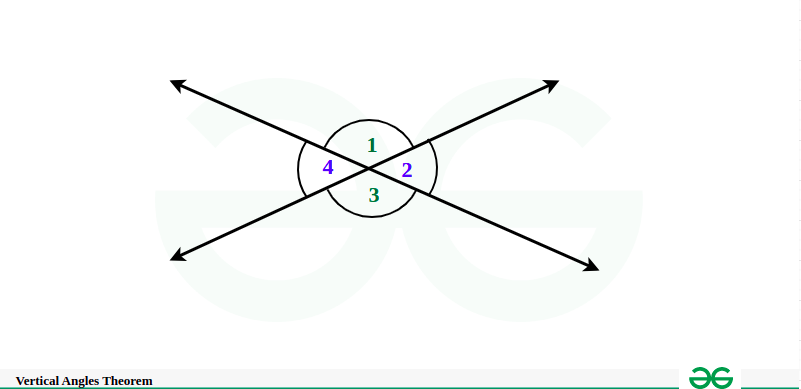
So, in the above figure,
∠1 +∠2 = 180° (Since they are a linear pair of angles, their sum must equal to an angle of 180°) _______ (1)
∠1 +∠4 = 180° (Because they are a linear pair of angles) __________ (2)
That is, from equations (1) and (2), ∠1 + ∠2 = 180° = ∠1 +∠4.
For instance, if a = b and b = c then according to the transitive property of equations we know that a = c.
Hence the above may be restated as ∠1 + ∠2 = ∠1 +∠4. _________ (3)
Cross multiplying ∠1 from both sides of equation (3), we find that ∠2 = ∠4.
Similarly. The same series of statements can be employed to demonstrate that ∠1 = ∠3. Hence, we can say that angles vertically opposite are always equal.
Since its angle-into the figure is a straight angle, and since it emits two vertical angles (opposite sides), we employ both principles--the property of a straight angle together with horizontal line beam.
Vertical Angles in a Triangle
When a transversal (a line that intersects two other lines) passes through the sides of a triangle, producing several angles, vertical angles thereby enter into play. These vertical angles have specific relationships within the triangle:
- Adjacent Angles in a Triangle: Take, for instance a triangle with one side extended into a straight line. This extension forms an exterior angle. This exterior angle has adjacent interior angles in the triangle. These latter are called verticals to the interior angles of any triangle.
- Vertical Angles and Triangle Interior Angles: A transversal line cutting through two sides of a triangle produces vertical angles in pairs. These vertical angles are the interior angles of the triangle.
- Sum of Interior Angles: The sum of the interior angles on a triangle remains at 180°. If a transversal line intersects the sides of a triangle, this sum includes vertical angles.
- Triangle Intersections: When several triangles have a common vertex or side, the angles at these intersections will still possess some vertical angle properties even if it is not in this narrow sense of two lines meeting.
- Exterior Angles: If one side of the triangle is extended, then 'the exterior angle' creates vertical angles with remote interior angles. As for their relationships with interior angles, these exterior angles resemble verticals in the same way that they do in terms of measure.
- Altitude and Base Angles: If an altitude is drawn from a vertex to the opposite side of a triangle, two right angles are formed. These right angles are with respect to one another like vertical angles, in that they're congruent and have a common vertex. They have a relationship similar to that of the vertical angles formed by intersecting lines.
- Triangle Exterior and Interior Angles: If the side of a triangle is extended to form an exterior angle, it can be regarded as being in much the same relationship with the interior angles as two vertical lines. Many cases show there is a parallel in measures, with the exterior angle equal to the sum of the two remote interior angles.
- Triangle Intersections in Polygons: The intersections of their sides or vertices are often angle relationships similar to vertical angles. This is particularly true when one has the various triangles sharing common vertices and sides.
Applications of Vertical Angles
There are many practical applications of vertical angles that we can observe in daily life.
- They are also adjusting the roller coasters at a particular angle for operation. They are so important, in fact, that if these angles were moved up or down a degree there could be an accident. The greatest vertical angle allowed is 112 degrees for the Mumbo Jumbo roller coaster at Flamingo Land.
- When we go to an airshow, we see two vapor trails stabbing into each other like a cross.
- X for safety of vehicles? Railroad crossing signs put up on roads.
- The kite itself is a cross between two wooden sticks.
- There are 10 pairs of vertical angles around the dartboard, with a virtual cross in front.
Read More About
Vertical Angles - Solved Examples
Example 1: Find the missing angles in this shape below.

Solution:
Angle 47 and angle b are vertical angles. So, angle b is also 47° (vertical angles have the same size).
Angle 47 degrees and angle a are angles that add up to 180. Therefore, ∠a = 180° – 47°
⇒ ∠a = 133°
Angle a and angle c are called vertical angles. Hence, ∠ c = 133°
Example 2: Find the angle θ in the picture given.

Solution:
Looking at the picture given above, θ+20° and x are sides that go straight up. Therefore,
Angle (θ + 20)° equals angle x.
But 110° plus x equals 180° (angles that add up to a straight line).
x = (180 – 110) °
⇒ x = 70°
Replace x with 70 in the equation.
⇒ ∠ (θ + 20) ° equals to an angle of about 70°.
⇒ θ = a little over halfway between 70 and 20, which is roughly about equal to the number of fingers on one hand.
So, the value of θ is 50°.
Example 3: Find the size of angle y in the drawing given below.

Solution:
140° + z = 180°
⇒ z = 180° – 140°
⇒ z = 40°
But (x + y) plus z equals 180°.
Adding x and y, then adding 40° is equal to 180°.
x + y = 140°
⇒ 90° + y = 140°
⇒ y = 50°
Example 4: If 100 and (3x + 7) are vertical angles, find the value of x.
Solution:
Vertical angles are equal, therefore;
(3x + 7)° = 100°
⇒ 3x = 100 – 7
⇒ 3x = 93
⇒ x = 31°
So, the value of x is 31°.
Example 5: Given that both AOB and DOC are straight lines. Find X.

Solution:
Angle AOC equals angle DOB - used for vertical angles
⇒ q + 45˚= 135˚
⇒ q = 90˚.
Vertical Angles - Practice Questions
Q1: Angle A is 50°, what's the measure of its vertical angle?
Q2: In a pair of vertical angles, if one measures 120° what is the measure of its angle?
Q3: If angle A measures 50°, how big is the measurement of its vertical?
Q4: If the measure of one angle in a pair of vertical angles is 120°, what is its vertical angle?
Q5: Take two intersecting lines to make four angles. What is the measurement of its vertical angle if one of them measures 110°?
Q6: In a triangle: If one angle is 60°, what about the vertically-opposite?
Q7: What is the relationship between exterior angles and interior angles of a triangle; what parallels does this show to vertical edges?