Coordinate Axes are the fundamental concept in Coordinate Geometry, which is the combination of two branches of mathematics, i.e., algebra and geometry. The basic idea of coordinate geometry is to study the properties of various figures in mathematics, i.e., points, lines, curves, etc.
Thus, Coordinate Axes form the basis of coordinate geometry, which is the branch of mathematics dealing with the plotting of points, lines, and curves on the coordinate axes system or the Euclidean plane. In this article, we will learn about the Coordinate Axes in detail.
.webp)
What are Coordinate Axes?
In any plane, we need a certain number of lines to represent the position of a point in the plane. These lines are called coordinate axes. For example, we need 2 coordinate axes to represent a point in the 2D plane. The plane that is formed by the intersection of these axes is called the Cartesian plane.
History of Coordinate Axes
Rene Descartes is credited for the discovery of the coordinate axes as well as the Cartesian coordinate system. In ancient times, there was no overlapping of algebra and geometry but Rene showed the world that various concepts of algebra and geometry can be studied with the help of each other. Rene came up with the idea of coordinate axes when he observed a fly crawling in a crisscross manner across the beams of his ceiling.
Thus world was now introduced to a fusion of algebra and geometry. The development of coordinate geometry also led to the development of calculus in future and the concept of 2D coordinate axes further laid the foundation for development of vector spaces.
Coordinate Axes in Two Dimension
In 2 dimensional plane, a point is located using its distance from the two coordinate axes. These axes are perpendicular to each other always. Thus coordinate axes in two dimension helps us determine the position of the point in terms of the length and width of the projections of the point on each coordinate axis.
There are two axis in the two dimension coordinate system,
X-axis and Y-axis
Cartesian coordinate system in 2 dimensions uses two axes to show a point in 2 dimensional space. These axes are X-axis and Y-axis . These axes are placed perpendicular to each other. X-axis is the horizontal axis and Y-axis is the vertical axis. The point of intersection of X-axis and Y-axis is called Origin.
Each point in the cartesian coordinate system is determined using its x and y coordinate and represented as (x, y). The Origin is represented using O(0, 0). The X-axis is divided into two parts by the origin i.e. OX and OX'. OX' is used to show numbers with negative X coordinate. Similarly Y-axis is divided into two parts by the origin i.e. OY and OY'. OY' is used to show numbers with negative Y coordinate.
Quadrants and Sign Convention
The XX' and YY' intersect at origin and this results in the formation of 4 quadrants as shown in the below diagram:

- The region XOY is the First Quadrant.
- In first quadrant, both x and y coordinate are positive i.e . (+, +).
- The region X'OY is the Second Quadrant.
- In second quadrant, x coordinate is negative and y coordinate is positive i.e. (-, +).
- The region X'OY' is the Third Quadrant.
- In third quadrant, both x and y coordinate are negative i.e. (-, -).
- The region XOY' is the Fourth Quadrant.
- In fourth quadrant, x coordinate is positive and y coordinate is negative i.e. (+, -).
Representing a Point On Coordinate Axes
A point is represented on coordinate axes using its x coordinate and y coordinate. The X coordinate is called abscissa and the Y coordinate is called ordinate. A point P is represented as P(x, y) as shown in the below figure:

In the above figure point P is shown on the Coordinate axes system. The length OR represents the abscissa and length OS represents ordinate of point P.
If the abscissa of a point is zero then it will lie on the YY' and if the ordinate of a point is zero then it will lie on XX'.
Coordinate Axes in Polar Coordinate System
In polar coordinate system , the point is represented using two values which are its distance from the origin or the reference point and an angle from the reference direction. Thus the system that shows a point by its distance and angle from a reference is called polar coordinate system.
Polar Axes and Origin
In the polar coordinate system, origin is termed as pole. Compared to the normal coordinate grid, the polar coordinate system uses a series of concentric circles around the pole. The axes are represented similarly as in the normal coordinate system. A point in polar coordinate system is represented as P(r, θ) where r is the distance of point from the pole and θ is the angle made by the line joining the point and the pole with the reference direction. The concentric circles have a difference of 1 unit in their radius.
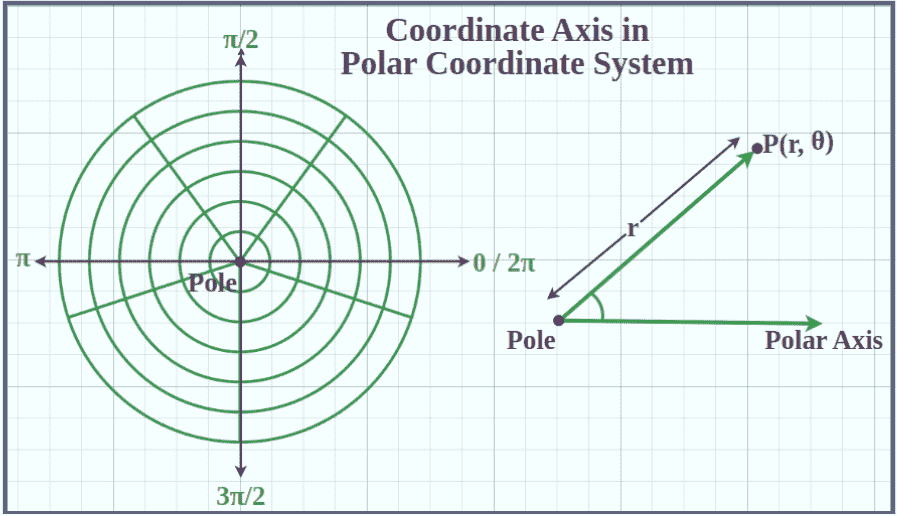
Coordinate Axes in Three Dimensions
We have learnt about representing a point in 2D plane but in real life we generally deal with 3D planes. Hence we need an additional parameter i.e. height of the point to locate it in the 3D plane. Thus we make use of 3 coordinate axes to represent the point in the plane.
X-axis, Y-axis, and Z-axis
Cartesian coordinate system in 3 dimensions uses three axes to show a point in 3 dimensional space. These axes are X-axis, Y-axis and Z-axis. Similar to 2D plane, these axes are placed mutually perpendicular to each other. X-axis is the horizontal axis and Y-axis is the vertical axis. Z-axis is generally represented as the third axis mutually perpendicular to the X and Y axis. The point of intersection of X-axis, Y-axis and Z-axis in 3D plane is called the Origin.

Each point in the 3D cartesian coordinate system is determined using its x, y and z coordinate and represented as (x, y, z). The Origin is represented using O(0, 0, 0). The X-axis is divided into two parts by the origin i.e. OX and OX'. OX' is used to show numbers with negative X coordinate. Similarly Y-axis is divided into two parts by the origin i.e. OY and OY'. OY' is used to show numbers with negative Y coordinate. Similarly Z-axis is divided into two parts by the origin i.e. OZ and OZ'. The origin also divides the entire 3D plane in eight equal parts called octants.
Coordinate Axes in Other Coordinate Systems
Apart from all these coordinate axes systems, there are other coordinate system also. These are:
- Cylindrical Coordinate System
- Spherical Coordinate System
Cylindrical Coordinate System
Cylindrical coordinate system is a combination of the normal coordinate system and the polar coordinate system. a point in cylindrical coordinate system is represented using three quantities i.e. radial distance r, azimuthal angle θ, and the height z of the point from a plane. Thus a point P is represented as P(r, θ, z).
The radial distance r is the distance of the projection of point P (say the projection is represented using Q) in the XY plane from the origin. Azimuthal angle θ is the angle between X-axis and the line joining origin and Q. Height h is the distance of the point from XY plane.
Spherical Coordinate System
Cylindrical coordinate system is used to represent a point on 3D plane. A point in spherical coordinate system is represented using three quantities i.e. radial distance r, polar angle θ, and the azimuthal angle φ. Thus a point P is represented as P(r, θ, φ).
The radial distance r is the distance of the point P from the origin. Radial angle θ is the angle between X-axis and the line joining origin and Q. Azimuthal angle ???? is the angle between Z-axis and the line joining the origin and point P.
Applications of Coordinate Axes System
The system of coordinate axes finds application in various fields such as:
- It is used to locate a place on the surface of the Earth in the form of longitudes and latitudes.
- It is also used in navigation system such as Google Maps to determine the coordinates of a person and the places.
- It can be used to location of one object with respect to the other.
Solved Problems on Coordinate Axes
Problem 1: Identify the quadrant in which the point A(5, -4) lie.
As the abscissa of the point is positive and ordinate is negative, the point A(5, -4) will lie in fourth quadrant.
Problem 2: How will a point having abscissa as 2 and ordinate as 7 and lying in third quadrant be represented?
As the point lies in third quadrant, abscissa and ordinate both will be negative. Thus the point will be represented as (-2, -7).
Problem 3: On which axis will a point having abscissa as 4 and ordinate as 0 and lying in first quadrant lie?
As the point has ordinate as 0, it means that the point will lie on XX' i.e. X-axis.
Problem 4: Identify the quadrant in which the point A(1, 1) lie.
As the abscissa of the point is positive and ordinate is positive, the point A(1, 1) will lie in first quadrant.
Problem 5: How will a point having abscissa as 8 and ordinate as 3 and lying in second quadrant be represented?
As the point lies in second quadrant, abscissa will be negative and ordinate will be positive. Thus the point will be represented as (-2, 7).
Practice Questions on Coordinate Axis
Problem 1: Identify the quadrant in which the point B(−3, 5) lies.
Problem 2: How will a point having abscissa as -2 and ordinate as -6, and lying in the second quadrant, be represented?
Problem 3: On which axis will a point having abscissa as 0 and ordinate as 5 lie?
Problem 4: Identify the quadrant in which the point C(−4, −3) lies.
Problem 5: How will a point having abscissa as -8 and ordinate as 3 and lying in the fourth quadrant be represented?
Similar Reads
Coordinate Geometry Formulas Coordinate geometry or also known as Cartesian geometry is a study of geometry related to using the coordinate points to plot different geometrical shapes like line, curve, triangle, parabola, hyperbola, etc. The points are plotted on a plane using an ordered pair of numbers.Coordinate geometry is u
4 min read
Coordinate Geometry Coordinate geometry is a branch of mathematics that combines algebra and geometry using a coordinate plane. It helps us represent points, lines, and shapes with numbers and equations, making it easier to analyze their positions, distances, and relationships. From plotting points to finding the short
3 min read
GRE Algebra | Coordinate Geometry | Set 2 Prerequisite - GRE Algebra | Coordinate Geometry Geometry is the branch of mathematics that is concerned with property and relation between points, lines, solids, surfaces, and high dimensional objects. Coordinate geometry is the branch of mathematics that deals with two-dimensional figures i.e. x-a
5 min read
Coordinate Axes and Coordinate Planes in 3D space In a plane, we know that we need two mutually perpendicular lines to locate the position of a point. These lines are called coordinate axes of the plane and the plane is usually called the Cartesian plane. But in real life, we do not have such a plane. In real life, we need some extra information su
6 min read
Mid Point Formula in Coordinate Geometry Mid point formula in coordinate geometry provides a way to find the mid point of a line segment when the coordinates of the starting and ending points ( i.e. (x1, y1) and (x2, y2) )of the line segment is known. The mid point divides the line in two equal halves i.e the ratio of the sections of the l
6 min read