Antilog Table in math is a refrence tool used to reverse logarithmic computation and retrieve the original number from its logarithmic value.
- It typically provides a pre-computed antilogarithm value for various logarithmic inputs, commonly in base 1o or natural logarithm base( e.g ≅ 2.71828)
- Antilog table allows users to find the number corresponding to a given logarithmic value without performing complex exponential calculations, as the result can be directly read from the table.
Before the widespread use of calculators and computers, antilog tables were frequently used alongside log tables to simplify calculations involving exponentiation, enabling quick conversion from logarithm results back to standard numerical values.
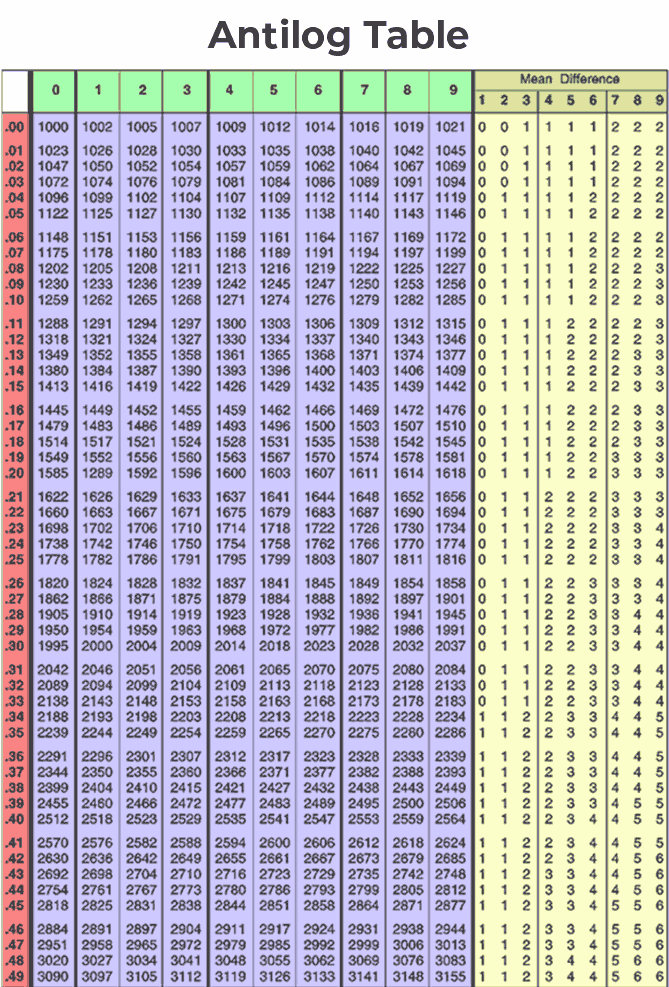

Antilog Table is a mathematical reference tool used to calculate the values of Antilogarithms, which are logarithmic inverse operations. The antilog table consist of list of value, each of which corresponds to the algorithm (10 raised ro the power of) of certain decimal vale.
Antilog Table PDF
Click here to download the PDF version of the Antilog table:
Calculation of Antilog
The logarithm of any number can be divided into two parts: the characteristic and the mantissa. These components help us calculate the value of the antilogarithm for any given logarithmic value.
To calculate the antilogarithm (also known as the inverse logarithm) using the characteristic and mantissa, you need to understand the structure of a logarithmic number. A logarithm can be represented as:
Log(x) = Characteristic + Mantissa
Here,
- Log(x) is the logarithm of the number you want to find the antilogarithm for.
- Characteristic is the integer part of the logarithm, and
- Mantissa is the fractional part of the logarithm.
To find the antilogarithm, we need to calculate,
x = 10 Log(x)
Let's consider an example to understand it better.
Example: Find antilog(2.4567).
Solution:
Let's us assume Log(x) = 2.4567, [Where x is the antilog of 2.4567]
Here, Characteristic = 2 (integer part)
Mantissa = 0.4567 (fractional part)
x = 102 × 100.4567 [100.4567 ≈ 3.016]
⇒ x = 100 × 3.016
⇒ x = 301.6
So, the antilog(2.4567) is approximately 301.6.
How to Use the Antilog Table?
Calculating the Antilog using an Antilog table involves breaking down the given logarithm into its characteristic and mantissa parts. Let's walk through the steps to calculate the Antilog of the number 1.4317 using an Antilog table:
Step 1: Given logarithm: 1.4317.
Separate the integral part (characteristic) from the fractional part (mantissa):
- Characteristic: 1
- Mantissa: 0.4317
Step 2: Find the equivalent value of mantissa using the antilog table. Find the row number that equals .43 and then select column number 1 is the matching value.

Step 3: Proceed to the mean difference column. Use the .56 row again and get the appropriate value in column 8. The value in this case is 7.
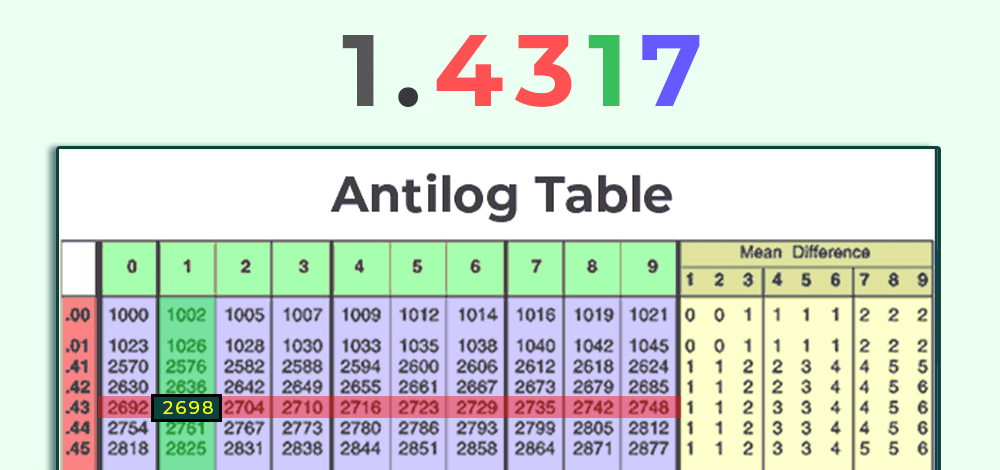
Step 4: Add the values you discovered in steps 2 and 3. It is 2698 + 7 = 3697 in this case.

Step 5: Insert the decimal point now. The decimal point always goes in the correct position. You must multiply the characteristic value by 1. You now have 3. Then, after 3 digits, add the decimal point to obtain 369.7.
As a result, the antilog value of 2.5678 is 369.7.
Calculate Antilog using a Calculator
Using a calculator to calculate the Antilogarithm is a simple technique. Most scientific calculators contain a specific button for calculating Antilogarithms, which is typically labelled "10x" or "antilog." Thus, you can use the following steps to find antilog with any scientific calculator.
- Step 1: Use a scientific calculator with an "antilog" or "10x" button.
- Step 2: Input the given logarithm.
- Step 3: Calculate the antilog using the "10x" button on the calculator.
Antilog from 1 to 10
The following table represents the value of antilog from 1 to 10.
x | Antilog(x) = 10x |
|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1,000 |
| 4 | 10,000 |
| 5 | 100,000 |
| 6 | 1,000,000 |
| 7 | 10,000,000 |
| 8 | 100,000,000 |
| 9 | 1,000,000,000 |
| 10 | 10,000,000,000 |
Antilog vs Log Table
Antilog and Log Tables are both valuable reference tables in mathematics, as well as in physics and chemistry. They are used to manually calculate complex calculations involving exponentials and logarithms.
However, there are some key differences between the two tables, and these differences are listed as follows:
| Aspect | Antilog Table | Log Table |
|---|
| Purpose | Helps find the original number from its logarithm (antilog = 10x). | Helps find the logarithm (log10x or lnx) of a given number. |
|---|
| Content | Contains values that are exponentials of the logarithm. Values. | Contains logarithmic values, typically base 10 or base e (natural logarithm). |
|---|
| Usage | Used to reverse a logarithmic operation or perform exponentiation. | Used to perform logarithmic operations or find the result of such operations. |
|---|
| Example | If you have log base 10 of 2 (log10(2)), you can find the antilog, which is 102 = 100. | If you have a numerical value like 100, you can find its logarithm, which is log base 10 of 100, i.e., log10(100) = 2. |
|---|
| Application | Commonly used in calculations involving exponential growth or decay. | Commonly used in mathematics, engineering, and science for various calculations involving orders of magnitude, exponentiation, and more. |
|---|
Read More,
Important Notes on Antilog Table:
- The Antilog Table gives the value of 10x for the mantissa, with columns for different decimal places.
- The Antilog of a number has two parts: Characteristic (Integral Part) and Mantissa ( Decimal Part).
- We can spilt the number into two parts, use the table for decimal part, and the whole number part.
- The table helps simplify calculations by avoiding the direct computation of powers of 10.
Solved Example of Antilog Table
Example 1: Calculate the antilog of 2.7845.
Solution:
Certainly, let's go through the steps to calculate the Antilogarithm for the given logarithm 2.7845 using the method you've provided:
Step 1: Given logarithm: 2.7845.
Separate the integral part (characteristic) from the fractional part (mantissa):
- Characteristic: 2
- Mantissa: 0.7845
Step 2: Find the equivalent value of mantissa using the Antilog table. Look for the row number that corresponds to 0.78 in the Antilog table. Select column number 4. Let's say you find the value 6081 in this row and column.
Step 3: Proceed to the mean difference column. Use the 0.78 row again and get the appropriate value in column 5. Let's say the value in this case is 7.
Step 4: Add the values discovered in steps 2 and 3. Add 6081 and 7: 6081 + 7 = 608.8.
Step 5: Insert the decimal point. You must multiply the characteristic value by 1. You now have 3. Then, after 3 digits, add the decimal point to obtain 608.8.
Result: The Antilogarithm of 2.7845 is approximately 608.8.
Example 2: Use the antilog formula and a calculator to check the answers in Example 1.
Solution:
By Antilog formula, antilog(x) = 10x
Antilog(2.7845) = 102.7845 = 608.8
A calculator is used to verify the answers.
Example 3: Calculate antilog(4.4771).
Solution:
By Antilog formula, antilog(x) = 10x
antilog(4.4771) = 104.4771
antilog(4.4771) ≈ 26645.82
So, Antilog(4.4771) is approximately equal to 26645.82.
Similar Reads
Logarithm In mathematics, a logarithm is the inverse operation of exponentiation. It is defined as the power to which the base number must be raised to get the given number.Logarithms serve as mathematical tools that help simplify complex calculations involving exponential relationships. If you know that bx =
3 min read
Laws of Logarithms The logarithm is the exponent or power to which a base is raised to get a particular number. For example, 'a' is the logarithm of 'm' to the base of 'x' if xm = a, then we can write it as m = logxa. Logarithms are invented to speed up the calculations and time will be reduced when we are multiplying
4 min read
Log Rules Logarithm rules are used to simplify and work with logarithmic expressions. They help relate logarithms to exponents and make complex calculations easier.A logarithm is the inverse of an exponent. It answers the question: "To what power must a base be raised to get a certain number?"Out of all these
7 min read
Logarithm Formula Logarithm is defined as the power to which a number is raised to yield some other values. Logarithms are the inverse of exponents. There is a unique way of reading the logarithm expression. For example, bx = n is called as 'x is the logarithm of n to the base b.There are two parts of the logarithm:
6 min read
Continuity and Differentiability of Logarithmic Function The word continuity means something which is continuous in nature. The flow of water is continuous, time in real life is continuous, and many more instances show the continuity in real life. In mathematics, the Continuous function is the one which when drawn on a graph does not show any breaks and i
5 min read
Derivative of Logarithmic Functions Derivative or Differentiation of Logarithmic Function as the name suggests, explores the derivatives of log functions with respect to some variable. As we know, derivatives are the backbone of Calculus and help us solve various real-life problems. Derivatives of the log functions are used to solve v
10 min read
Logarithmic Differentiation Method of finding a function's derivative by first taking the logarithm and then differentiating is called logarithmic differentiation. This method is specially used when the function is type y = f(x)g(x). In this type of problem where y is a composite function, we first need to take a logarithm, ma
8 min read
Log Table A Log Table in math is a reference tool to ease computations using logarithmic functions. It usually provides pre-computed logarithm values for various integers, commonly in a base like 10 or the natural logarithm base (e.g., ≈ 2.71828). Log tables allow users to obtain the logarithm of a given numb
9 min read
Antilog Table Antilog Table in math is a refrence tool used to reverse logarithmic computation and retrieve the original number from its logarithmic value.It typically provides a pre-computed antilogarithm value for various logarithmic inputs, commonly in base 1o or natural logarithm base( e.g ≅ 2.71828)Antilog t
7 min read
Change of Base in Logarithim The change of base formula is a useful concept in mathematics. That allows you to convert a logarithm from one base to another. Change of base formula in logarithm allows us to rewrite a logarithm with a different base. It allows us to compute logarithms using calculators or computational tools that
4 min read
Difference Between Log and Ln Logarithms(log) and natural logarithms(ln) are fundamental mathematical concepts that simplify complex calculations involving exponential relationships Logarithms are essential for solving equations where an unknown variable appears as the exponent of some other quantity. A logarithm can have any po
3 min read