Latent Dirichlet Allocation

Last Updated : 06 Jun, 2021

Topic Modeling:

Topic modeling is a way of abstract modeling to discover the abstract 'topics' that occur in the collections of documents. The idea is that we will perform unsupervised classification on different documents, which find some natural groups in topics. We can answer the following question using topic modeling.

What is the topic/main idea of the document?
Given a document, can we find another document with a similar topic?
How do topics field change over time?

Topic modeling can help in optimizing the search process. In this article, we will be discussing Latent Dirichlet Allocation, a topic modeling process.

Latent Dirichlet Allocation

Latent Dirichlet allocation is one of the most popular methods for performing topic modeling. Each document consists of various words and each topic can be associated with some words. The aim behind the LDA to find topics that the document belongs to, on the basis of words contains in it. It assumes that documents with similar topics will use a similar group of words. This enables the documents to map the probability distribution over latent topics and topics are probability distribution.

Setting up Generative Model:

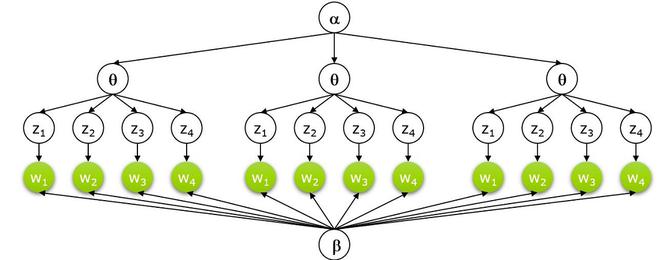
Let's suppose we have D documents using the vocabulary of V-word types. Each document consists of an N-words token (can be removed or padded ). Now, we assume K topics, this required a K-dimensional vector that represents the topic distribution for the document.
Each topic has a V-dimensional multinomial beta_k over words with a common symmetric prior.
For each topic 1...k:
- Draw a multinomial over words \varphi \sim Dir(\beta) .
For each document 1...d:
- Draw a multinomial over topics \theta \sim Dir(\alpha)
- For each word w_{N_d} :
  - Draw a topic Z_{N_d} \sim Mult(\theta_D) with Z_{N_d} \epsilon [1..K]
  - Draw a word W_{N_d} \sim Mult(\varphi).

Graphical Model of LDA:

P(W,Z,\theta,\varphi, \alpha, \beta) = \prod_{j=1}^{M} P(\theta_j ; \alpha) \prod_{i=1}^{K} P(\varphi_i ; \beta) \prod_{t=1}^{N} P(Z_{j,t} | \theta_j) P(W_{j,t} | \varphi_{Z_{j,t}})

D: \, Number \, of \, Documents \\ N_d: \, Number \, of \, words \, in \, a \, given \, document \\ \beta: \, dirichlet \, prior \, on \, the\, per-document \, topic\, distribution\\ \alpha: \, dirichlet \, prior \, on \, the\, per-topic \, word\, distribution\\ \theta_i : \, topic \, distribution \, for \, document \, i \\ \varphi_k: \, word \, distribution \, for \, topic \, k \\ z_{ij}: \, topic \, for \, the \, j-th \, word \, in \, document \, i \\ w_{ij}: \, specific \, word.

In the above equation, the LHS represents the probability of generating the original document from the LDA machine.
On the right side of the equation, there are 4 probability terms, the first two terms represent Dirichlet distribution and the other two represent the multinomial distribution. The first and third terms represent the distribution of topics but the second and fourth represent the word distribution. We will discuss the Dirichlet distribution first.

Dirichlet Distribution

Dirichlet's distribution can be defined as a probability density for a vector-valued input having the same characteristics as our multinomial parameter \theta . It has non-zero values such that:

x_1, x_2, ....,x_k \\ where \, x_i \, \epsilon \, (0,1) \, \, \sum_{i=1}^{K}x_i =1

Dir(\theta| \alpha) = \frac{1}{Beta(\alpha)}\prod_{i=1}^{K} \theta_i^{\alpha_i -1} \\ ; where Beta(\alpha) = \frac{\prod_{i=1}^{K} \Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^{K}\alpha_i)} where \alpha =(\alpha_1, \alpha_2,...\alpha_k )

The Dirichlet distribution is parameterized by the vector α, which has the same number of elements K as the multinomial parameter θ.
We can interpret p(θ|α) as answering the question "what is the probability density associated with multinomial distribution θ, given that our Dirichlet distribution has parameter α?".

Above is the visualization of the Dirichlet distribution, for our purpose, we can assume that corners/vertices represent the topics with words inside the triangle (the word is closer to the topic if it frequently relates with it. ) or vice-versa.
This distribution can be extended to more than 3-dimensions. For 4-dimension we can use tetrahedron and for further dimension. We can use k-1 dimensions simplex.

Inference:

The inference problem in LDA to compute the posterior of the hidden variables given the document and corpus parameter \alpha and \beta. That is to compute the P(

Example:

Let's consider we have two categories of topics, we have a word vector for each topic consisting of some words. Following are the words that represented different topics:

words	P(words \| topic =1)	P(words \| topic =2)
Heart	0.2	0
Love	0.2	0
Soul	0.2	0
Tears	0.2	0
Joy	0.2	0
Scientific	0	0.2
Knowledge	0	0.2
Work	0	0.2
Research	0	0.2
Mathematics	0	0.2

Now, we have some document, and we scan some documents for these words:

Words in Document	{P(topic=1), P(topic=2)}
MATHEMATICS KNOWLEDGE RESEARCH WORK MATHEMATICS RESEARCH WORK SCIENTIFIC MATHEMATICS WORK	{1,0}
SCIENTIFIC KNOWLEDGE MATHEMATICS SCIENTIFIC HEART LOVE TEARS KNOWLEDGE HEART	{0.25, 0.75}
MATHEMATICS HEART RESEARCH LOVE MATHEMATICS WORK TEARS SOUL KNOWLEDGE HEART	{0.5, 0.5}
WORK JOY SOUL TEARS MATHEMATICS TEARS LOVE LOVE LOVE SOUL	{0.75, 0.25}
TEARS LOVE JOY SOUL LOVE TEARS SOUL SOUL TEARS JOY	{1,0}

Now, we update the above words to topics matrix using the probabilities from document matrix below.

Implementation

In this implementation, we use scikit-learn and pyLDAvis. For datasets, we use yelp reviews datasets that can be found on the Yelp website.

Python3

# install pyldavis !pip install pyldavis # imports !pip install gensim pyLDAvis ! python3 -m spacy download en_core_web_sm  import pandas as pd import numpy as np  import string import spacy import nltk  import gensim from gensim import corpora  import matplotlib.pyplot as plt  import pyLDAvis import pyLDAvis.gensim_models  nltk.download('wordnet') from nltk.corpus import wordnet as wn nltk.download('stopwords') from nltk.corpus import stopwords import spacy.cli spacy.cli.download("en_core_web_md") import en_core_web_md # fetch yelp review dataset and clean it yelp_review = pd.read_csv('/content/yelp.csv') yelp_review.head() # print number of document and topics print(len(yelp_review)) print("Unique Business") print(len(yelp_review.groupby('business_id'))) print("Unique User") print(len(yelp_review.groupby('user_id')))  # clean the document and remove punctuation def clean_text(text):   delete_dict = {sp_char: '' for sp_char in string.punctuation}   delete_dict[' '] =' '   table = str.maketrans(delete_dict)   text1 = text.translate(table)   textArr= text1.split()   text2 = ' '.join([w for w in textArr if ( not w.isdigit() and                                             ( not w.isdigit() and len(w)>3))])    return text2.lower()    yelp_review['text'] = yelp_review['text'].apply(clean_text) yelp_review['Num_words_text'] = yelp_review['text'].apply(lambda x:len(str(x).split()))   print('-------Reviews By Stars --------') print(yelp_review['stars'].value_counts()) print(len(yelp_review)) print('-------------------------') max_review_data_sentence_length  = yelp_review['Num_words_text'].max()  # print short review ( mask = (yelp_review['Num_words_text'] < 100) & (yelp_review['Num_words_text'] >=20) df_short_reviews = yelp_review[mask] df_sampled = df_short_reviews.groupby('stars')     .apply(lambda x: x.sample(n=100)).reset_index(drop = True)  print('No of Short reviews') print(len(df_short_reviews))  # function to remove stopwords def remove_stopwords(text):     textArr = text.split(' ')     rem_text = " ".join([i for i in textArr if i not in stop_words])     return rem_text  # remove stopwords from the text stop_words = stopwords.words('english') df_sampled['text']=df_sampled['text'].apply(remove_stopwords)  # perform Lemmatization lp = en_core_web_md.load(disable=['parser', 'ner']) def lemmatization(texts,allowed_postags=['NOUN', 'ADJ']):         output = []        for sent in texts:              doc = nlp(sent)               output.append([token.lemma_                              for token in doc if token.pos_ in allowed_postags ])       return output text_list=df_sampled['text'].tolist() print(text_list[2]) tokenized_reviews = lemmatization(text_list) print(tokenized_reviews[2])  # convert to document term frequency: dictionary = corpora.Dictionary(tokenized_reviews) doc_term_matrix = [dictionary.doc2bow(rev) for rev in tokenized_reviews]  # Creating the object for LDA model using gensim library LDA = gensim.models.ldamodel.LdaModel  # Build LDA model lda_model = LDA(corpus=doc_term_matrix, id2word=dictionary,                  num_topics=10, random_state=100,                 chunksize=1000, passes=50,iterations=100) # print lda topics with respect to each word of document lda_model.print_topics()  # calculate perplexity and coherence print('\Perplexity: ', lda_model.log_perplexity(doc_term_matrix,                                                 total_docs=10000))    # calculate coherence coherence_model_lda = CoherenceModel(model=lda_model,                                      texts=tokenized_reviews, dictionary=dictionary ,                                       coherence='c_v') coherence_lda = coherence_model_lda.get_coherence() print('Coherence: ', coherence_lda)  # Now, we use pyLDA vis to visualize it pyLDAvis.sklearn.prepare(lda_tf, dtm_tf, tf_vectorizer)

Total reviews 10000 Unique Business 4174 Unique User 6403 -------------- -------Reviews by stars -------- 4    3526 5    3337 3    1461 2     927 1     749 Name: stars, dtype: int64 10000 ------------------------- No of Short reviews 6276 ------------------------- # review and tokenized version decided completely write place three times tried closed website posted hours open wants drive suburbs  youd better call first place cannot trusted wasted time spent hungry minutes walking disappointed vitamin  fail said  ['place', 'time', 'closed', 'website', 'hour', 'open', 'drive', 'suburb', 'first', 'place', 'time', 'hungry',  'minute', 'vitamin'] --------------------------- # LDA print topics [(0,   '0.015*"food" + 0.013*"good" + 0.010*"gelato" + 0.008*"sandwich" + 0.008*"chocolate" + 0.005*"wife" + 0.005*"next" + 0.005*"bad" + 0.005*"night" + 0.005*"sauce"'),  (1,   '0.030*"food" + 0.021*"great" + 0.019*"place" + 0.019*"good" + 0.016*"service" + 0.011*"time" + 0.011*"nice" + 0.008*"lunch" + 0.008*"dish" + 0.007*"staff"'),  (2,   '0.023*"food" + 0.023*"good" + 0.018*"place" + 0.014*"great" + 0.009*"star" + 0.009*"service" + 0.008*"store" + 0.007*"salad" + 0.007*"well" + 0.006*"pizza"'),  (3,   '0.035*"good" + 0.025*"place" + 0.023*"food" + 0.020*"time" + 0.015*"service" + 0.012*"great" + 0.009*"friend" + 0.008*"table" + 0.008*"chicken" + 0.007*"hour"'),  (4,   '0.020*"food" + 0.019*"time" + 0.012*"good" + 0.009*"restaurant" + 0.009*"great" + 0.008*"service" + 0.007*"order" + 0.006*"small" + 0.006*"hour" + 0.006*"next"'),  (5,   '0.012*"drink" + 0.009*"star" + 0.006*"worth" + 0.006*"place" + 0.006*"friend" + 0.005*"great" + 0.005*"kid" + 0.005*"drive" + 0.005*"simple" + 0.005*"experience"'),  (6,   '0.024*"place" + 0.015*"time" + 0.012*"food" + 0.011*"price" + 0.009*"good" + 0.009*"great" + 0.009*"kid" + 0.008*"staff" + 0.008*"nice" + 0.007*"happy"'),  (7,   '0.028*"place" + 0.019*"service" + 0.015*"good" + 0.014*"pizza" + 0.014*"time" + 0.013*"food" + 0.013*"great" + 0.011*"well" + 0.009*"order" + 0.007*"price"'),  (8,   '0.032*"food" + 0.026*"good" + 0.026*"place" + 0.015*"great" + 0.009*"service" + 0.008*"time" + 0.006*"price" + 0.006*"meal" + 0.006*"shop" + 0.006*"coffee"'),  (9,   '0.020*"food" + 0.014*"place" + 0.011*"meat" + 0.010*"line" + 0.009*"good" + 0.009*"minute" + 0.008*"time" + 0.008*"chicken" + 0.008*"wing" + 0.007*"hour"')] ------------------------------

Latent Dirichlet Allocation

pawangfg

Improve

Article Tags :

Practice Tags :

Latent Dirichlet Allocation

Topic Modeling:

Latent Dirichlet Allocation

Setting up Generative Model:

Graphical Model of LDA:

Inference:

Example:

Implementation

Similar Reads

Linear Model Regression

Linear Model Classification

Regularization

K-Nearest Neighbors (KNN)

Support Vector Machines

Decision Tree

Ensemble Learning