Lorentz Force - Definition, Formula, Examples
Last Updated : 21 May, 2024
Lorentz Force is the sum of Magnetic and Electrical Force experienced by a charge. When charges are moving under the influence of a magnetic field. They experience forces on them which cause them to sometimes change their direction, or if they are not able to do that. The forces of these individual charges become a force on the conductor carrying them. There are a lot of applications of this particular phenomenon in real life. All the motors that are employed in many devices around us work on this principle. To understand the working of these devices, it becomes essential to understand this concept. Let's look at this concept in detail.
What is Lorentz Force?
Lorentz force is the combination of the magnetic and electric forces created by an electromagnetic field. The Lorentz force is a fundamental notion in electromagnetism that describes the force experienced by a charged particle moving through an electromagnetic field. This force, named after the Dutch physicist Hendrik Lorentz, is critical to understanding the behavior of charged particles in a variety of physical situations, ranging from fundamental physics to practical technological applications.
Lorentz Force Formula
Let's say there is a point charge "q" which is moving with the velocity "v" and located at "r" at a time "t" in the presence of both electric field E(r) and magnetic field B(r). Both of these fields apply some force on the charge under their influence. The force on the charge due to their influence was first given by H.A Lorentz. The formula for this force was derived by Lorentz on the basis of rigorous experimentation that was done by Ampere and others.
The force on an electric charge "q" due to both of these fields is given by,
F = q [E(r) + v × B(r)]
F = Felec + Fmag
This force is called Lorentz Force.
Lorentz Force Formula for Continuous Charge Distribution
The Lorentz force law for a continuous charge distribution illustrates how an electric and magnetic field affects a charge distribution that is dispersed across space rather than concentrated at discrete spots.
dF = ρ(r)[E(r) + v(r) × B(r)] dv
where,
- ρ(r) is charge density at position r
- v(r) is velocity
- E(r) is electric field
- B(r) is Magnetic Field
Lorentz Force Formula on a Current-Carrying Wire
The force F on a straight segment of wire of length L, carrying a current I, in the presence of a magnetic field B, is given by:
F = I(L × B)
where,
- I is the electric current flowing through the wire
- L represents the length and direction of the wire segment in which the current flows
- B is magnetic field vector, indicating the strength and direction of the magnetic field at the location of the wire.
Relation between Magnetic Field and Lorentz Force
Looking at the formula, the relation between the electric field and the force which charges experience under its influence is known. In case of force experienced under the influence of the magnetic field, the following observations are made:
- It depends on q, v, and B (charge, velocity of the particle, and magnetic field). In the case of a negative charge, the direction of the force is reversed.
- There is a vector product between the velocity and magnetic field. The direction of force is perpendicular to both of the quantities. In case, velocity and magnetic field become parallel. The force on the charge becomes zero.
- Magnetic force on any charge is zero if it's not moving that is |v| = 0.

The above figure shows the direction of the magnetic force acting on the particle. The force on the positively charged particle with velocity "v" and making an angle θ with the direction of the magnetic field is given by the right-hand rule.
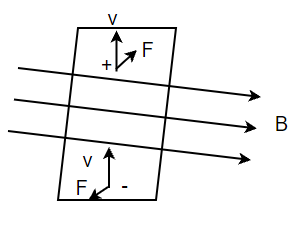
It shows a moving charged particle that is deflected from its path due to a magnetic field. Notice that both of the charges get deflected in different directions.
Lorentz Force and Right Hand Rule
The direction of the force F can be determined using the right-hand rule:
- Point your fingers in the direction of the current (L).
- Curl your fingers toward the direction of the magnetic field (B).
- Your thumb will point in the direction of the force F on the wire.
Importance of Lorentz Force in Physics
Unification of Electric and Magnetic Fields:
- The Lorentz force is central to Maxwell's equations, which describe how electric and magnetic fields propagate and interact with matter.
- It highlights the interconnected nature of electricity and magnetism.
Foundation of Electrodynamics:
- Understanding the Lorentz force is crucial for studying the behavior of charged particles in fields, which is essential in both classical and modern physics, including quantum mechanics and relativity.
Application of Lorentz Force
The application of Lorentz Force are mentioned below:
Cathode Ray Tube (CRT): Used in old televisions and oscilloscopes. The Lorentz force is utilized to direct electron paths, resulting in images on the screen.
Mass Spectrometry: Separates ions according to their mass-to-charge ratio. The Lorentz force deflects ions in a magnetic field, allowing their mass to be determined.
Cyclotrons and synchrotrons: The Lorentz force bends the path of charged particles, allowing them to accelerate at high speeds in circular or spiral routes.
Hall Effect Sensors: It Measure magnetic fields. The Lorentz force creates a voltage difference across a conductor, which can be used to calculate the magnetic field intensity.
Electromagnetic induction: It is Fundamental to the operation of electric generators and transformers. The motion of conductors in magnetic fields induces an electromotive force due to the Lorentz force acting on the charge carriers.
Also, Check
Solved Examples on Lorentz Force
Example 1: Find out the magnitude of the force experienced when the unit charge is kept under the influence of 5 N/C electric fields.
Solution:
The for on the charge is given by,
F = qE
⇒ F = (1)(5)
⇒ F = 5 N/s.
Example 2: Find out the magnitude of the force experienced when a 5C charge is kept under the influence of 25 N/C electric fields.
Solution:
The for on the charge is given by,
F = qE
⇒ F = (5)(25)
⇒ F = 125 N/s.
Example 3: Find out the magnitude of the force experienced when a 5C charge is moving at 10m/s under the influence of a 25 N/C electric field. The magnetic field of 10 magnitudes is perpendicular to the direction of the electric field and velocity. Find out the magnitude of the force experienced by the charge.
Solution:
The for on the charge is given by,
F = qE + q(v × B)
⇒ F = (5)(25) + 5 (10 × 10 × sin(90))
⇒ F = 125 + 5(100)
⇒ F = 125 + 500
⇒ F = 625 N
Example 4: Find out the magnitude of the force experienced when a 10C charge is moving at 10m/s under the influence of 5 N/C electric fields. The magnetic field of 5 magnitudes is perpendicular to the direction of the electric field and velocity. Find out the magnitude of the force experienced by the charge.
Solution:
The for on the charge is given by,
F = qE + q(v × B)
⇒ F = (10)(5) + 10 (10 × 5 × sin(90))
⇒ F = 50 + 500
⇒ F = 550 N
Example 5: Find out the magnitude of the force experienced when a -2C charge is moving at 10m/s under the influence of 5 N/C electric fields. The magnetic field of 5 magnitudes is 30° to the direction of the electric field and velocity. Find out the magnitude of the force experienced by the charge.
Solution:
The for on the charge is given by,
F = qE + q(v × B)
⇒ F = (-2)(5) + (-2) (10 × 5 × sin(30))
⇒ F = -10 + -100 × 0.5
⇒ F = -60 N
Similar Reads
Linear Momentum - Definition, Formula, Examples Linear Momentum is the physical property of a mass moving with a certain velocity in a straight line path. Linear momentum is given as the product of the mass of the object and the velocity with which it is moving. In the physical world, we can realize the significance of linear momentum from the fa
7 min read
Conservative Forces - Definition, Formula, Examples Conservative Force is a type of force which is independent of path taken to do a work. This means when an when force applied in moving an object from one position to another is the same irrespective of the path taken, it is called conservative force. A force is a push or pull acting on an object. In
7 min read
Centripetal Force Formula with Examples Centripetal force is a force that operates on a body traveling in a circular direction and is directed toward the center around which the body is moving. When an item moves at a constant speed around a circular route, it encounters an accelerating centripetal force toward the center.Table of Content
8 min read
What is Magnetic Force? Definition, Formula, Applications, and Examples Magnetic force is an invisible force that draws in or pushes away objects, similar to how magnets pull metals like iron. This occurs because of the magnetic characteristics of tiny particles within materials.Magnets have two poles, North and South, that either attract or repel depending on their ali
13 min read
Magnitude of a Vector: Definition | Formula | Solved Examples Vector quantities are physical quantities that have both direction and magnitude, like displacement, velocity, force, etc.The direction represents the way in which the vector is pointing.The magnitude of a vector represents its length and is always a positive scalar value.For any vector \overrightar
6 min read