Level of Each node in a Tree from source node (using BFS)
Last Updated : 01 Aug, 2022
Given a tree with v vertices, find the level of each node in a tree from the source node.
Examples:
Input :
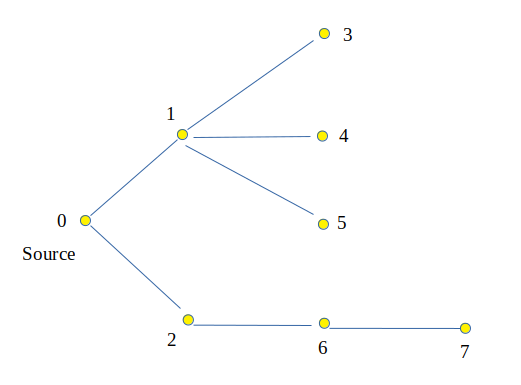
Output : Node Level 0 0 1 1 2 1 3 2 4 2 5 2 6 2 7 3 Explanation :
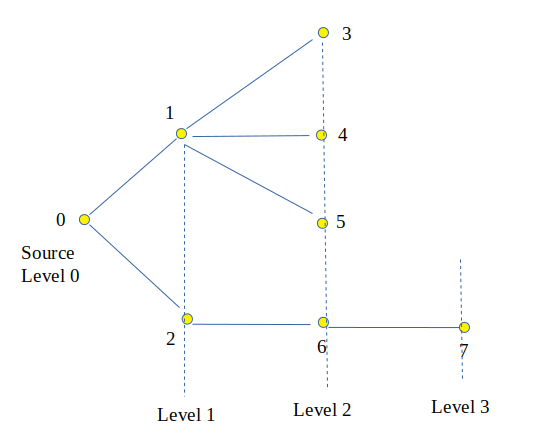
Input:
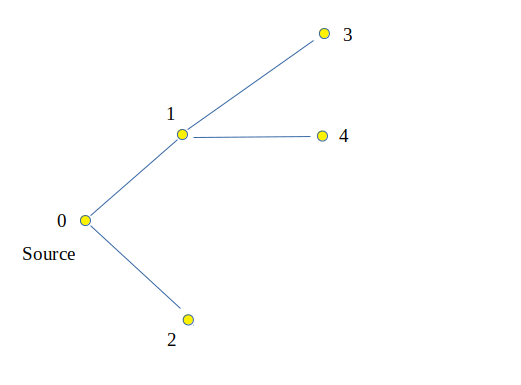
Output : Node Level 0 0 1 1 2 1 3 2 4 2 Explanation:
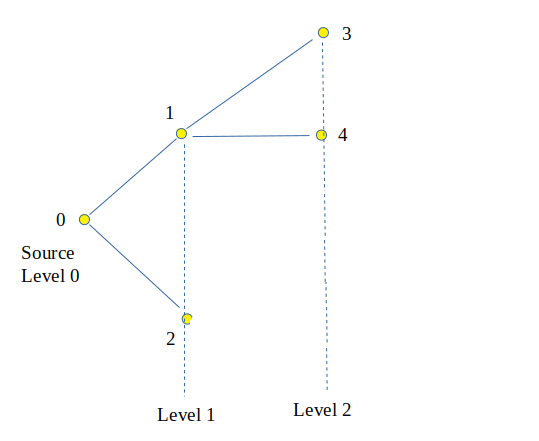
Approach:
BFS(Breadth-First Search) is a graph traversal technique where a node and its neighbours are visited first and then the neighbours of neighbours. In simple terms, it traverses level-wise from the source. First, it traverses level 1 nodes (direct neighbours of source node) and then level 2 nodes (neighbours of source node) and so on. The BFS can be used to determine the level of each node from a given source node.
Algorithm:
- Create the tree, a queue to store the nodes and insert the root or starting node in the queue. Create an extra array level of size v (number of vertices) and create a visited array.
- Run a loop while size of queue is greater than 0.
- Mark the current node as visited.
- Pop one node from the queue and insert its childrens (if present) and update the size of the inserted node as level[child] = level[node] + 1.
- Print all the node and its level.
Implementation:
C++ // CPP Program to determine level of each node // and print level #include <bits/stdc++.h> using namespace std; // function to determine level of each node starting // from x using BFS void printLevels(vector<int> graph[], int V, int x) { // array to store level of each node int level[V]; bool marked[V]; // create a queue queue<int> que; // enqueue element x que.push(x); // initialize level of source node to 0 level[x] = 0; // marked it as visited marked[x] = true; // do until queue is empty while (!que.empty()) { // get the first element of queue x = que.front(); // dequeue element que.pop(); // traverse neighbors of node x for (int i = 0; i < graph[x].size(); i++) { // b is neighbor of node x int b = graph[x][i]; // if b is not marked already if (!marked[b]) { // enqueue b in queue que.push(b); // level of b is level of x + 1 level[b] = level[x] + 1; // mark b marked[b] = true; } } } // display all nodes and their levels cout << "Nodes" << " " << "Level" << endl; for (int i = 0; i < V; i++) cout << " " << i << " --> " << level[i] << endl; } // Driver Code int main() { // adjacency graph for tree int V = 8; vector<int> graph[V]; graph[0].push_back(1); graph[0].push_back(2); graph[1].push_back(3); graph[1].push_back(4); graph[1].push_back(5); graph[2].push_back(5); graph[2].push_back(6); graph[6].push_back(7); // call levels function with source as 0 printLevels(graph, V, 0); return 0; } // Java Program to determine level of each node // and print level import java.util.*; class GFG { // function to determine level of each node starting // from x using BFS static void printLevels(Vector<Vector<Integer> > graph, int V, int x) { // array to store level of each node int level[] = new int[V]; boolean marked[] = new boolean[V]; // create a queue Queue<Integer> que = new LinkedList<Integer>(); // enqueue element x que.add(x); // initialize level of source node to 0 level[x] = 0; // marked it as visited marked[x] = true; // do until queue is empty while (que.size() > 0) { // get the first element of queue x = que.peek(); // dequeue element que.remove(); // traverse neighbors of node x for (int i = 0; i < graph.get(x).size(); i++) { // b is neighbor of node x int b = graph.get(x).get(i); // if b is not marked already if (!marked[b]) { // enqueue b in queue que.add(b); // level of b is level of x + 1 level[b] = level[x] + 1; // mark b marked[b] = true; } } } // display all nodes and their levels System.out.println("Nodes" + " " + "Level"); for (int i = 0; i < V; i++) System.out.println(" " + i + " --> " + level[i]); } // Driver Code public static void main(String args[]) { // adjacency graph for tree int V = 8; Vector<Vector<Integer> > graph = new Vector<Vector<Integer> >(); for (int i = 0; i < V + 1; i++) graph.add(new Vector<Integer>()); graph.get(0).add(1); graph.get(0).add(2); graph.get(1).add(3); graph.get(1).add(4); graph.get(1).add(5); graph.get(2).add(5); graph.get(2).add(6); graph.get(6).add(7); // call levels function with source as 0 printLevels(graph, V, 0); } } // This code is contributed by Arnab Kundu # Python3 Program to determine level # of each node and print level import queue # function to determine level of # each node starting from x using BFS def printLevels(graph, V, x): # array to store level of each node level = [None] * V marked = [False] * V # create a queue que = queue.Queue() # enqueue element x que.put(x) # initialize level of source # node to 0 level[x] = 0 # marked it as visited marked[x] = True # do until queue is empty while (not que.empty()): # get the first element of queue x = que.get() # traverse neighbors of node x for i in range(len(graph[x])): # b is neighbor of node x b = graph[x][i] # if b is not marked already if (not marked[b]): # enqueue b in queue que.put(b) # level of b is level of x + 1 level[b] = level[x] + 1 # mark b marked[b] = True # display all nodes and their levels print("Nodes", " ", "Level") for i in range(V): print(" ", i, " --> ", level[i]) # Driver Code if __name__ == '__main__': # adjacency graph for tree V = 8 graph = [[] for i in range(V)] graph[0].append(1) graph[0].append(2) graph[1].append(3) graph[1].append(4) graph[1].append(5) graph[2].append(5) graph[2].append(6) graph[6].append(7) # call levels function with source as 0 printLevels(graph, V, 0) # This code is contributed by PranchalK // C# Program to determine level of each node // and print level using System; using System.Collections.Generic; class GFG { // function to determine level of each node starting // from x using BFS static void printLevels(List<List<int> > graph, int V, int x) { // array to store level of each node int[] level = new int[V]; Boolean[] marked = new Boolean[V]; // create a queue Queue<int> que = new Queue<int>(); // enqueue element x que.Enqueue(x); // initialize level of source node to 0 level[x] = 0; // marked it as visited marked[x] = true; // do until queue is empty while (que.Count > 0) { // get the first element of queue x = que.Peek(); // dequeue element que.Dequeue(); // traverse neighbors of node x for (int i = 0; i < graph[x].Count; i++) { // b is neighbor of node x int b = graph[x][i]; // if b is not marked already if (!marked[b]) { // enqueue b in queue que.Enqueue(b); // level of b is level of x + 1 level[b] = level[x] + 1; // mark b marked[b] = true; } } } // display all nodes and their levels Console.WriteLine("Nodes" + " " + "Level"); for (int i = 0; i < V; i++) Console.WriteLine(" " + i + " --> " + level[i]); } // Driver Code public static void Main(String[] args) { // adjacency graph for tree int V = 8; List<List<int> > graph = new List<List<int> >(); for (int i = 0; i < V + 1; i++) graph.Add(new List<int>()); graph[0].Add(1); graph[0].Add(2); graph[1].Add(3); graph[1].Add(4); graph[1].Add(5); graph[2].Add(5); graph[2].Add(6); graph[6].Add(7); // call levels function with source as 0 printLevels(graph, V, 0); } } // This code is contributed by Princi Singh <script> // Javascript Program to determine level of each node // and print level // function to determine level of each node starting // from x using BFS function printLevels(graph, V, x) { // array to store level of each node var level = Array(V); var marked = Array(V).fill(false); // create a queue var que = []; // enqueue element x que.push(x); // initialize level of source node to 0 level[x] = 0; // marked it as visited marked[x] = true; // do until queue is empty while (que.length > 0) { // get the first element of queue x = que[0]; // dequeue element que.shift(); // traverse neighbors of node x for (var i = 0; i < graph[x].length; i++) { // b is neighbor of node x var b = graph[x][i]; // if b is not marked already if (!marked[b]) { // enqueue b in queue que.push(b); // level of b is level of x + 1 level[b] = level[x] + 1; // mark b marked[b] = true; } } } // display all nodes and their levels document.write("Nodes" + " " + "Level<br>"); for (var i = 0; i < V; i++) document.write(" " + i +" --> " + level[i]+"<br>"); } // Driver Code // adjacency graph for tree var V = 8; var graph = Array.from(Array(V+1), ()=>Array()); graph[0].push(1); graph[0].push(2); graph[1].push(3); graph[1].push(4); graph[1].push(5); graph[2].push(5); graph[2].push(6); graph[6].push(7); // call levels function with source as 0 printLevels(graph, V, 0); // This code is contributed by importantly. </script> OutputNodes Level 0 --> 0 1 --> 1 2 --> 1 3 --> 2 4 --> 2 5 --> 2 6 --> 2 7 --> 3
Complexity Analysis:
- Time Complexity: O(n).
In BFS traversal every node is visited only once, so Time Complexity is O(n). - Space Complexity: O(n).
The space is required to store the nodes in a queue.