The trie data structure, also known as a prefix tree, is a tree-like data structure used for efficient retrieval of key-value pairs. It is commonly used for implementing dictionaries and autocomplete features, making it a fundamental component in many search algorithms. In this article, we will explore all about Trie data structures in detail.
Trie Data Structure
What is Trie Data Structure?
Trie data structure is defined as a Tree based data structure that is used for storing a collection of strings and performing efficient search, insert, delete, prefix search and sorted-traversal-of-all operations on them. The word Trie is derived from reTRIEval, which means finding something or obtaining it.
Trie data structure follows a property that If two strings have a common prefix then they will have the same ancestor in the trie. This particular property allows to find all words with a given prefix.
What is need of Trie Data Structure?
A Trie data structure is used for storing and retrieval of data and the same operations could be done using another data structure which is Hash Table but Trie data structure can perform these operations more efficiently than a Hash Table. Moreover, Trie has its own advantage over the Hash table. A Trie data structure can be used for prefix-based searching and a sorted traversal of all words. So a Trie has advantages of both hash table and self balancing binary search trees. However the main issue with Trie is extra memory space required to store words and the space may become huge for long list of words and/or for long words.
Advantages of Trie Data Structure over a Hash Table:
The A trie data structure has the following advantages over a hash table:
- We can efficiently do prefix search (or auto-complete) with Trie.
- We can easily print all words in alphabetical order which is not easily possible with hashing.
- There is no overhead of Hash functions in a Trie data structure.
- Searching for a String even in the large collection of strings in a Trie data structure can be done in O(L) Time complexity, Where L is the number of words in the query string. This searching time could be even less than O(L) if the query string does not exist in the trie.
Properties of a Trie Data Structure
Below are some important properties of the Trie data structure:
- Each Trie has an empty root node, with links (or references) to other nodes
- Each node of a Trie represents a string and each edge represents a character.
- Every node consists of hashmaps or an array of pointers, with each index representing a character and a flag to indicate if any string ends at the current node.
- Trie data structure can contain any number of characters including alphabets, numbers, and special characters. But for this article, we will discuss strings with characters a-z. Therefore, only 26 pointers need for every node, where the 0th index represents ‘a’ and the 25th index represents ‘z’ characters.
- Each path from the root to any node represents a word or string.
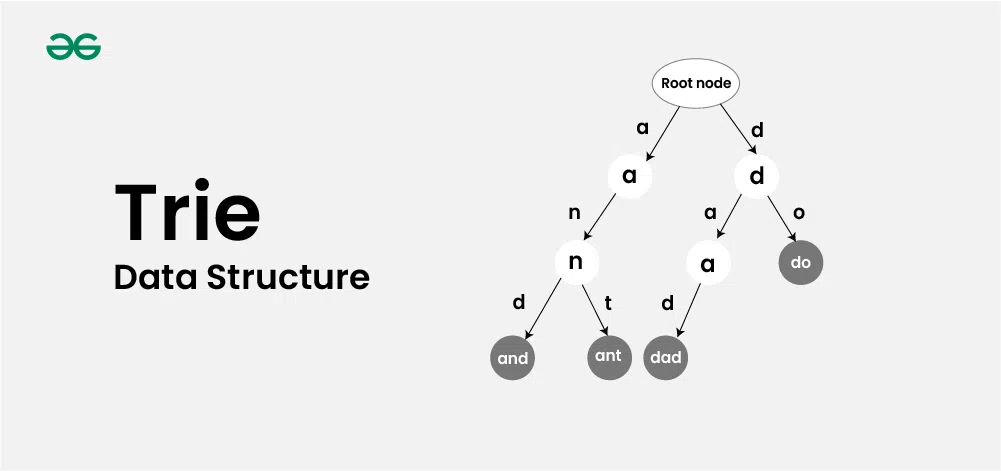
Below is a simple example of Trie data structure.
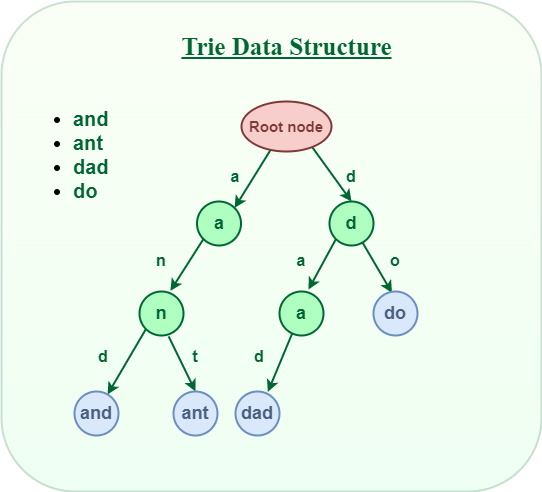
Trie Data Structure
How does Trie Data Structure work?
Trie data structure can contain any number of characters including alphabets, numbers, and special characters. But for this article, we will discuss strings with characters a-z. Therefore, only 26 pointers need for every node, where the 0th index represents ‘a’ and the 25th index represents ‘z’ characters.
Any lowercase English word can start with a-z, then the next letter of the word could be a-z, the third letter of the word again could be a-z, and so on. So for storing a word, we need to take an array (container) of size 26 and initially, all the characters are empty as there are no words and it will look as shown below.
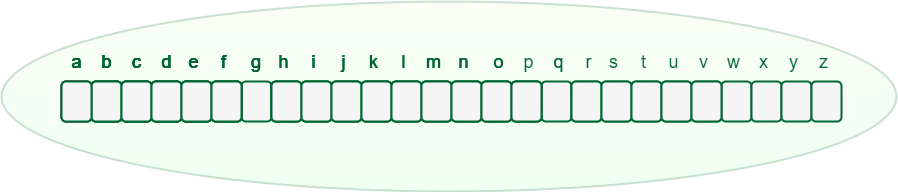
An array of pointers inside every Trie node
Let’s see how a word “and” and “ant” is stored in the Trie data structure:
- Store “and” in Trie data structure:
- The word “and” starts with “a“, So we will mark the position “a” as filled in the Trie node, which represents the use of “a”.
- After placing the first character, for the second character again there are 26 possibilities, So from “a“, again there is an array of size 26, for storing the 2nd character.
- The second character is “n“, So from “a“, we will move to “n” and mark “n” in the 2nd array as used.
- After “n“, the 3rd character is “d“, So mark the position “d” as used in the respective array.
- Store “ant” in the Trie data structure:
- The word “ant” starts with “a” and the position of “a” in the root node has already been filled. So, no need to fill it again, just move to the node ‘a‘ in Trie.
- For the second character ‘n‘ we can observe that the position of ‘n’ in the ‘a’ node has already been filled. So, no need to fill it again, just move to node ‘n’ in Trie.
- For the last character ‘t‘ of the word, The position for ‘t‘ in the ‘n‘ node is not filled. So, filled the position of ‘t‘ in ‘n‘ node and move to ‘t‘ node.
After storing the word “and” and “ant” the Trie will look like this:
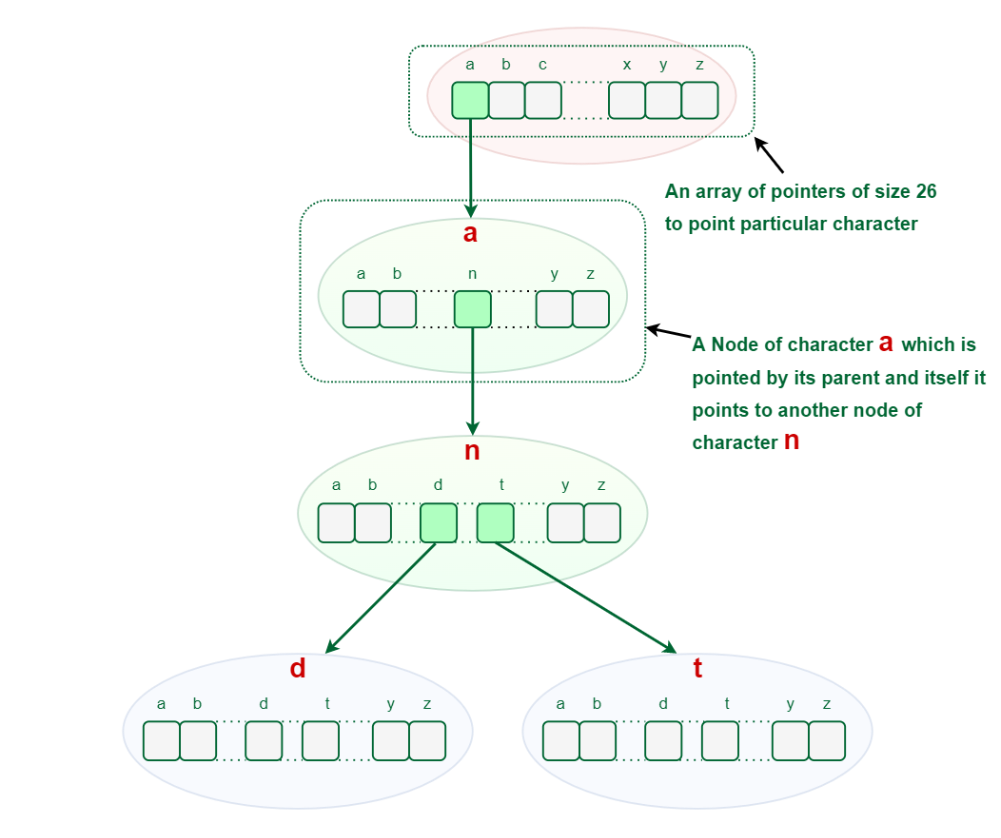
Representation of Trie Node:
Every Trie node consists of a character pointer array or hashmap and a flag to represent if the word is ending at that node or not. But if the words contain only lower-case letters (i.e. a-z), then we can define Trie Node with an array instead of a hashmap.
C++ struct TrieNode { struct TrieNode* children[ALPHABET_SIZE]; // This will keep track of number of strings that are // stored in the Trie from root node to any Trie node. int wordCount = 0; }; public class TrieNode { public TrieNode[] children; public int wordCount; public TrieNode() { children = new TrieNode[26]; // This will keep track of number of strings that // are stored in the Trie from root node to any Trie // node. wordCount = 0; } } # Python code class TrieNode: # Trie node class def _init_(self): self.children = [None for _ in range(26)] # This will keep track of number of strings that are # stored in the Trie from root node to any Trie node. self.wordCount = 0 # This code is contributed by ishankhandelwals.
// Include namespace system using System; public class TrieNode { public TrieNode[] children; public int wordCount; public TrieNode() { this.children = new TrieNode[26]; // This will keep track of number of strings that // are stored in the Trie from root node to any Trie // node. this.wordCount = 0; } } // JS code class TrieNode { constructor() { this.children = new Array(26); // This will keep track of number of strings that are // stored in the Trie from root node to any Trie node. this.wordCount = 0; } } // This code is contributed by ishankhandelwals. Basic Operations on Trie Data Structure:
- Insertion
- Search
- Deletion
1. Insertion in Trie Data Structure:
This operation is used to insert new strings into the Trie data structure. Let us see how this works:
Let us try to Insert “and” & “ant” in this Trie:
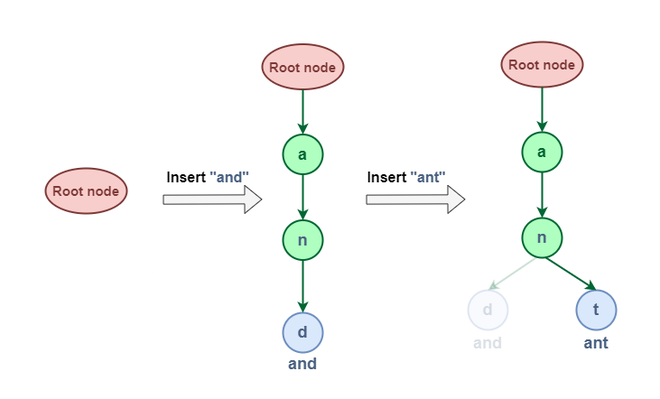
Insert “and” & “ant”
From the above representation of insertion, we can see that the word “and” & “ant” have shared some common node (i.e “an”) this is because of the property of the Trie data structure that If two strings have a common prefix then they will have the same ancestor in the trie.
Now let us try to Insert “dad” & “do”:
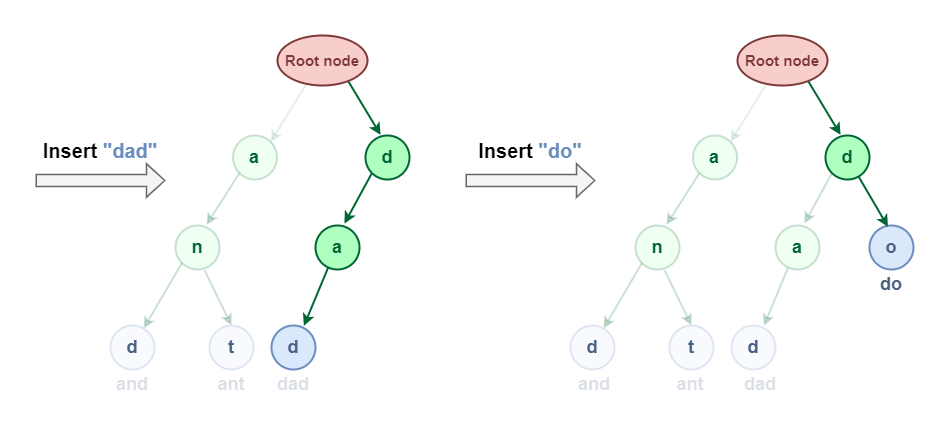
Insertion in Trie Data Structure
Implementation of Insertion in Trie data structure:
Algorithm:
- Define a function insert(TrieNode *root, string &word) which will take two parameters one for the root and the other for the string that we want to insert in the Trie data structure.
- Now take another pointer currentNode and initialize it with the root node.
- Iterate over the length of the given string and check if the value is NULL or not in the array of pointers at the current character of the string.
- If It’s NULL then, make a new node and point the current character to this newly created node.
- Move the curr to the newly created node.
- Finally, increment the wordCount of the last currentNode, this implies that there is a string ending currentNode.
Below is the implementation of the above algorithm:
C++ void insert_key(TrieNode* root, string& key) { // Initialize the currentNode pointer // with the root node TrieNode* currentNode = root; // Iterate across the length of the string for (auto c : key) { // Check if the node exist for the current // character in the Trie. if (currentNode->childNode[c - 'a'] == NULL) { // If node for current character does not exist // then make a new node TrieNode* newNode = new TrieNode(); // Keep the reference for the newly created // node. currentNode->childNode[c - 'a'] = newNode; } // Now, move the current node pointer to the newly // created node. currentNode = currentNode->childNode[c - 'a']; } // Increment the wordEndCount for the last currentNode // pointer this implies that there is a string ending at // currentNode. currentNode->wordCount++; } static void insert(TrieNode root, String key) { // Initialize the currentNode pointer with the root node TrieNode currentNode = root; for (int i = 0; i < key.length(); i++) { int index = key.charAt(i) - 'a'; // Check if the node exist for the current // character in the Trie. if (currentNode.childNode[index] == null) { // Keep the reference for the newly created // node. currentNode.childNode[index] = new TrieNode(); } // Now, move the current node pointer to the newly // created node. currentNode = currentNode.childNode[index]; } // Increment the wordEndCount for the last currentNode // pointer this implies that there is a string ending at // currentNode. currentNode.wordCount++; } def insert_key(root, key): # Initialize the currentNode pointer # with the root node currentNode = root # Iterate across the length of the string for c in key: # Check if the node exist for the current # character in the Trie. if currentNode.childNode[ord(c) - ord('a')] == None: # If node for current character does not exist # then make a new node newNode = TrieNode() # Keep the reference for the newly created # node. currentNode.childNode[ord(c) - ord('a')] = newNode # Now, move the current node pointer to the newly # created node. currentNode = currentNode.childNode[ord(c) - ord('a')] # Increment the wordEndCount for the last currentNode # pointer this implies that there is a string ending at # currentNode. currentNode.wordCount += 1 static void insert(TrieNode root, string key) { // Initialize the currentNode pointer with the root node TrieNode currentNode = root; for (int i = 0; i < key.Length; i++) { int index = key[i] - 'a'; // Check if the node exist for the current // character in the Trie. if (currentNode.childNode[index] == null) { // Keep the reference for the newly created // node. currentNode.childNode[index] = new TrieNode(); } // Now, move the current node pointer to the newly // created node. currentNode = currentNode.childNode[index]; } // Increment the wordEndCount for the last currentNode // pointer this implies that there is a string ending at // currentNode. currentNode.wordCount++; } // JS code for above approach function insert_key(root, key) { // Initialize the currentNode pointer // with the root node let currentNode = root; // Iterate across the length of the string for (let i=0;i<key.length;i++) { // Check if the node exist for the current // character in the Trie. if (currentNode.childNode[key[i]- 'a'] == NULL) { // If node for current character does not exist // then make a new node let newNode = new TrieNode(); // Keep the reference for the newly created // node. currentNode.childNode[key[i] - 'a'] = newNode; } // Now, move the current node pointer to the newly // created node. currentNode = currentNode.childNode[key[i] - 'a']; } // Increment the wordEndCount for the last currentNode // pointer this implies that there is a string ending at // currentNode. currentNode.wordCount++; } 2. Searching in Trie Data Structure:
Search operation in Trie is performed in a similar way as the insertion operation but the only difference is that whenever we find that the array of pointers in curr node does not point to the current character of the word then return false instead of creating a new node for that current character of the word.
This operation is used to search whether a string is present in the Trie data structure or not. There are two search approaches in the Trie data structure.
- Find whether the given word exists in Trie.
- Find whether any word that starts with the given prefix exists in Trie.
There is a similar search pattern in both approaches. The first step in searching a given word in Trie is to convert the word to characters and then compare every character with the trie node from the root node. If the current character is present in the node, move forward to its children. Repeat this process until all characters are found.
2.1 Searching Prefix in Trie Data Structure:
Search for the prefix “an” in the Trie Data Structure.
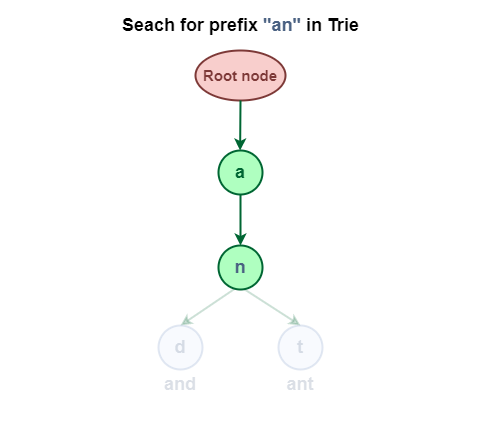
Search for the prefix “an” in Trie
Implementation of Prefix Search in Trie data structure:
C++ bool isPrefixExist(TrieNode* root, string& key) { // Initialize the currentNode pointer // with the root node TrieNode* currentNode = root; // Iterate across the length of the string for (auto c : key) { // Check if the node exist for the current // character in the Trie. if (currentNode->childNode[c - 'a'] == NULL) { // Given word as a prefix does not exist in Trie return false; } // Move the currentNode pointer to the already // existing node for current character. currentNode = currentNode->childNode[c - 'a']; } // Prefix exist in the Trie return true; } public boolean isPrefixExist(TrieNode root, String key) { // Initialize the currentNode pointer // with the root node TrieNode currentNode = root; // Iterate across the length of the string for (char c : key.toCharArray()) { // Check if the node exist for the current // character in the Trie. if (currentNode.childNode[c - 'a'] == null) { // Given word as a prefix does not exist in Trie return false; } // Move the currentNode pointer to the already // existing node for current character. currentNode = currentNode.childNode[c - 'a']; } // Prefix exist in the Trie return true; } def is_prefix_exist(root, key): # Initialize the currentNode pointer # with the root node current_node = root # Iterate across the length of the string for c in key: # Check if the node exist for the current # character in the Trie. if current_node.child_node[ord(c) - ord('a')] is None: # Given word as a prefix does not exist in Trie return False # Move the currentNode pointer to the already # existing node for current character. current_node = current_node.child_node[ord(c) - ord('a')] # Prefix exist in the Trie return True public bool isPrefixExist(TrieNode root, string key) { // Initialize the currentNode pointer // with the root node TrieNode currentNode = root; // Iterate across the length of the string foreach (char c in key) { // Check if the node exist for the current // character in the Trie. if (currentNode.childNode[c - 'a'] == null) { // Given word as a prefix does not exist in Trie return false; } // Move the currentNode pointer to the already // existing node for current character. currentNode = currentNode.childNode[c - 'a']; } // Prefix exist in the Trie return true; } function isPrefixExist(root, key) { // Initialize the currentNode pointer with the root node let currentNode = root; // Iterate across the length of the string for (let c of key) { // Check if the node exist for the current character in the Trie. if (currentNode.childNode[c.charCodeAt(0) - 'a'.charCodeAt(0)] === null) { // Given word as a prefix does not exist in Trie return false; } // Move the currentNode pointer to the already existing node for current character. currentNode = currentNode.childNode[c.charCodeAt(0) - 'a'.charCodeAt(0)]; } // Prefix exist in the Trie return true; } 2.2 Searching Complete word in Trie Data Structure:
It is similar to prefix search but additionally, we have to check if the word is ending at the last character of the word or not.
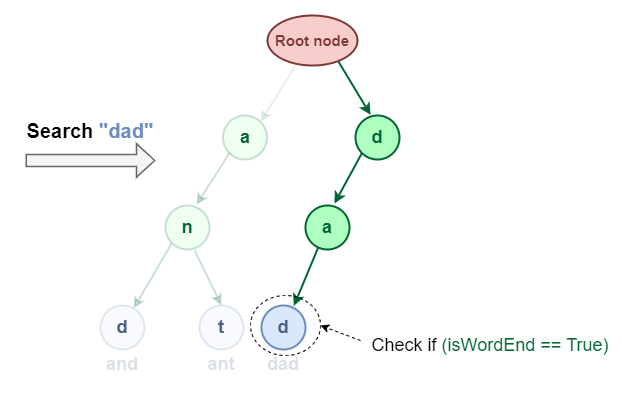
Search “dad” in the Trie data structure
Implementation of Search in Trie data structure:
C++ bool search_key(TrieNode* root, string& key) { // Initialize the currentNode pointer // with the root node TrieNode* currentNode = root; // Iterate across the length of the string for (auto c : key) { // Check if the node exist for the current // character in the Trie. if (currentNode->childNode[c - 'a'] == NULL) { // Given word does not exist in Trie return false; } // Move the currentNode pointer to the already // existing node for current character. currentNode = currentNode->childNode[c - 'a']; } return (currentNode->wordCount > 0); } // Returns true if key presents in trie, else false static boolean search(TrieNode root, String key) { // Initialize the currentNode // with the root node TrieNode currentNode = root; for (int i = 0; i < key.length(); i++) { int index = key.charAt(i) - 'a'; // Check if the node exist for the current // character in the Trie. if (currentNode.childNode[index] == null) return false; // Move the currentNode to the already // existing node for current character. currentNode = currentNode.childNode[index]; } return (currentNode.isEndOfWord); } def search_key(root, key): # Initialize the currentNode pointer with the root node currentNode = root # Iterate across the length of the string for c in key: # Check if the node exist for the current character in the Trie if currentNode.childNode[ord(c) - ord('a')] is None: # Given word does not exist in Trie return False # Move the currentNode pointer to the already existing node for current character currentNode = currentNode.childNode[ord(c) - ord('a')] # Return if the wordCount is greater than 0 return currentNode.wordCount > 0 public bool SearchKey(TrieNode root, string key) { // Initialize the currentNode pointer with the root node TrieNode currentNode = root; // Iterate across the length of the string foreach (char c in key) { // Check if the node exist for the current character in the Trie if (currentNode.childNode[c - 'a'] == null) { // Given word does not exist in Trie return false; } // Move the currentNode pointer to the already existing node for current character currentNode = currentNode.childNode[c - 'a']; } // Return if the wordCount is greater than 0 return currentNode.wordCount > 0; } //This code is contributed by shivamsharma215 function searchKey(root, key) { let currentNode = root; for (let c of key) { if (!currentNode.childNode[c.charCodeAt(0) - 'a'.charCodeAt(0)]) { return false; } currentNode = currentNode.childNode[c.charCodeAt(0) - 'a'.charCodeAt(0)]; } return currentNode.wordCount > 0; } 3. Deletion in Trie Data Structure
This operation is used to delete strings from the Trie data structure. There are three cases when deleting a word from Trie.
- The deleted word is a prefix of other words in Trie.
- The deleted word shares a common prefix with other words in Trie.
- The deleted word does not share any common prefix with other words in Trie.
3.1 The deleted word is a prefix of other words in Trie.
As shown in the following figure, the deleted word “an” share a complete prefix with another word “and” and “ant“.
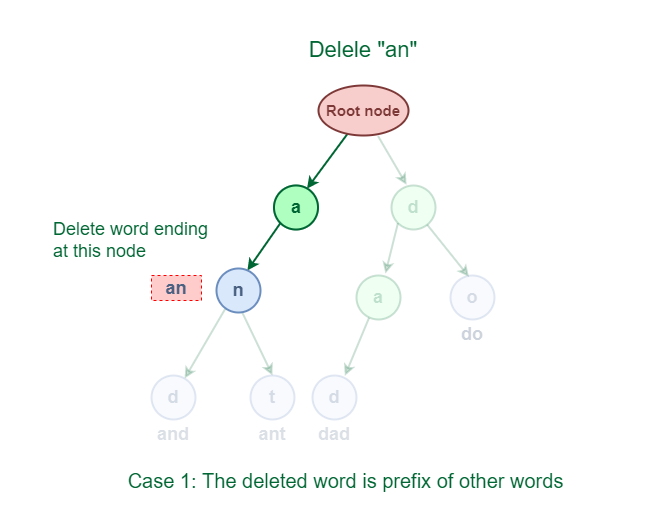
Deletion of word which is a prefix of other words in Trie
An easy solution to perform a delete operation for this case is to just decrement the wordCount by 1 at the ending node of the word.
3.2 The deleted word shares a common prefix with other words in Trie.
As shown in the following figure, the deleted word “and” has some common prefixes with other words ‘ant’. They share the prefix ‘an’.
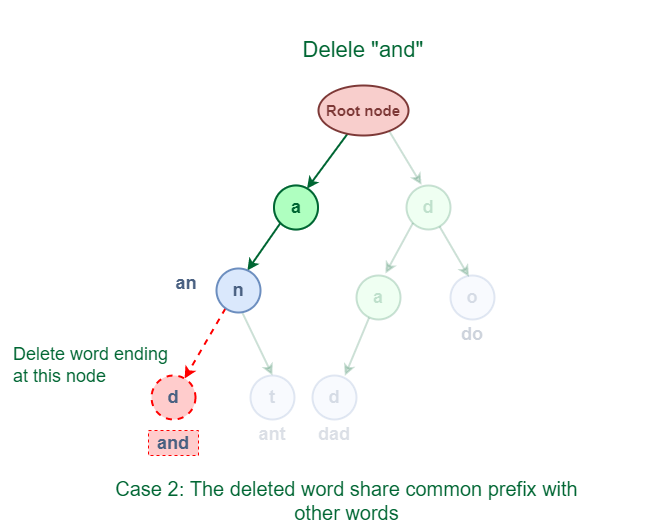
Deletion of word which shares a common prefix with other words in Trie
The solution for this case is to delete all the nodes starting from the end of the prefix to the last character of the given word.
3.3 The deleted word does not share any common prefix with other words in Trie.
As shown in the following figure, the word “geek” does not share any common prefix with any other words.
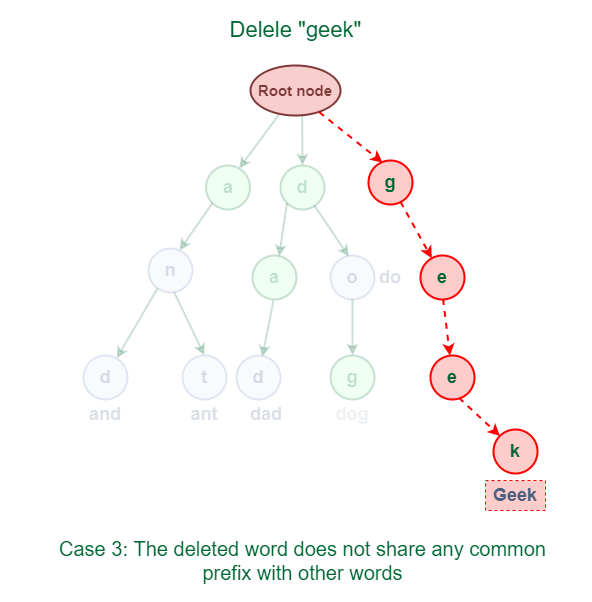
The solution for this case is just to delete all the nodes.
Below is the implementation that handles all the above cases:
C++ bool delete_key(TrieNode* root, string& word) { TrieNode* currentNode = root; TrieNode* lastBranchNode = NULL; char lastBranchChar = 'a'; for (auto c : word) { if (currentNode->childNode[c - 'a'] == NULL) { return false; } else { int count = 0; for (int i = 0; i < 26; i++) { if (currentNode->childNode[i] != NULL) count++; } if (count > 1) { lastBranchNode = currentNode; lastBranchChar = c; } currentNode = currentNode->childNode[c - 'a']; } } int count = 0; for (int i = 0; i < 26; i++) { if (currentNode->childNode[i] != NULL) count++; } // Case 1: The deleted word is a prefix of other words // in Trie. if (count > 0) { currentNode->wordCount--; return true; } // Case 2: The deleted word shares a common prefix with // other words in Trie. if (lastBranchNode != NULL) { lastBranchNode->childNode[lastBranchChar] = NULL; return true; } // Case 3: The deleted word does not share any common // prefix with other words in Trie. else { root->childNode[word[0]] = NULL; return true; } } public class TrieNode { TrieNode[] childNode; int wordCount; public TrieNode() { this.childNode = new TrieNode[26]; this.wordCount = 0; } } public class Trie { TrieNode root; public Trie() { this.root = new TrieNode(); } public boolean deleteKey(String word) { TrieNode currentNode = root; TrieNode lastBranchNode = null; char lastBranchChar = 'a'; for (char c : word.toCharArray()) { if (currentNode.childNode[c - 'a'] == null) { // If the current node has no child, the word is not present return false; } else { int count = 0; // Count the number of non-null child nodes for (int i = 0; i < 26; i++) { if (currentNode.childNode[i] != null) count++; } if (count > 1) { // If there are more than one child, store the last branch information lastBranchNode = currentNode; lastBranchChar = c; } currentNode = currentNode.childNode[c - 'a']; } } int count = 0; // Count the number of non-null child nodes at the last character for (int i = 0; i < 26; i++) { if (currentNode.childNode[i] != null) count++; } // Case 1: The deleted word is a prefix of other words in Trie. if (count > 0) { // Decrement the word count and indicate successful deletion currentNode.wordCount--; return true; } // Case 2: The deleted word shares a common prefix with other words in Trie. if (lastBranchNode != null) { // Remove the link to the deleted word lastBranchNode.childNode[lastBranchChar - 'a'] = null; return true; } // Case 3: The deleted word does not share any common prefix with other words in Trie. else { // Remove the link to the deleted word from the root root.childNode[word.charAt(0) - 'a'] = null; return true; } } } def delete_key(root, word): current_node = root last_branch_node = None last_branch_char = 'a' # loop through each character in the word for c in word: # if the current node doesn't have a child with the current character, # return False as the word is not present in Trie if current_node.childNode[ord(c) - ord('a')] is None: return False else: count = 0 # count the number of children nodes of the current node for i in range(26): if current_node.childNode[i] is not None: count += 1 # if the count of children is more than 1, # store the node and the current character if count > 1: last_branch_node = current_node last_branch_char = c current_node = current_node.childNode[ord(c) - ord('a')] count = 0 # count the number of children nodes of the current node for i in range(26): if current_node.childNode[i] is not None: count += 1 # Case 1: The deleted word is a prefix of other words in Trie if count > 0: current_node.wordCount -= 1 return True # Case 2: The deleted word shares a common prefix with other words in Trie if last_branch_node is not None: last_branch_node.childNode[ord(last_branch_char) - ord('a')] = None return True # Case 3: The deleted word does not share any common prefix with other words in Trie else: root.childNode[ord(word[0]) - ord('a')] = None return True public bool delete_key(TrieNode root, string word) { TrieNode current_node = root; TrieNode last_branch_node = null; char last_branch_char = 'a'; // loop through each character in the word foreach (char c in word) { // if the current node doesn't have a child with the current character, // return False as the word is not present in Trie if (current_node.childNode[c - 'a'] == null) { return false; } else { int count = 0; // count the number of children nodes of the current node for (int i = 0; i < 26; i++) { if (current_node.childNode[i] != null) { count++; } } // if the count of children is more than 1, // store the node and the current character if (count > 1) { last_branch_node = current_node; last_branch_char = c; } current_node = current_node.childNode[c - 'a']; } } int wordCount = 0; // count the number of children nodes of the current node for (int i = 0; i < 26; i++) { if (current_node.childNode[i] != null) { wordCount++; } } // Case 1: The deleted word is a prefix of other words in Trie if (wordCount > 0) { current_node.wordCount--; return true; } // Case 2: The deleted word shares a common prefix with other words in Trie if (last_branch_node != null) { last_branch_node.childNode[last_branch_char - 'a'] = null; return true; } // Case 3: The deleted word does not share any common prefix with other words in Trie else { root.childNode[word[0] - 'a'] = null; return true; } } //This code is contributed by shivamsharma215 function delete_key(root, word) { let currentNode = root; let lastBranchNode = null; let lastBrachChar = 'a'; for (let c of word) { if (currentNode.childNode[c.charCodeAt(0) - 'a'.charCodeAt(0)] === null) { return false; } else { let count = 0; for (let i = 0; i < 26; i++) { if (currentNode.childNode[i] !== null) { count++; } } if (count > 1) { lastBranchNode = currentNode; lastBrachChar = c; } currentNode = currentNode.childNode[c.charCodeAt(0) - 'a'.charCodeAt(0)]; } } let count = 0; for (let i = 0; i < 26; i++) { if (currentNode.childNode[i] !== null) { count++; } } // Case 1: The deleted word is a prefix of other words // in Trie. if (count > 0) { currentNode.wordCount--; return true; } // Case 2: The deleted word shares a common prefix with // other words in Trie. if (lastBranchNode !== null) { lastBranchNode.childNode[lastBrachChar] = null; return true; } // Case 3: The deleted word does not share any common // prefix with other words in Trie. else { root.childNode[word[0].charCodeAt(0) - 'a'.charCodeAt(0)] = null; return true; } } //This code is contributed by shivamsharma215 Implement Trie Data Structure?
Algorithm:
- Create a root node with the help of TrieNode() constructor.
- Store a collection of strings that we have to insert in the trie in a vector of strings say, arr.
- Inserting all strings in Trie with the help of the insertkey() function,
- Search strings from searchQueryStrings with the help of search_key() function.
- Delete the strings present in the deleteQueryStrings with the help of delete_key.
C++ #include <bits/stdc++.h> using namespace std; struct TrieNode { // pointer array for child nodes of each node TrieNode* childNode[26]; int wordCount; TrieNode() { // constructor // initialize the wordCnt variable with 0 // initialize every index of childNode array with // NULL wordCount = 0; for (int i = 0; i < 26; i++) { childNode[i] = NULL; } } }; void insert_key(TrieNode* root, string& key) { // Initialize the currentNode pointer // with the root node TrieNode* currentNode = root; // Iterate across the length of the string for (auto c : key) { // Check if the node exist for the current // character in the Trie. if (currentNode->childNode[c - 'a'] == NULL) { // If node for current character does not exist // then make a new node TrieNode* newNode = new TrieNode(); // Keep the reference for the newly created // node. currentNode->childNode[c - 'a'] = newNode; } // Now, move the current node pointer to the newly // created node. currentNode = currentNode->childNode[c - 'a']; } // Increment the wordEndCount for the last currentNode // pointer this implies that there is a string ending at // currentNode. currentNode->wordCount++; } bool search_key(TrieNode* root, string& key) { // Initialize the currentNode pointer // with the root node TrieNode* currentNode = root; // Iterate across the length of the string for (auto c : key) { // Check if the node exist for the current // character in the Trie. if (currentNode->childNode[c - 'a'] == NULL) { // Given word does not exist in Trie return false; } // Move the currentNode pointer to the already // existing node for current character. currentNode = currentNode->childNode[c - 'a']; } return (currentNode->wordCount > 0); } bool delete_key(TrieNode* root, string& word) { TrieNode* currentNode = root; TrieNode* lastBranchNode = NULL; char lastBrachChar = 'a'; for (auto c : word) { if (currentNode->childNode[c - 'a'] == NULL) { return false; } else { int count = 0; for (int i = 0; i < 26; i++) { if (currentNode->childNode[i] != NULL) count++; } if (count > 1) { lastBranchNode = currentNode; lastBrachChar = c; } currentNode = currentNode->childNode[c - 'a']; } } int count = 0; for (int i = 0; i < 26; i++) { if (currentNode->childNode[i] != NULL) count++; } // Case 1: The deleted word is a prefix of other words // in Trie. if (count > 0) { currentNode->wordCount--; return true; } // Case 2: The deleted word shares a common prefix with // other words in Trie. if (lastBranchNode != NULL) { lastBranchNode->childNode[lastBrachChar] = NULL; return true; } // Case 3: The deleted word does not share any common // prefix with other words in Trie. else { root->childNode[word[0]] = NULL; return true; } } // Driver code int main() { // Make a root node for the Trie TrieNode* root = new TrieNode(); // Stores the strings that we want to insert in the // Trie vector<string> inputStrings = { "and", "ant", "do", "geek", "dad", "ball" }; // number of insert operations in the Trie int n = inputStrings.size(); for (int i = 0; i < n; i++) { insert_key(root, inputStrings[i]); } // Stores the strings that we want to search in the Trie vector<string> searchQueryStrings = { "do", "geek", "bat" }; // number of search operations in the Trie int searchQueries = searchQueryStrings.size(); for (int i = 0; i < searchQueries; i++) { cout << "Query String: " << searchQueryStrings[i] << "\n"; if (search_key(root, searchQueryStrings[i])) { // the queryString is present in the Trie cout << "The query string is present in the " "Trie\n"; } else { // the queryString is not present in the Trie cout << "The query string is not present in " "the Trie\n"; } } // stores the strings that we want to delete from the // Trie vector<string> deleteQueryStrings = { "geek", "tea" }; // number of delete operations from the Trie int deleteQueries = deleteQueryStrings.size(); for (int i = 0; i < deleteQueries; i++) { cout << "Query String: " << deleteQueryStrings[i] << "\n"; if (delete_key(root, deleteQueryStrings[i])) { // The queryString is successfully deleted from // the Trie cout << "The query string is successfully " "deleted\n"; } else { // The query string is not present in the Trie cout << "The query string is not present in " "the Trie\n"; } } return 0; } # Trie implementation in Python class TrieNode: def __init__(self): # pointer array for child nodes of each node self.childNode = [None] * 26 self.wordCount = 0 def insert_key(root, key): # Initialize the currentNode pointer with the root node currentNode = root # Iterate across the length of the string for c in key: # Check if the node exist for the current character in the Trie. if not currentNode.childNode[ord(c) - ord('a')]: # If node for current character does not exist # then make a new node newNode = TrieNode() # Keep the reference for the newly created node. currentNode.childNode[ord(c) - ord('a')] = newNode # Now, move the current node pointer to the newly created node. currentNode = currentNode.childNode[ord(c) - ord('a')] # Increment the wordEndCount for the last currentNode # pointer this implies that there is a string ending at currentNode. currentNode.wordCount += 1 def search_key(root, key): # Initialize the currentNode pointer with the root node currentNode = root # Iterate across the length of the string for c in key: # Check if the node exist for the current character in the Trie. if not currentNode.childNode[ord(c) - ord('a')]: # Given word does not exist in Trie return False # Move the currentNode pointer to the already existing node for current character. currentNode = currentNode.childNode[ord(c) - ord('a')] return currentNode.wordCount > 0 def delete_key(root, word): currentNode = root lastBranchNode = None lastBrachChar = 'a' for c in word: if not currentNode.childNode[ord(c) - ord('a')]: return False else: count = 0 for i in range(26): if currentNode.childNode[i]: count += 1 if count > 1: lastBranchNode = currentNode lastBrachChar = c currentNode = currentNode.childNode[ord(c) - ord('a')] count = 0 for i in range(26): if currentNode.childNode[i]: count += 1 # Case 1: The deleted word is a prefix of other words in Trie. if count > 0: currentNode.wordCount -= 1 return True # Case 2: The deleted word shares a common prefix with other words in Trie. if lastBranchNode: lastBranchNode.childNode[ord(lastBrachChar) - ord('a')] = None return True # Case 3: The deleted word does not share any common prefix with other words in Trie. else: root.childNode[ord(word[0]) - ord('a')] = None return True # Driver Code if __name__ == '__main__': # Make a root node for the Trie root = TrieNode() # Stores the strings that we want to insert in the Trie input_strings = ["and", "ant", "do", "geek", "dad", "ball"] # number of insert operations in the Trie n = len(input_strings) for i in range(n): insert_key(root, input_strings[i]) # Stores the strings that we want to search in the Trie search_query_strings = ["do", "geek", "bat"] # number of search operations in the Trie search_queries = len(search_query_strings) for i in range(search_queries): print("Query String:", search_query_strings[i]) if search_key(root, search_query_strings[i]): # the queryString is present in the Trie print("The query string is present in the Trie") else: # the queryString is not present in the Trie print("The query string is not present in the Trie") # stores the strings that we want to delete from the Trie delete_query_strings = ["geek", "tea"] # number of delete operations from the Trie delete_queries = len(delete_query_strings) for i in range(delete_queries): print("Query String:", delete_query_strings[i]) if delete_key(root, delete_query_strings[i]): # The queryString is successfully deleted from the Trie print("The query string is successfully deleted") else: # The query string is not present in the Trie print("The query string is not present in the Trie") # This code is contributed by Vikram_Shirsat // C# code addition using System; using System.Collections; using System.Collections.Generic; using System.Linq; class TrieNode { public TrieNode[] ChildNode = new TrieNode[26]; public int WordCount; public TrieNode() { WordCount = 0; for (int i = 0; i < 26; i++) { ChildNode[i] = null; } } } class Program { static void InsertKey(TrieNode root, string key) { TrieNode currentNode = root; foreach (char c in key) { if (currentNode.ChildNode[c - 'a'] == null) { TrieNode newNode = new TrieNode(); currentNode.ChildNode[c - 'a'] = newNode; } currentNode = currentNode.ChildNode[c - 'a']; } currentNode.WordCount++; } static bool SearchKey(TrieNode root, string key) { TrieNode currentNode = root; foreach (char c in key) { if (currentNode.ChildNode[c - 'a'] == null) { return false; } currentNode = currentNode.ChildNode[c - 'a']; } return (currentNode.WordCount > 0); } static bool DeleteKey(TrieNode root, string word) { TrieNode currentNode = root; TrieNode lastBranchNode = null; char lastBranchChar = 'a'; foreach (char c in word) { if (currentNode.ChildNode[c - 'a'] == null) { return false; } else { int count = 0; for (int i = 0; i < 26; i++) { if (currentNode.ChildNode[i] != null) count++; } if (count > 1) { lastBranchNode = currentNode; lastBranchChar = c; } currentNode = currentNode.ChildNode[c - 'a']; } } int leafCount = 0; for (int i = 0; i < 26; i++) { if (currentNode.ChildNode[i] != null) leafCount++; } if (leafCount > 0) { currentNode.WordCount--; return true; } if (lastBranchNode != null) { lastBranchNode.ChildNode[lastBranchChar - 'a'] = null; return true; } else { root.ChildNode[word[0] - 'a'] = null; return true; } } static void Main() { TrieNode root = new TrieNode(); string[] inputStrings = { "and", "ant", "do", "geek", "dad", "ball" }; foreach (string str in inputStrings) { InsertKey(root, str); } string[] searchQueryStrings = { "do", "geek", "bat" }; foreach (string str in searchQueryStrings) { Console.WriteLine("Query String: " + str); if (SearchKey(root, str)) { Console.WriteLine("The query string is present in the Trie"); } else { Console.WriteLine("The query string is not present in the Trie"); } } string[] deleteQueryStrings = { "geek", "tea" }; foreach (string str in deleteQueryStrings) { Console.WriteLine("Query String: " + str); if (DeleteKey(root, str)) { Console.WriteLine("The query string is successfully deleted"); } else{ // The query string is not present in the Trie Console.WriteLine("The query string is not present in the Trie"); } } } } // The code is contributed by Nidhi goel. class TrieNode{ constructor(){ //pointer array for child nodes of each node this.childNode = new Array(26).fill(null); this.wordCount = 0; } } // function to insert key in Trie function insertKey(root, key){ // initializing currentNode with root node let currentNode = root; // iterating over length of string for(let i = 0; i < key.length; i++){ // check if node exist for current character in Trie if(!currentNode.childNode[key.charCodeAt(i) - 97]){ // if node doesn't exist then create new node let newNode = new TrieNode(); // keeping reference for newly created node currentNode.childNode[key.charCodeAt(i) - 97] = newNode; } // now moving currentNode pointer to newly created node currentNode = currentNode.childNode[key.charCodeAt(i) - 97]; } // incrementing wordCount for last currentNode pointer // implies that there is a string ending at currentNode currentNode.wordCount++; } // function to search key in Trie function searchKey(root, key){ // initializing currentNode with root node let currentNode = root; // iterating over length of string for(let i = 0; i < key.length; i++){ // check if node exist for current character in Trie if(!currentNode.childNode[key.charCodeAt(i) - 97]){ // given word does not exist in Trie return false; } // move currentNode pointer to already existing node for current character currentNode = currentNode.childNode[key.charCodeAt(i) - 97]; } return currentNode.wordCount > 0; } // function to delete key from Trie function deleteKey(root, word){ let currentNode = root; let lastBranchNode = null; let lastBranchChar = 'a'; for(let i = 0; i < word.length; i++){ // check if node exist for current character in Trie if(!currentNode.childNode[word.charCodeAt(i) - 97]){ return false; } // check if there is more than one branch at current node else{ let count = 0; for(let j = 0; j < 26; j++){ if(currentNode.childNode[j]){ count++; } } // if there is more than one branch then store the node and character if(count > 1){ lastBranchNode = currentNode; lastBranchChar = word[i]; } // move currentNode pointer to already existing node for current character currentNode = currentNode.childNode[word.charCodeAt(i) - 97]; } } // checking if there is more than one branch at current node let count = 0; for(let i = 0; i < 26; i++){ if(currentNode.childNode[i]){ count++ } } // Case 1: The deleted word is a prefix of other words in Trie if(count > 0){ currentNode.wordCount--; return true; } // Case 2: The deleted word shares a common prefix with other words in Trie else if(lastBranchNode){ lastBranchNode.childNode[lastBranchChar.charCodeAt(0) - 97] = null; return true; } // Case 3: The deleted word does not share any common prefix with other words in Trie else{ root.childNode[word.charCodeAt(0) - 97] = null; return true; } } // driver code function main(){ // making a root node for Trie let root = new TrieNode(); // stores the strings that we want to insert in Trie let inputStrings = ["and", "ant", "do", "geek", "dad", "ball"]; // number of insert operations in Trie let n = inputStrings.length; for(let i = 0; i < n; i++){ insertKey(root, inputStrings[i]); } // stores the strings that we want to search in Trie let searchQueryStrings = ["do", "geek", "bat"]; // number of search operations in Trie let searchQueries = searchQueryStrings.length; for(let i = 0; i < searchQueries; i++){ console.log("Query String:", searchQueryStrings[i]); if(searchKey(root, searchQueryStrings[i])){ // the queryString is present in the Trie console.log("The query string is present in the Trie"); } else{ // the queryString is not present in the Trie console.log("The query string is not present in the Trie"); } } // stores the strings that we want to delete from the Trie let deleteQueryStrings = ["geek", "tea"]; // number of delete operations from the Trie let deleteQueries = deleteQueryStrings.length; for(let i = 0; i < deleteQueries; i++){ console.log("Query String:", deleteQueryStrings[i]); if(deleteKey(root, deleteQueryStrings[i])){ // the queryString is successfully deleted from the Trie console.log("The query string is successfully deleted"); } else{ // the queryString is not present in the Trie console.log("The query string is not present in the Trie"); } } } main(); OutputQuery String: do The query string is present in the Trie Query String: geek The query string is present in the Trie Query String: bat The query string is not present in the Trie Query String: geek The query string is successfully deleted Query String: tea The query string is not present in the Trie
Complexity Analysis of Trie Data Structure
| Operation | Time Complexity |
|---|
| Insertion | O(n) Here n is the length of string to be searched |
|---|
| Searching | O(n) |
|---|
| Deletion | O(n) |
|---|
Note: In the above complexity table ‘n’, ‘m’ represents the size of the string and the number of strings that are stored in the trie.
1. Autocomplete Feature: Autocomplete provides suggestions based on what you type in the search box. Trie data structure is used to implement autocomplete functionality.
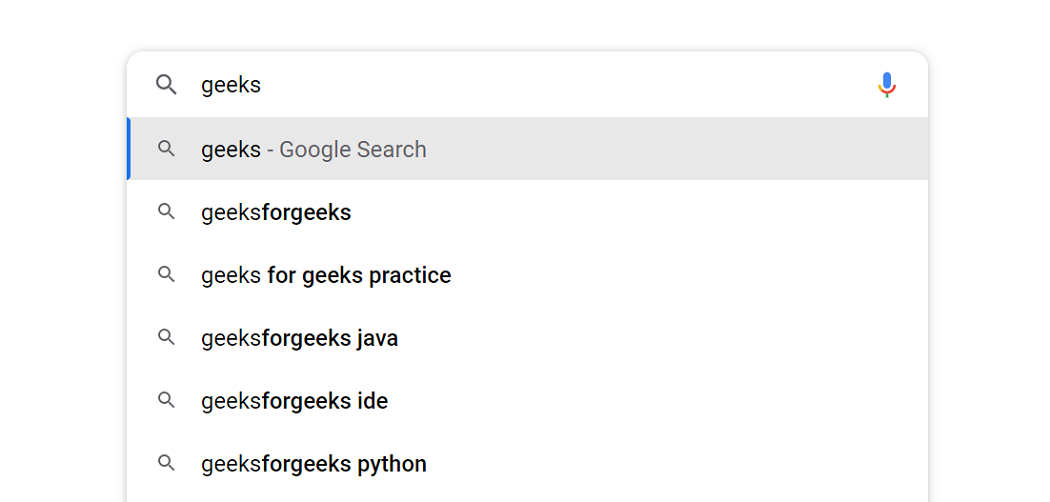
Autocomplete feature of Trie Data Structure
2. Spell Checkers: If the word typed does not appear in the dictionary, then it shows suggestions based on what you typed.
It is a 3-step process that includes :
- Checking for the word in the data dictionary.
- Generating potential suggestions.
- Sorting the suggestions with higher priority on top.
Trie stores the data dictionary and makes it easier to build an algorithm for searching the word from the dictionary and provides the list of valid words for the suggestion.
3. Longest Prefix Matching Algorithm(Maximum Prefix Length Match): This algorithm is used in networking by the routing devices in IP networking. Optimization of network routes requires contiguous masking that bound the complexity of lookup a time to O(n), where n is the length of the URL address in bits.
To speed up the lookup process, Multiple Bit trie schemes were developed that perform the lookups of multiple bits faster.
- Trie allows us to input and finds words in O(n) time, where n is the length of a single word. It is faster as compared to both hash tables and binary search trees.
- It provides alphabetical filtering of entries by the key of the node and hence makes it easier to print all words in alphabetical order.
- Prefix search/Longest prefix matching can be efficiently done with the help of trie data structure.
- Since trie doesn’t need any hash function for its implementation so they are generally faster than hash tables for small keys like integers and pointers.
- Tries support ordered iteration whereas iteration in a hash table will result in pseudorandom order given by the hash function which is usually more cumbersome.
- Deletion is also a straightforward algorithm with O(n) as its time complexity, where n is the length of the word to be deleted.
Disadvantages of Trie data structure:
- The main disadvantage of the trie is that it takes a lot of memory to store all the strings. For each node, we have too many node pointers which are equal to the no of characters in the worst case.
- An efficiently constructed hash table(i.e. a good hash function and a reasonable load factor) has O(1) as lookup time which is way faster than O(l) in the case of a trie, where l is the length of the string.
Top Interview problems on Trie data structure:
Conclusion:
Our discussion so far has led us to the conclusion that the Trie data structure is a Tree based data structure that is used for storing some collection of strings and performing efficient search operations on them and we have also discussed the various advantage and applications of trie data structure.
Related articles:
Similar Reads
Advanced Data Structures
Advanced Data Structures refer to complex and specialized arrangements of data that enable efficient storage, retrieval, and manipulation of information in computer science and programming. These structures go beyond basic data types like arrays and lists, offering sophisticated ways to organize and
3 min read
Generic Linked List in C
A generic linked list is a type of linked list that allows the storage of different types of data in a single linked list structure, providing more versatility and reusability in various applications. Unlike C++ and Java, C doesn't directly support generics. However, we can write generic code using
5 min read
Memory efficient doubly linked list
We need to implement a doubly linked list with the use of a single pointer in each node. For that we are given a stream of data of size n for the linked list, your task is to make the function insert() and getList(). The insert() function pushes (or inserts at the beginning) the given data in the li
9 min read
XOR Linked List - A Memory Efficient Doubly Linked List | Set 1
In this post, we're going to talk about how XOR linked lists are used to reduce the memory requirements of doubly-linked lists. We know that each node in a doubly-linked list has two pointer fields which contain the addresses of the previous and next node. On the other hand, each node of the XOR lin
15+ min read
XOR Linked List – A Memory Efficient Doubly Linked List | Set 2
In the previous post, we discussed how a Doubly Linked can be created using only one space for the address field with every node. In this post, we will discuss the implementation of a memory-efficient doubly linked list. We will mainly discuss the following two simple functions. A function to insert
10 min read
Skip List - Efficient Search, Insert and Delete in Linked List
A skip list is a data structure that allows for efficient search, insertion and deletion of elements in a sorted list. It is a probabilistic data structure, meaning that its average time complexity is determined through a probabilistic analysis. In a skip list, elements are organized in layers, with
6 min read
Self Organizing List | Set 1 (Introduction)
The worst case search time for a sorted linked list is O(n). With a Balanced Binary Search Tree, we can skip almost half of the nodes after one comparison with root. For a sorted array, we have random access and we can apply Binary Search on arrays. One idea to make search faster for Linked Lists is
3 min read
Unrolled Linked List | Set 1 (Introduction)
Like array and linked list, the unrolled Linked List is also a linear data structure and is a variant of a linked list. Why do we need unrolled linked list? One of the biggest advantages of linked lists over arrays is that inserting an element at any location takes only O(1). However, the catch here
10 min read