Integral of Cos x is equal to Sin x + C. Integral of a function is the process of finding the area under the curve. Integration of Cos x gives the area of the region covered by the cosine trigonometric function. The integral also called the Antiderivative of a function, exists when the function is differentiable. Integration of Cos x is possible as the cosine function is also differentiable in its domain.
In this article, we will learn what is Integral of cos x, the formula of the Integral of cos x, and how to integrate cos x.
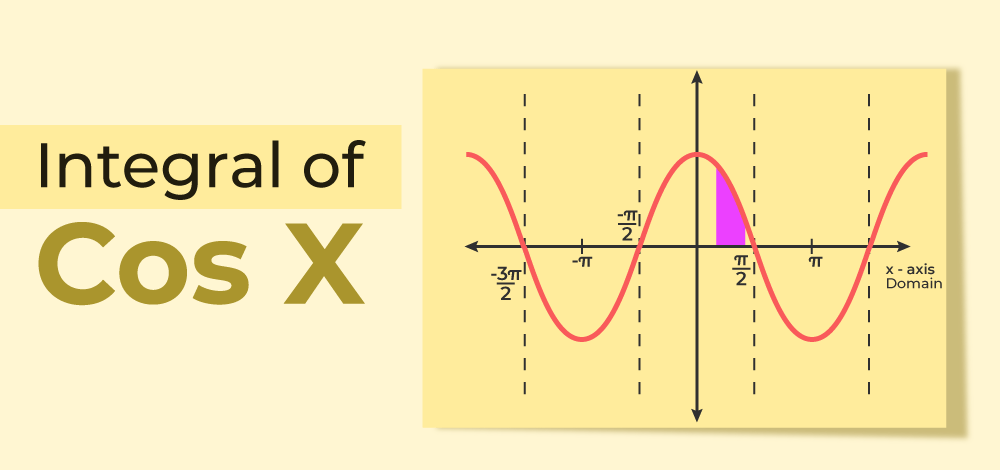
What is Integral of Cos x?
Integral of cos x is sin x + C where C is constant of integration. Integration of Cosine exists as cosine is a differentiable function. The Differentiation and Integration are reverse processes in calculus. When we know the derivate of a function, we can derive the function with the help of integration but with a constant as the constants are eliminated while finding out the derivate because derivative of a constant is 0. So we add a constant 'c' whenever we integrate. One of the applications of Integration is it is used to find area under the curve.

Integral of cos x gives information about the area under the curve of cos x and its definite integral gives area under the graph of cos x within specified bounds.
The integral of Cos x is sin x. Hence, the formula of integral of cos x is given as:
Since, d(sin x)/dx = cos x
∫cos x dx = sin x + c
The Integral of Cos x Formula can be derived using following two ways:
- By Fundamental Theorem of Calculus
- By Trigonometric Substitution
Integral of Cos x by Fundamental Theorem of Calculus
The proof of integration of cos x using Fundamental Theorem of Calculus
Let us assume
y = cos x
dy/dx = -sin x
We know that : sin2x + cos2x = 1
sin x = √(1-cos2x)
dy/dx = - √(1-cos2x)
dx = dy/-√(1-cos2x)
[ cos x = y]
dx = dy/ -√(1 - y2 )
∫cos x dx = -y.dy / √(1 - y2 )
Let us assume 1 - y2 = t
-2ydy = dt
Substituting it in integral of cos x
∫cos x dx = dt / 2√t
∫cos x dx = √t
∫cos x dx = √(1 - y2)
∫cos x dx = √(1 - cos2x)
∫cos x dx = √sin2x
∫cos x dx = sin x
Hence Proved.
Integral of Cos x by Trigonometric Substitution
The proof of cos x using trigonometric substitution is given below:
I = ∫cos x.dx
Let cos x = (eix + e-ix)/2
I = ∫(eix + e-ix)dx / 2
I = ((eix/i) + (e-ix/-i))/2 + c
I = (eix - e-ix)/2i + c
We know that
sin x = (eix - e-ix)/2i
Hence
I = sin x + c
Hence Proved.
Learn,
Definite Integral of cos x
Definite Integral of cos x gives area under the graph of cos x with in given bounds [a,b]. It is given by ∫ab cos xdx where a and b are the limits of integration. Definite Integral formula is given as
∫ab f(x) dx = F(b) - F(a)
Definite Integral of cos x
The definite integral of cos x is given below
∫ab cos xdx = [sin x]ab= sinb - sina
Definite integral of cos x from 0 to π/2
∫π/20cos xdx = [sin x] π/20
= sin π/2 - sin 0
= 1 - 0
= 1
Definite integral of cos x from π/2 to π
∫ππ/2cos xdx = [sin x]ππ/2
= sinπ - sinπ /2
= 0 - 1
= -1
Integral of Cos x Graphical Significance
We know that the integration gives the idea about the area under the curve. Hence, the integral of cos x also gives the area under the cosine curve within a defined range. The area under the cosine curve is shown below:

Area under Cosine Curve from 0 to π/2
Approximate calculation of Area under cosine curve is given as
Area of Triangle = 1/2 × b × h = 1/2 × π/2 × 1 = π/4 ≈ 0.8
Area under cosine curve from 0 to π/2 using integration is given as:
Area = ∫π/20cos xdx = [sin x] π/20
= sin π/2 - sin 0
= 1 - 0
= 1
Area under Cosine Curve from 0 to π
Approximate calculation of Area under Cosine Curve is given as:
Area of Triangle 1 + Area of Triangle 2 = (1/2 × π/2 × 1) - (1/2 × π/2 × 1) = 0
Area under Cosine curve using Integration is given as:
Area = ∫π0cos xdx = [sin x] π0
= sin π - sin 0
= 0 - 0
= 0
Hence, we verified that the integration of cos x gives the area under the cosine curve under the defined limits
Also, Check
Integral of Cos x Solved Examples
Example 1. I = ∫2cos x dx/3sin2x . Evaluate I.
Solution:
I = 2/3 ∫cosec x.cot x dx
I = (-2cosec x/3) + c
Example 2. Find the integral of sin x.cos x
Solution:
I = ∫(2sin x.cos x)/2
I = ∫sin2x/2
I = -cos2x/4 + c
Example 3. Find ∫(sin2x - cos2x).dx/(sin x cos x)
Solution:
I = ∫(sin2xdx/sin x.cos x) - ∫(cos2xdx/sin x.cos x)
I = ∫tan x dx - ∫cot x dx
= log|sec x|-[-log|cosec x|] + c
= log|sec x| + log|cosec x| + c
Example 4. Find ∫(sin2x - cos2x)dx / sin2x*cos2x.
Solution:
I = ∫sec2xdx - ∫cosec2xdx
= tan x + cotx + c
Example 5. Find ∫sin6xdx/cos8x.
Solution:
I = ∫sin6xdx/cos8x
= ∫tan6x.sec2xdx
Let tan x = t
sec2x dx = dt
I = ∫t6 dt
I = t7/7 + c
I = tan7x/7 + c
Example 6. Find ∫(cos x)2dx.
Solution:
cos2x = 2cos2x - 1
I = ∫(cos2x+1)dx/2
= (sin2x)/(2*2) + (x/2) + c
= sin2x/4 + x/2 + c
Example 7. Find ∫(cos x)-1 dx.
Solution:
By using ILATE
I = ∫1.cos-1x.dx
= cos-1x.x + ∫(-1)/(√1-x2) * xdx
= xcos-1x + (1/2) * ∫(2x dx)/(√(1-x2)
Let 1 - x2 = t
-2xdx = dt
= xcos-1x -(1/2)*t1/2/(1/2) + c
= xcos-1x - √t + c
= xcos-1x - √(1 - x2) + c
Example 8. Evaluate I = ∫(cos2x - cos2a)dx/(cos x - cos a).
Solution:
I = ∫(cos2x - cos2a)dx/(cos x-cos a)
We know that cos2x = 2cos2x - 1
= ∫((2cos2x - 1) - (2cos2a - 1))dx/(cos x - cos a)
= ∫(2(cos2x - cos2a))dx/(cos x - cos a)
= ∫(2(cos x + cos a)(cos x - cos a)dx/(cos x - cos a)
= ∫2(cos x + cos a)dx
= 2(sin x + xcos a) + c
Integral of Cos x Practice Problems
Try out the following practice problems on Integration of Cos x
Q1. Evaluate ∫dx/sin2x * cos2x.
Q2. Find the integral of cos-1(sin x).
Q3. Find ∫2.dx/(1 + cos2x).
Q4. Find the value of ∫cos3x.
Q5. Evaluate ∫dx/(sin4x + cos4x).
Summary
To find the integral of cos(x), we look for a function whose derivative is cos(x). The function that satisfies this condition is sin(x), since the derivative of sin(x) is cos(x). Therefore, the integral of cos(x) with respect to x is sin(x) plus a constant of integration, C, which accounts for any constant term that would disappear when differentiating. Thus, the integral of cos(x) is sin(x)+C.
Similar Reads
Integral of Cosec x Integral of the Cosec x is ∫cosec x dx = ln |cosec x - cot x| + C. Cosec is also called the cosecant function. Its integration is denoted as ∫(cosec x).dx. It is one of the fundamental integrations involving trigonometric functions. Cosec x is the reciprocal function of sin x. In this article, we wi
6 min read
Integral of Cot x Integral of Cot x is ln |sin x| + C. Cot x is among one of the trigonometric functions that is the ratio of cosine and sine. The integral of cot x is mathematically represented as ∫cot x dx = ln |sinx| + C. In this article, we will explore the integral of cot x, the integral of cot x formula, the de
7 min read
Integral of x The integral of x with respect to x is x2/2 + C, where C is the constant of integration.The integral of x is a fundamental concept in calculus, representing the area under the curve of the function x on a graph. In simple terms, finding the integral of x means determining a function whose derivative
4 min read
Integral of 1/x^3 {\Huge \int \frac{1}{x^3} \, dx = -\frac{1}{2x^2} + C}Integrating functions is a fundamental aspect of Integral calculus that provides valuable insights into various mathematical problems. Calculating integrals is an essential skill in calculus, and understanding the techniques for different integra
1 min read
Integral of 1/x^2 Integrals are essential in various fields such as physics, engineering, economics, and statistics. They help solve problems related to motion, area, volume, and total accumulation, making them a powerful tool for understanding and modeling continuous change.Integral of 1/x2 is - (1/x) + CIn this art
3 min read