Height and Depth of a node in a Binary Tree

Last Updated : 03 Apr, 2025

Given a Binary Tree consisting of n nodes and a integer k, the task is to find the depth and height of the node with value k in the Binary Tree.

Note:

The depth of a node is the number of edges present in path from the root node of a tree to that node.
The height of a node is the maximum number of edges from that node to a leaf node in its subtree.

Examples:

Input: k = 25,

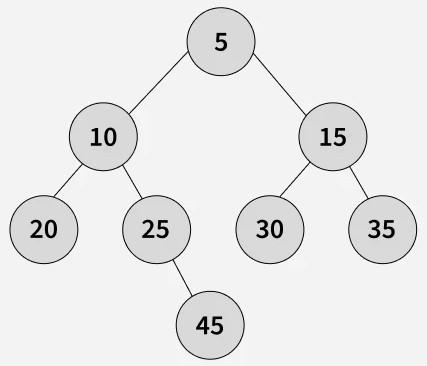
Output: Depth of node 25 = 2
Height of node 25 = 1
Explanation: The number of edges in the path from root node to the node 25 is 2. Therefore, depth of the node 25 is 2.
The number of edges in the longest path connecting the node 25 to any leaf node is 1. Therefore, height of the node 25 is 1.

Input: k = 10,

Output: Depth of node 10 = 1
Height of node 10 = 2
Explanation: The number of edges in the path from root node to the node 10 is 1.
The number of edges in the longest path connecting the node 10 to any leaf node is 2.

Table of Content

[Approach 1] Using Recursion – O(n) time and O(h) space

Depth of a node K (of a Binary Tree) = Number of edges in the path connecting the root to the node K = Number of ancestors of K (excluding K itself).

Follow the steps below to find the depth of the given node:

If the tree is empty, print -1.
Otherwise, perform the following steps:
- Initialize a variable, say dist as -1.
- Check if the node K is equal to the given node.
- Otherwise, check if it is present in either of the subtrees, by recursively checking for the left and right subtrees respectively.
- If found to be true, print the value of dist + 1.
- Otherwise, print dist.

Height of a node K (of a Binary Tree) = Maximum number of edges from that node to a leaf node in its subtree.

Follow the steps below to find the height of the given node:

If the tree is empty, print -1.
Otherwise, perform the following steps:
- Calculate the height of the left subtree recursively.
- Calculate the height of the right subtree recursively.
- Update height of the current node by adding 1 to the maximum of the two heights obtained in the previous step. Store the height in a variable, say ans.
- If the current node is equal to the given node k, print the value of ans as the required answer.

C++

#include <bits/stdc++.h> using namespace std;  // Structure of a Binary Tree Node struct Node {     int data;     Node *left, *right;     Node(int item) {         data = item;         left = right = nullptr;     } };  int findDepth(Node* root, int x) {     // Base case     if (root == nullptr)         return -1;      int dist = -1;      // Check if x is current node=     if ((root->data == x)          // Otherwise, check if x is         // present in the left subtree         || (dist = findDepth(root->left, x)) >= 0          // Otherwise, check if x is         // present in the right subtree         || (dist = findDepth(root->right, x)) >= 0)          // Return depth of the node         return dist + 1;      return dist; }  int findHeightUtil(Node* root, int x,                    int& height) {     if (root == nullptr) {         return -1;     }      // Store the maximum height of     // the left and right subtree     int leftHeight = findHeightUtil(         root->left, x, height);      int rightHeight         = findHeightUtil(             root->right, x, height);      // Update height of the current node     int ans = max(leftHeight, rightHeight) + 1;      // If current node is the required node     if (root->data == x)         height = ans;      return ans; }  int findHeight(Node* root, int x) {     // Store the height of     // the given node     int h = -1;      // Stores height of the Tree     int maxHeight = findHeightUtil(root, x, h);      // Return the height     return h; }  int main() {     Node* root = new Node(5);     root->left = new Node(10);     root->right = new Node(15);     root->left->left = new Node(20);     root->left->right = new Node(25);     root->left->right->right = new Node(45);     root->right->left = new Node(30);     root->right->right = new Node(35);      int k = 25;      cout << "Depth: "          << findDepth(root, k) << "\n";      cout << "Height: " << findHeight(root, k);      return 0; }

Java

// Structure of a Binary Tree Node class Node {     int data;     Node left, right;     Node(int item) {         data = item;         left = right = null;     } }  public class GfG{      int findDepth(Node root, int x) {                  // Base case         if (root == null)             return -1;          // Initialize distance as -1         int dist = -1;          // Check if x is current node         if ((root.data == x)             || (dist = findDepth(root.left, x)) >= 0             || (dist = findDepth(root.right, x)) >= 0)             // Return depth of the node             return dist + 1;          return dist;     }      int findHeightUtil(Node root, int x, int[] height) {         // Base Case         if (root == null) {             return -1;         }          // Store the maximum height of the left and right subtree         int leftHeight = findHeightUtil(root.left, x, height);         int rightHeight = findHeightUtil(root.right, x, height);          // Update height of the current node         int ans = Math.max(leftHeight, rightHeight) + 1;          // If current node is the required node         if (root.data == x)             height[0] = ans;          return ans;     }      int findHeight(Node root, int x) {         // Store the height of the given node         int[] h = {-1};          // Stores height of the Tree         findHeightUtil(root, x, h);          // Return the height         return h[0];     }      public static void main(String[] args) {         Node root = new Node(5);         root.left = new Node(10);         root.right = new Node(15);         root.left.left = new Node(20);         root.left.right = new Node(25);         root.left.right.right = new Node(45);         root.right.left = new Node(30);         root.right.right = new Node(35);          int k = 25;          GfG tree = new GfG();         System.out.println("Depth: " + tree.findDepth(root, k));         System.out.println("Height: " + tree.findHeight(root, k));     } }

Python

class Node:     def __init__(self, data):         self.data = data         self.left = None         self.right = None  # Function to find depth of a given node def find_depth(root, x):     if root is None:         return -1          dist = -1          # Check if x is the current node or     # if it exists in the left or right subtree     if (root.data == x or         (dist := find_depth(root.left, x)) >= 0 or         (dist := find_depth(root.right, x)) >= 0):         return dist + 1          return dist  # Utility function to find height of a given node def find_height_util(root, x, height):     if root is None:         return -1          # Store the maximum height of left and right subtree     left_height = find_height_util(root.left, x, height)     right_height = find_height_util(root.right, x, height)          # Update height of the current node     ans = max(left_height, right_height) + 1          # If current node is the required node, update height     if root.data == x:         height[0] = ans          return ans  # Function to find height of a given node def find_height(root, x):     height = [-1]  # Using a list to                     # store height by reference     find_height_util(root, x, height)     return height[0]  if __name__ == "__main__":     # Construct the tree     root = Node(5)     root.left = Node(10)     root.right = Node(15)     root.left.left = Node(20)     root.left.right = Node(25)     root.left.right.right = Node(45)     root.right.left = Node(30)     root.right.right = Node(35)          k = 25          # Print depth and height of the given node     print("Depth:", find_depth(root, k))     print("Height:", find_height(root, k))

using System; using System.Collections.Generic;  // Structure of a Binary Tree Node class Node {     public int data;     public Node left, right;      public Node(int item) {         data = item;         left = right = null;     } }  class GfG{     int FindDepth(Node root, int x) {                  // Base case         if (root == null)             return -1;          // Initialize distance as -1         int dist = -1;          // Check if x is current node         if ((root.data == x)             || (dist = FindDepth(root.left, x)) >= 0             || (dist = FindDepth(root.right, x)) >= 0)                          // Return depth of the node             return dist + 1;          return dist;     }      int FindHeightUtil(Node root, int x, ref int height) {         // Base Case         if (root == null) {             return -1;         }          // Store the maximum height of the left and right subtree         int leftHeight = FindHeightUtil(root.left, x, ref height);         int rightHeight = FindHeightUtil(root.right, x, ref height);          // Update height of the current node         int ans = Math.Max(leftHeight, rightHeight) + 1;          // If current node is the required node         if (root.data == x)             height = ans;          return ans;     }      int FindHeight(Node root, int x) {         // Store the height of the given node         int h = -1;          // Stores height of the Tree         FindHeightUtil(root, x, ref h);          // Return the height         return h;     }      public static void Main(string[] args) {         Node root = new Node(5);         root.left = new Node(10);         root.right = new Node(15);         root.left.left = new Node(20);         root.left.right = new Node(25);         root.left.right.right = new Node(45);         root.right.left = new Node(30);         root.right.right = new Node(35);          int k = 25;          GfG tree = new GfG();         Console.WriteLine("Depth: " + tree.FindDepth(root, k));         Console.WriteLine("Height: " + tree.FindHeight(root, k));     } }

JavaScript

class Node {     constructor(data) {         this.data = data;         this.left = null;         this.right = null;     } }  // Function to find depth of a given node function findDepth(root, x) {     if (!root) return -1;          let dist = -1;          // Check if x is the current node or     // if it exists in the left or right subtree     if (root.data === x ||         (dist = findDepth(root.left, x)) >= 0 ||         (dist = findDepth(root.right, x)) >= 0) {         return dist + 1;     }          return dist; }  // Utility function to find height of a given node function findHeightUtil(root, x, height) {     if (!root) return -1;          // Store the maximum height of left and right subtree     let leftHeight = findHeightUtil(root.left, x, height);     let rightHeight = findHeightUtil(root.right, x, height);          // Update height of the current node     let ans = Math.max(leftHeight, rightHeight) + 1;          // If current node is the required node, update height     if (root.data === x) height.value = ans;          return ans; }  // Function to find height of a given node function findHeight(root, x) {     let height = { value: -1 }; // Using an object                              // to store height by reference     findHeightUtil(root, x, height);     return height.value; }  // Construct the tree let root = new Node(5); root.left = new Node(10); root.right = new Node(15); root.left.left = new Node(20); root.left.right = new Node(25); root.left.right.right = new Node(45); root.right.left = new Node(30); root.right.right = new Node(35);  let k = 25;  // Print depth and height of the given node console.log("Depth:", findDepth(root, k)); console.log("Height:", findHeight(root, k));

Output

Depth: 2 Height: 1

Time Complexity: O(n)
Auxiliary Space: O(1)

[Approach 2] Using Level Order Traversal – O(n) time and O(n) space

We can calculate the depth of each node using level order traversal by storing the current level as its depth.
To calculate the height of a node k, we find the maximum depth of any leaf node in its subtree.
Then:
Height of node k = (Max depth of leaf in subtree) − (Depth of node k) − 1

Algorithm:

Initialize height and depth variable with -1;
Initialize a queue and a level variable with 0 and push the root in the queue.
When the value of frontNode is equal to the target k, we stop processing the nodes at that level and clear the queue to only focus on the children of the node k. This ensures that we find the furthest leaf node in the subtree of k.
So the value of depth will be equal to current level.
After completion we can calculate the value of height using height = level – depth – 1;
Print the value of height and depth variable.

C++

#include <bits/stdc++.h> using namespace std;  struct Node {     int data;     Node *left;     Node *right;     Node(int item)     {         data = item;         left = right = nullptr;     } };  void findDepthAndHeight(Node *root, int k) {     if (root == nullptr)         return;      int depth = -1;     int height = -1;     queue<Node *> q;     q.push(root);     int level = 0;      while (!q.empty())     {         int n = q.size();          for (int i = 0; i < n; i++)         {             Node *frontNode = q.front();              q.pop();              if (frontNode->data == k)             {                 depth = level;                                  // Clear the queue after finding the node                 while (!q.empty())                 {                     q.pop();                 }             }              // Push left and right children of              // the current node to the queue             if (frontNode->left)                 q.push(frontNode->left);             if (frontNode->right)                 q.push(frontNode->right);              if (frontNode->data == k)              {                 break;             }         }         // Increment the level after processing         // all nodes at the current level         level++;     }      height = level - depth - 1;     cout << "Depth : " << depth << endl;     cout << "Height : " << height << endl; }  int main() {     Node *root = new Node(5);     root->left = new Node(10);     root->right = new Node(15);     root->left->left = new Node(20);     root->left->right = new Node(25);     root->left->right->right = new Node(45);     root->right->left = new Node(30);     root->right->right = new Node(35);      int k = 10;      findDepthAndHeight(root, k);     return 0; }

Java

import java.util.LinkedList; import java.util.Queue;  class Node {     int data;     Node left, right;      Node(int item) {         data = item;         left = right = null;     } }  public class GfG{     static void findDepthAndHeight(Node root, int k) {         if (root == null) return;         int depth = -1;         int height = -1;         Queue<Node> q = new LinkedList<>();         q.add(root);         int level = 0;          while (!q.isEmpty()) {             int n = q.size();             for (int i = 0; i < n; i++) {                 Node frontNode = q.poll();                  if (frontNode.data == k) {                     depth = level;                     // Clear the queue after finding the node                     q.clear();                 }                  // Push left and right children of the current node to the queue                 if (frontNode.left != null) q.add(frontNode.left);                 if (frontNode.right != null) q.add(frontNode.right);                  if (frontNode.data == k) {                     break;                 }             }             // Increment the level after processing all nodes at the current level             level++;         }          height = level - depth - 1;         System.out.println("Depth : " + depth);         System.out.println("Height : " + height);     }      public static void main(String[] args) {         Node root = new Node(5);         root.left = new Node(10);         root.right = new Node(15);         root.left.left = new Node(20);         root.left.right = new Node(25);         root.left.right.right = new Node(45);         root.right.left = new Node(30);         root.right.right = new Node(35);          int k = 10;          findDepthAndHeight(root, k);     } }

Python

class Node:     def __init__(self, item):         self.data = item         self.left = None         self.right = None  def find_depth_and_height(root, k):     if root is None:         return     depth = -1     height = -1     q = [root]     level = 0      while q:         n = len(q)         for i in range(n):             front_node = q.pop(0)              if front_node.data == k:                 depth = level                 # Clear the queue after finding the node                 q.clear()              # Push left and right children of the current node to the queue             if front_node.left:                 q.append(front_node.left)             if front_node.right:                 q.append(front_node.right)              if front_node.data == k:                 break                      # Increment the level after processing all nodes at the current level         level += 1      height = level - depth - 1     print(f'Depth : {depth}')     print(f'Height : {height}')   def main():     root = Node(5)     root.left = Node(10)     root.right = Node(15)     root.left.left = Node(20)     root.left.right = Node(25)     root.left.right.right = Node(45)     root.right.left = Node(30)     root.right.right = Node(35)      k = 10      find_depth_and_height(root, k)   if __name__ == '__main__':     main()

using System; using System.Collections.Generic;  class Node {     public int data;     public Node left, right;      public Node(int item) {         data = item;         left = right = null;     } }  class GfG{     static void FindDepthAndHeight(Node root, int k) {         if (root == null) return;         int depth = -1;         int height = -1;         Queue<Node> q = new Queue<Node>();         q.Enqueue(root);         int level = 0;          while (q.Count > 0) {             int n = q.Count;             for (int i = 0; i < n; i++) {                 Node frontNode = q.Dequeue();                  if (frontNode.data == k) {                     depth = level;                     // Clear the queue after finding the node                     q.Clear();                 }                  // Push left and right children of the current node to the queue                 if (frontNode.left != null) q.Enqueue(frontNode.left);                 if (frontNode.right != null) q.Enqueue(frontNode.right);                  if (frontNode.data == k) {                     break;                 }             }             // Increment the level after processing all nodes at the current level             level++;         }          height = level - depth - 1;         Console.WriteLine("Depth : " + depth);         Console.WriteLine("Height : " + height);     }      static void Main() {         Node root = new Node(5);         root.left = new Node(10);         root.right = new Node(15);         root.left.left = new Node(20);         root.left.right = new Node(25);         root.left.right.right = new Node(45);         root.right.left = new Node(30);         root.right.right = new Node(35);          int k = 10;          FindDepthAndHeight(root, k);     } }

JavaScript

// Node structure class Node {     constructor(item) {         this.data = item;         this.left = null;         this.right = null;     } }  function findDepthAndHeight(root, k) {     if (root === null) return;     let depth = -1;     let height = -1;     let queue = [];     queue.push(root);     let level = 0;      while (queue.length > 0) {         let n = queue.length;         for (let i = 0; i < n; i++) {             let frontNode = queue.shift();              if (frontNode.data === k) {                 depth = level;                 // Clear the queue after finding the node                 queue = [];             }              // Push left and right children of the current node to the queue             if (frontNode.left) queue.push(frontNode.left);             if (frontNode.right) queue.push(frontNode.right);              if (frontNode.data === k) {                 break;             }         }         // Increment the level after processing all nodes at the current level         level++;     }      height = level - depth - 1;     console.log("Depth : " + depth);     console.log("Height : " + height); }  let root = new Node(5); root.left = new Node(10); root.right = new Node(15); root.left.left = new Node(20); root.left.right = new Node(25); root.left.right.right = new Node(45); root.right.left = new Node(30); root.right.right = new Node(35);  let k = 10;  findDepthAndHeight(root, k);

Output

Depth : 2 Height : 1

Time Complexity: O(n)
Auxiliary Space: O(n)due to queue data structure.

Count Balanced Binary Trees of Height h

mihikas

Improve

Article Tags :

Practice Tags :

Height and Depth of a node in a Binary Tree

[Approach 1] Using Recursion – O(n) time and O(h) space

[Approach 2] Using Level Order Traversal – O(n) time and O(n) space

Similar Reads