Finite Automata algorithm for Pattern Searching

Last Updated : 19 Jun, 2023

Given a text txt[0..n-1] and a pattern pat[0..m-1], write a function search(char pat[], char txt[]) that prints all occurrences of pat[] in txt[]. You may assume that n > m.
Examples:

Input:  txt[] = "THIS IS A TEST TEXT"         pat[] = "TEST" Output: Pattern found at index 10  Input:  txt[] =  "AABAACAADAABAABA"         pat[] =  "AABA" Output: Pattern found at index 0         Pattern found at index 9         Pattern found at index 12

Pattern

Pattern searching is an important problem in computer science. When we do search for a string in notepad/word file or browser or database, pattern searching algorithms are used to show the search results.

The string-matching automaton is a very useful tool which is used in string matching algorithm.
String matching algorithms build a finite automaton scans the text string T for all occurrences of the pattern P.

FINITE AUTOMATA

Idea of this approach is to build finite automata to scan text T for finding all occurrences of pattern P.
This approach examines each character of text exactly once to find the pattern. Thus it takes linear time for matching but preprocessing time may be large.
It is defined by tuple M = {Q, ?, q, F, d} Where Q = Set of States in finite automata

?=Sets of input symbols

q. = Initial state

F = Final State

? = Transition function

Time Complexity = O(M³|?|)

A finite automaton M is a 5-tuple (Q, q0,A,??), where

Q is a finite set of states,
q0 ? Q is the start state,
A ? Q is a notable set of accepting states,
? is a finite input alphabet,
? is a function from Q x ? into Q called the transition function of M.
The finite automaton starts in state q0 and reads the characters of its input string one at a time. If the automaton is in state q and reads input character a, it moves from state q to state ? (q, a). Whenever its current state q is a member of A, the machine M has accepted the string read so far. An input that is not allowed is rejected.

A finite automaton M induces a function ? called the called the final-state function, from ?* to Q such that ?(w) is the state M ends up in after scanning the string w. Thus, M accepts a string w if and only if ?(w) ? A.

Algorithm-

FINITE AUTOMATA (T, P) State <- 0 for l <- 1 to n State <- ?(State, ti) If State == m then Match Found end end

Why it is efficient?

These string matching automaton are very efficient because they examine each text character exactly once, taking constant time per text character. The matching time used is O(n) where n is the length of Text string.

But the preprocessing time i.e. the time taken to build the finite automaton can be large if ? is large.

Before we discuss Finite Automaton construction, let us take a look at the following Finite Automaton for pattern ACACAGA.

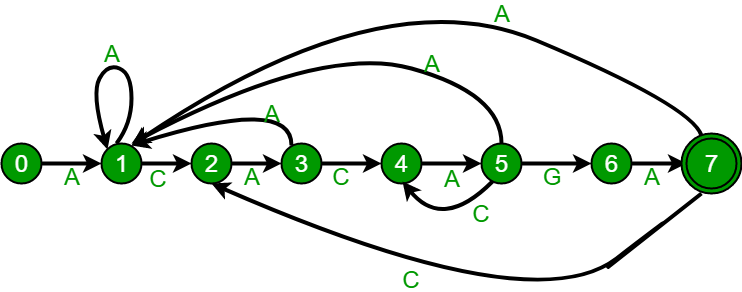
Finite Automata algorithm for Pattern Searching 1

Finite Automata algorithm for Pattern Searching 2

The above diagrams represent graphical and tabular representations of pattern ACACAGA.

Number of states in Finite Automaton will be M+1 where M is length of the pattern. The main thing to construct Finite Automaton is to get the next state from the current state for every possible character.

Given a character x and a state k, we can get the next state by considering the string "pat[0..k-1]x" which is basically concatenation of pattern characters pat[0], pat[1] ...pat[k-1] and the character x. The idea is to get length of the longest prefix of the given pattern such that the prefix is also suffix of "pat[0..k-1]x". The value of length gives us the next state.

For example, let us see how to get the next state from current state 5 and character 'C' in the above diagram. We need to consider the string, "pat[0..4]C" which is "ACACAC". The length of the longest prefix of the pattern such that the prefix is suffix of "ACACAC"is 4 ("ACAC"). So the next state (from state 5) is 4 for character 'C'.

In the following code, computeTF() constructs the Finite Automaton. The time complexity of the computeTF() is O(m^3*NO_OF_CHARS) where m is length of the pattern and NO_OF_CHARS is size of alphabet (total number of possible characters in pattern and text). The implementation tries all possible prefixes starting from the longest possible that can be a suffix of "pat[0..k-1]x". There are better implementations to construct Finite Automaton in O(m*NO_OF_CHARS) (Hint: we can use something like lps array construction in KMP algorithm).

We have covered the better implementation in our next post on pattern searching.

// C program for Finite Automata Pattern searching // Algorithm #include<stdio.h> #include<string.h> #define NO_OF_CHARS 256  int getNextState(char *pat, int M, int state, int x) {     // If the character c is same as next character     // in pattern,then simply increment state     if (state < M && x == pat[state])         return state+1;      // ns stores the result which is next state     int ns, i;      // ns finally contains the longest prefix     // which is also suffix in "pat[0..state-1]c"      // Start from the largest possible value     // and stop when you find a prefix which     // is also suffix     for (ns = state; ns > 0; ns--)     {         if (pat[ns-1] == x)         {             for (i = 0; i < ns-1; i++)                 if (pat[i] != pat[state-ns+1+i])                     break;             if (i == ns-1)                 return ns;         }     }      return 0; }  /* This function builds the TF table which represents4     Finite Automata for a given pattern */ void computeTF(char *pat, int M, int TF[][NO_OF_CHARS]) {     int state, x;     for (state = 0; state <= M; ++state)         for (x = 0; x < NO_OF_CHARS; ++x)             TF[state][x] = getNextState(pat, M, state, x); }  /* Prints all occurrences of pat in txt */ void search(char *pat, char *txt) {     int M = strlen(pat);     int N = strlen(txt);      int TF[M+1][NO_OF_CHARS];      computeTF(pat, M, TF);      // Process txt over FA.     int i, state=0;     for (i = 0; i < N; i++)     {         state = TF[state][txt[i]];         if (state == M)             printf ("\n Pattern found at index %d",                                            i-M+1);     } }  // Driver program to test above function int main() {     char *txt = "AABAACAADAABAAABAA";     char *pat = "AABA";     search(pat, txt);     return 0; }

CPP

// CPP program for Finite Automata Pattern searching  // Algorithm  #include <bits/stdc++.h> using namespace std; #define NO_OF_CHARS 256   int getNextState(string pat, int M, int state, int x)  {      // If the character c is same as next character      // in pattern,then simply increment state      if (state < M && x == pat[state])          return state+1;       // ns stores the result which is next state      int ns, i;       // ns finally contains the longest prefix      // which is also suffix in "pat[0..state-1]c"       // Start from the largest possible value      // and stop when you find a prefix which      // is also suffix      for (ns = state; ns > 0; ns--)      {          if (pat[ns-1] == x)          {              for (i = 0; i < ns-1; i++)                  if (pat[i] != pat[state-ns+1+i])                      break;              if (i == ns-1)                  return ns;          }      }       return 0;  }   /* This function builds the TF table which represents4      Finite Automata for a given pattern */ void computeTF(string pat, int M, int TF[][NO_OF_CHARS])  {      int state, x;      for (state = 0; state <= M; ++state)          for (x = 0; x < NO_OF_CHARS; ++x)              TF[state][x] = getNextState(pat, M, state, x);  }   /* Prints all occurrences of pat in txt */ void search(string pat, string txt)  {      int M = pat.size();      int N = txt.size();       int TF[M+1][NO_OF_CHARS];       computeTF(pat, M, TF);       // Process txt over FA.      int i, state=0;      for (i = 0; i < N; i++)      {          state = TF[state][txt[i]];          if (state == M)              cout<<" Pattern found at index "<< i-M+1<<endl;      }  }   // Driver program to test above function  int main()  {      string txt = "AABAACAADAABAAABAA";      string pat = "AABA";      search(pat, txt);      return 0;  }   //This code is contributed by rathbhupendra

Java

// Java program for Finite Automata Pattern // searching Algorithm class GFG {          static int NO_OF_CHARS = 256;     static int getNextState(char[] pat, int M,                                int state, int x)     {                  // If the character c is same as next         // character in pattern,then simply          // increment state         if(state < M && x == pat[state])             return state + 1;                      // ns stores the result which is next state         int ns, i;          // ns finally contains the longest prefix         // which is also suffix in "pat[0..state-1]c"          // Start from the largest possible value         // and stop when you find a prefix which         // is also suffix         for (ns = state; ns > 0; ns--)         {             if (pat[ns-1] == x)             {                 for (i = 0; i < ns-1; i++)                     if (pat[i] != pat[state-ns+1+i])                         break;                     if (i == ns-1)                         return ns;             }         }              return 0;     }      /* This function builds the TF table which     represents Finite Automata for a given pattern */     static void computeTF(char[] pat, int M, int TF[][])     {         int state, x;         for (state = 0; state <= M; ++state)             for (x = 0; x < NO_OF_CHARS; ++x)                 TF[state][x] = getNextState(pat, M, state, x);     }      /* Prints all occurrences of pat in txt */     static void search(char[] pat, char[] txt)     {         int M = pat.length;         int N = txt.length;          int[][] TF = new int[M+1][NO_OF_CHARS];          computeTF(pat, M, TF);          // Process txt over FA.         int i, state = 0;         for (i = 0; i < N; i++)         {             state = TF[state][txt[i]];             if (state == M)                 System.out.println("Pattern found "                           + "at index " + (i-M+1));         }     }      // Driver code     public static void main(String[] args)      {         char[] pat = "AABAACAADAABAAABAA".toCharArray();         char[] txt = "AABA".toCharArray();         search(txt,pat);     } }  // This code is contributed by debjitdbb.

Python3

# Python program for Finite Automata  # Pattern searching Algorithm  NO_OF_CHARS = 256  def getNextState(pat, M, state, x):     '''     calculate the next state      '''      # If the character c is same as next character        # in pattern, then simply increment state      if state < M and x == ord(pat[state]):         return state+1      i=0     # ns stores the result which is next state      # ns finally contains the longest prefix       # which is also suffix in "pat[0..state-1]c"       # Start from the largest possible value and        # stop when you find a prefix which is also suffix     for ns in range(state,0,-1):         if ord(pat[ns-1]) == x:             while(i<ns-1):                 if pat[i] != pat[state-ns+1+i]:                     break                 i+=1             if i == ns-1:                 return ns      return 0  def computeTF(pat, M):     '''     This function builds the TF table which      represents Finite Automata for a given pattern     '''     global NO_OF_CHARS      TF = [[0 for i in range(NO_OF_CHARS)]\           for _ in range(M+1)]      for state in range(M+1):         for x in range(NO_OF_CHARS):             z = getNextState(pat, M, state, x)             TF[state][x] = z      return TF  def search(pat, txt):     '''     Prints all occurrences of pat in txt     '''     global NO_OF_CHARS     M = len(pat)     N = len(txt)     TF = computeTF(pat, M)          # Process txt over FA.     state=0     for i in range(N):         state = TF[state][ord(txt[i])]         if state == M:             print("Pattern found at index: {}".\                    format(i-M+1))  # Driver program to test above function             def main():     txt = "AABAACAADAABAAABAA"     pat = "AABA"     search(pat, txt)  if __name__ == '__main__':     main()  # This code is contributed by Atul Kumar

// C# program for Finite Automata Pattern  // searching Algorithm  using System;  class GFG {  public static int NO_OF_CHARS = 256; public static int getNextState(char[] pat, int M,                                 int state, int x) {      // If the character c is same as next      // character in pattern,then simply      // increment state      if (state < M && (char)x == pat[state])     {         return state + 1;     }      // ns stores the result      // which is next state      int ns, i;      // ns finally contains the longest      // prefix which is also suffix in      // "pat[0..state-1]c"       // Start from the largest possible       // value and stop when you find a      // prefix which is also suffix      for (ns = state; ns > 0; ns--)     {         if (pat[ns - 1] == (char)x)         {             for (i = 0; i < ns - 1; i++)             {                 if (pat[i] != pat[state - ns + 1 + i])                 {                     break;                 }             }                 if (i == ns - 1)                 {                     return ns;                 }         }     }          return 0; }  /* This function builds the TF table which  represents Finite Automata for a given pattern */ public static void computeTF(char[] pat,                               int M, int[][] TF) {     int state, x;     for (state = 0; state <= M; ++state)     {         for (x = 0; x < NO_OF_CHARS; ++x)         {             TF[state][x] = getNextState(pat, M,                                          state, x);         }     } }  /* Prints all occurrences of     pat in txt */ public static void search(char[] pat,                            char[] txt) {     int M = pat.Length;     int N = txt.Length;       int[][] TF = RectangularArrays.ReturnRectangularIntArray(M + 1,                                                        NO_OF_CHARS);      computeTF(pat, M, TF);      // Process txt over FA.      int i, state = 0;     for (i = 0; i < N; i++)     {         state = TF[state][txt[i]];         if (state == M)         {             Console.WriteLine("Pattern found " +                                "at index " + (i - M + 1));         }     } }  public static class RectangularArrays { public static int[][] ReturnRectangularIntArray(int size1,                                                  int size2) {     int[][] newArray = new int[size1][];     for (int array1 = 0; array1 < size1; array1++)     {         newArray[array1] = new int[size2];     }      return newArray; } }   // Driver code  public static void Main(string[] args) {     char[] pat = "AABAACAADAABAAABAA".ToCharArray();     char[] txt = "AABA".ToCharArray();     search(txt,pat); } }  // This code is contributed by Shrikant13

JavaScript

<script> // Javascript program for Finite Automata Pattern // searching Algorithm  let NO_OF_CHARS = 256;  function getNextState(pat,M,state,x) {         // If the character c is same as next         // character in pattern,then simply          // increment state         if(state < M && x == pat[state].charCodeAt(0))             return state + 1;                        // ns stores the result which is next state         let ns, i;            // ns finally contains the longest prefix         // which is also suffix in "pat[0..state-1]c"            // Start from the largest possible value         // and stop when you find a prefix which         // is also suffix         for (ns = state; ns > 0; ns--)         {             if (pat[ns-1].charCodeAt(0) == x)             {                 for (i = 0; i < ns-1; i++)                     if (pat[i] != pat[state-ns+1+i])                         break;                     if (i == ns-1)                         return ns;             }         }                return 0; }  /* This function builds the TF table which     represents Finite Automata for a given pattern */ function computeTF(pat,M,TF) {     let state, x;         for (state = 0; state <= M; ++state)             for (x = 0; x < NO_OF_CHARS; ++x)                 TF[state][x] = getNextState(pat, M, state, x);     }  /* Prints all occurrences of pat in txt */ function search(pat,txt) {     let M = pat.length;         let N = txt.length;            let TF = new Array(M+1);         for(let i=0;i<M+1;i++)         {             TF[i]=new Array(NO_OF_CHARS);             for(let j=0;j<NO_OF_CHARS;j++)                 TF[i][j]=0;         }            computeTF(pat, M, TF);            // Process txt over FA.         let i, state = 0;         for (i = 0; i < N; i++)         {             state = TF[state][txt[i].charCodeAt(0)];             if (state == M)                 document.write("Pattern found " + "at index " + (i-M+1)+"<br>");         } }  // Driver code let pat = "AABAACAADAABAAABAA".split(""); let txt = "AABA".split("");  search(txt,pat);   // This code is contributed by avanitrachhadiya2155 </script>

Output:

  Pattern found at index 0   Pattern found at index 9   Pattern found at index 13

Time Complexity: O(m²)
Auxiliary Space: O(m)

References:
Introduction to Algorithms by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein

Boyer Moore Algorithm for Pattern Searching

kartik

Improve

Article Tags :

Practice Tags :

Pattern Searching

Finite Automata algorithm for Pattern Searching

Algorithm-

Similar Reads