Find the largest Complete Subtree in a given Binary Tree
Last Updated : 06 Jan, 2025
Given a Binary Tree, the task is to find the size and also the inorder traversal of the largest Complete sub-tree in the given Binary Tree.
Complete Binary Tree – A Binary tree is a Complete Binary Tree if all levels are filled except possibly the last level and the last level has all keys as left as possible.
Note: All Perfect Binary Trees are Complete Binary trees but the reverse is not true. If a tree is not complete then it is also not a Perfect Binary Tree.
Examples:
Input:
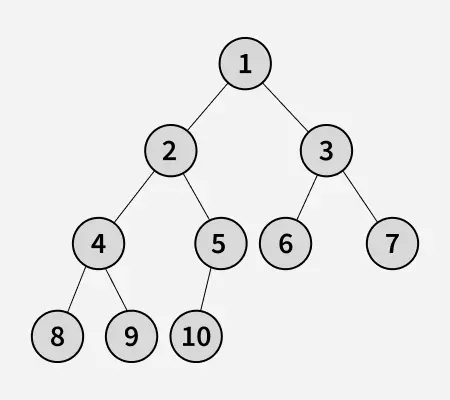
Output:
10
8 4 9 2 10 5 1 6 3 7
Explanation: The given tree as a whole is itself a Complete Binary Tree.
Input:
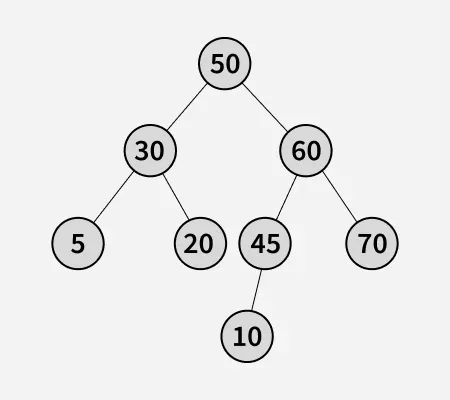
Output:
4
10 45 60 70
Explanation: The below subtree is the largest subtree that satisfies the conditions of a Complete Binary Tree
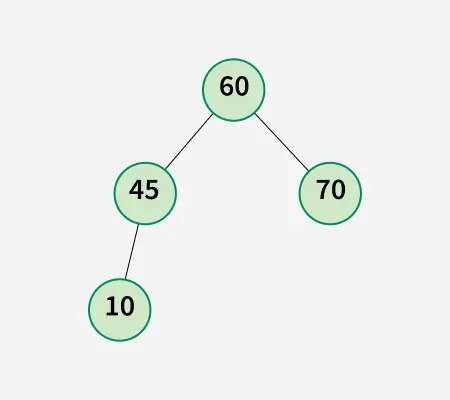
Approach:
The idea is to simply traverse the tree in a bottom-up manner. During the recursion, as the process moves from the child nodes back to the parent, the sub-tree information is passed up to the parent node. This information allows the parent node to perform the Complete Tree test in constant time. Both the left and right sub-trees pass details about whether they are Perfect or Complete, along with the maximum size of the largest complete binary sub-tree found so far.
To determine if the parent sub-tree is complete, the following three cases are evaluated:
- If the left sub-tree is Perfect and the right sub-tree is Complete, and their heights are equal, then the current sub-tree (rooted at the parent) is a Complete Binary Sub-tree. Its size is equal to the sum of the sizes of the left and right sub-trees plus one (for the root).
- If the left sub-tree is Complete and the right sub-tree is Perfect, and the height of the left sub-tree is greater than the height of the right sub-tree by one, then the current sub-tree (rooted at the parent) is a Complete Binary Sub-tree. Its size is again the sum of the sizes of the left and right sub-trees plus one (for the root). However, this sub-tree cannot be Perfect, because in this case, its left child is not perfect.
- If neither of the above conditions is satisfied, the current sub-tree cannot be a Complete Binary Tree. In this case, the maximum size of a complete binary sub-tree found so far in either the left or right sub-tree is returned. Additionally, if the current sub-tree is not complete, it cannot be perfect either.
C++ // C++ program to find the largest Complete // subtree of the given Binary Tree #include <bits/stdc++.h> using namespace std; class Node { public: int data; Node *left; Node *right; Node(int x) { data = x; left = nullptr; right = nullptr; } }; // Class to store details about the subtree class SubtreeInfo { public: // To store if the subtree is perfect bool isPerfect; // To store if the subtree is complete bool isComplete; // Size of the subtree int size; // Root of the largest complete subtree Node *rootTree; }; // Helper function to calculate height // from the size of the subtree int getHeight(int size) { // Height is calculated using the // formula for a perfect binary tree return ceil(log2(size + 1)); } // Function to find the largest complete binary subtree SubtreeInfo findCompleteBinaryTree(Node *root) { // Initialize the current subtree info SubtreeInfo currTree; // Base case: If the tree is empty if (root == nullptr) { currTree.isPerfect = true; currTree.isComplete = true; currTree.size = 0; currTree.rootTree = nullptr; return currTree; } // Recursive calls for left and right children SubtreeInfo leftTree = findCompleteBinaryTree(root->left); SubtreeInfo rightTree = findCompleteBinaryTree(root->right); // CASE - 1 // If the left subtree is perfect, the right // is complete, and their heights are equal, // this subtree is complete if (leftTree.isPerfect && rightTree.isComplete && getHeight(leftTree.size) == getHeight(rightTree.size)) { currTree.isComplete = true; currTree.isPerfect = rightTree.isPerfect; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 2 // If the left subtree is complete, the right // is perfect, and the height of the left is // greater by one, this subtree is complete if (leftTree.isComplete && rightTree.isPerfect && getHeight(leftTree.size) == getHeight(rightTree.size) + 1) { currTree.isComplete = true; currTree.isPerfect = false; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 3 // Otherwise, this subtree is neither perfect // nor complete. Return the largest subtree currTree.isPerfect = false; currTree.isComplete = false; currTree.size = max(leftTree.size, rightTree.size); currTree.rootTree = (leftTree.size > rightTree.size ? leftTree.rootTree : rightTree.rootTree); return currTree; } void inorderPrint(Node *root) { if (root != nullptr) { inorderPrint(root->left); cout << root->data << " "; inorderPrint(root->right); } } int main() { // Hardcoded given Binary Tree // 50 // / \ // 30 60 // / \ / \ // 5 20 45 70 // / // 10 Node *root = new Node(50); root->left = new Node(30); root->right = new Node(60); root->left->left = new Node(5); root->left->right = new Node(20); root->right->left = new Node(45); root->right->right = new Node(70); root->right->left->left = new Node(10); SubtreeInfo ans = findCompleteBinaryTree(root); cout << ans.size << endl; inorderPrint(ans.rootTree); return 0; } // Java program to find the largest Complete // subtree of the given Binary Tree import java.util.*; class Node { int data; Node left; Node right; Node(int x) { data = x; left = null; right = null; } } class SubtreeInfo { // To store if the subtree is perfect boolean isPerfect; // To store if the subtree is complete boolean isComplete; // Size of the subtree int size; // Root of the largest complete subtree Node rootTree; } class GfG { // Helper function to calculate height // from the size of the subtree static int getHeight(int size) { // Height is calculated using the // formula for a perfect binary tree return (int)Math.ceil(Math.log(size + 1) / Math.log(2)); } // Function to find the largest complete binary subtree static SubtreeInfo findCompleteBinaryTree(Node root) { // Initialize the current subtree info SubtreeInfo currTree = new SubtreeInfo(); // Base case: If the tree is empty if (root == null) { currTree.isPerfect = true; currTree.isComplete = true; currTree.size = 0; currTree.rootTree = null; return currTree; } // Recursive calls for left and right children SubtreeInfo leftTree = findCompleteBinaryTree(root.left); SubtreeInfo rightTree = findCompleteBinaryTree(root.right); // CASE - 1 // If the left subtree is perfect, the right // is complete, and their heights are equal, // this subtree is complete if (leftTree.isPerfect && rightTree.isComplete && getHeight(leftTree.size) == getHeight(rightTree.size)) { currTree.isComplete = true; currTree.isPerfect = rightTree.isPerfect; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 2 // If the left subtree is complete, the right // is perfect, and the height of the left is // greater by one, this subtree is complete if (leftTree.isComplete && rightTree.isPerfect && getHeight(leftTree.size) == getHeight(rightTree.size) + 1) { currTree.isComplete = true; currTree.isPerfect = false; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 3 // Otherwise, this subtree is neither perfect // nor complete. Return the largest subtree currTree.isPerfect = false; currTree.isComplete = false; currTree.size = Math.max(leftTree.size, rightTree.size); currTree.rootTree = (leftTree.size > rightTree.size ? leftTree.rootTree : rightTree.rootTree); return currTree; } static void inorderPrint(Node root) { if (root != null) { inorderPrint(root.left); System.out.print(root.data + " "); inorderPrint(root.right); } } public static void main(String[] args) { // Hardcoded given Binary Tree // 50 // / \ // 30 60 // / \ / \ // 5 20 45 70 // / // 10 Node root = new Node(50); root.left = new Node(30); root.right = new Node(60); root.left.left = new Node(5); root.left.right = new Node(20); root.right.left = new Node(45); root.right.right = new Node(70); root.right.left.left = new Node(10); SubtreeInfo ans = findCompleteBinaryTree(root); System.out.println(ans.size); inorderPrint(ans.rootTree); } } # Python program to find the largest Complete # subtree of the given Binary Tree import math class Node: def __init__(self, x): self.data = x self.left = None self.right = None class SubtreeInfo: # Initialize the subtree info def __init__(self): self.isPerfect = False self.isComplete = False self.size = 0 self.rootTree = None # Helper function to calculate height # from the size of the subtree def getHeight(size): # Height is calculated using the # formula for a perfect binary tree return math.ceil(math.log2(size + 1)) # Function to find the largest complete binary subtree def findCompleteBinaryTree(root): # Initialize the current subtree info currTree = SubtreeInfo() # Base case: If the tree is empty if root is None: currTree.isPerfect = True currTree.isComplete = True currTree.size = 0 currTree.rootTree = None return currTree # Recursive calls for left and right children leftTree = findCompleteBinaryTree(root.left) rightTree = findCompleteBinaryTree(root.right) # CASE - 1 # If the left subtree is perfect, the right # is complete, and their heights are equal, # this subtree is complete if (leftTree.isPerfect and rightTree.isComplete and getHeight(leftTree.size) == getHeight(rightTree.size)): currTree.isComplete = True currTree.isPerfect = rightTree.isPerfect currTree.size = leftTree.size + rightTree.size + 1 currTree.rootTree = root return currTree # CASE - 2 # If the left subtree is complete, the right # is perfect, and the height of the left is # greater by one, this subtree is complete if (leftTree.isComplete and rightTree.isPerfect and getHeight(leftTree.size) == getHeight(rightTree.size) + 1): currTree.isComplete = True currTree.isPerfect = False currTree.size = leftTree.size + rightTree.size + 1 currTree.rootTree = root return currTree # CASE - 3 # Otherwise, this subtree is neither perfect # nor complete. Return the largest subtree currTree.isPerfect = False currTree.isComplete = False currTree.size = max(leftTree.size, rightTree.size) currTree.rootTree = (leftTree.rootTree if leftTree.size > rightTree.size else rightTree.rootTree) return currTree def inorderPrint(root): if root is not None: inorderPrint(root.left) print(root.data, end=" ") inorderPrint(root.right) if __name__ == "__main__": # Hardcoded given Binary Tree # 50 # / \ # 30 60 # / \ / \ # 5 20 45 70 # / # 10 root = Node(50) root.left = Node(30) root.right = Node(60) root.left.left = Node(5) root.left.right = Node(20) root.right.left = Node(45) root.right.right = Node(70) root.right.left.left = Node(10) ans = findCompleteBinaryTree(root) print(ans.size) inorderPrint(ans.rootTree)
// C# program to find the largest Complete // subtree of the given Binary Tree using System; class Node { public int data; public Node left; public Node right; public Node(int x) { data = x; left = null; right = null; } } // Class to store details about the subtree class SubtreeInfo { // To store if the subtree is perfect public bool isPerfect; // To store if the subtree is complete public bool isComplete; // Size of the subtree public int size; // Root of the largest complete subtree public Node rootTree; } class GfG { static int GetHeight(int size) { // Height is calculated using the formula for a // perfect binary tree return (int)Math.Ceiling(Math.Log(size + 1) / Math.Log(2)); } // Function to find the largest complete binary subtree static SubtreeInfo FindCompleteBinaryTree(Node root) { // Initialize the current subtree info SubtreeInfo currTree = new SubtreeInfo(); // Base case: If the tree is empty if (root == null) { currTree.isPerfect = true; currTree.isComplete = true; currTree.size = 0; currTree.rootTree = null; return currTree; } // Recursive calls for left and right children SubtreeInfo leftTree = FindCompleteBinaryTree(root.left); SubtreeInfo rightTree = FindCompleteBinaryTree(root.right); // CASE - 1 // If the left subtree is perfect, the right // is complete, and their heights are equal, // this subtree is complete if (leftTree.isPerfect && rightTree.isComplete && GetHeight(leftTree.size) == GetHeight(rightTree.size)) { currTree.isComplete = true; currTree.isPerfect = rightTree.isPerfect; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 2 // If the left subtree is complete, the right // is perfect, and the height of the left is // greater by one, this subtree is complete if (leftTree.isComplete && rightTree.isPerfect && GetHeight(leftTree.size) == GetHeight(rightTree.size) + 1) { currTree.isComplete = true; currTree.isPerfect = false; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 3 // Otherwise, this subtree is neither perfect // nor complete. Return the largest subtree currTree.isPerfect = false; currTree.isComplete = false; currTree.size = Math.Max(leftTree.size, rightTree.size); currTree.rootTree = (leftTree.size > rightTree.size ? leftTree.rootTree : rightTree.rootTree); return currTree; } static void InorderPrint(Node root) { if (root != null) { InorderPrint(root.left); Console.Write(root.data + " "); InorderPrint(root.right); } } static void Main(string[] args) { // Hardcoded given Binary Tree // 50 // / \ // 30 60 // / \ / \ // 5 20 45 70 // / // 10 Node root = new Node(50); root.left = new Node(30); root.right = new Node(60); root.left.left = new Node(5); root.left.right = new Node(20); root.right.left = new Node(45); root.right.right = new Node(70); root.right.left.left = new Node(10); SubtreeInfo ans = FindCompleteBinaryTree(root); Console.WriteLine(ans.size); InorderPrint(ans.rootTree); } } // JavaScript program to find the largest Complete // subtree of the given Binary Tree class Node { constructor(x) { this.data = x; this.left = null; this.right = null; } } class SubtreeInfo { constructor() { // To store if the subtree is perfect this.isPerfect = false; // To store if the subtree is complete this.isComplete = false; // Size of the subtree this.size = 0; // Root of the largest complete subtree this.rootTree = null; } } // Helper function to calculate height // from the size of the subtree function getHeight(size) { // Height is calculated using the // formula for a perfect binary tree return Math.ceil(Math.log2(size + 1)); } // Function to find the largest complete binary subtree function findCompleteBinaryTree(root) { // Initialize the current subtree info let currTree = new SubtreeInfo(); // Base case: If the tree is empty if (root === null) { currTree.isPerfect = true; currTree.isComplete = true; currTree.size = 0; currTree.rootTree = null; return currTree; } // Recursive calls for left and right children let leftTree = findCompleteBinaryTree(root.left); let rightTree = findCompleteBinaryTree(root.right); // CASE - 1 // If the left subtree is perfect, the right // is complete, and their heights are equal, // this subtree is complete if (leftTree.isPerfect && rightTree.isComplete && getHeight(leftTree.size) === getHeight(rightTree.size)) { currTree.isComplete = true; currTree.isPerfect = rightTree.isPerfect; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 2 // If the left subtree is complete, the right // is perfect, and the height of the left is // greater by one, this subtree is complete if (leftTree.isComplete && rightTree.isPerfect && getHeight(leftTree.size) === getHeight(rightTree.size) + 1) { currTree.isComplete = true; currTree.isPerfect = false; currTree.size = leftTree.size + rightTree.size + 1; currTree.rootTree = root; return currTree; } // CASE - 3 // Otherwise, this subtree is neither perfect // nor complete. Return the largest subtree currTree.isPerfect = false; currTree.isComplete = false; currTree.size = Math.max(leftTree.size, rightTree.size); currTree.rootTree = leftTree.size > rightTree.size ? leftTree.rootTree : rightTree.rootTree; return currTree; } function inorderPrint(root) { let result = []; function inorder(node) { if (node !== null) { inorder(node.left); result.push(node.data); inorder(node.right); } } inorder(root); console.log(result.join(" ")); } // Hardcoded given Binary Tree // 50 // / \ // 30 60 // / \ / \ // 5 20 45 70 // / // 10 let root = new Node(50); root.left = new Node(30); root.right = new Node(60); root.left.left = new Node(5); root.left.right = new Node(20); root.right.left = new Node(45); root.right.right = new Node(70); root.right.left.left = new Node(10); let ans = findCompleteBinaryTree(root); console.log(ans.size); inorderPrint(ans.rootTree); Time Complexity: O(n), as each node is visited once in the recursion, where n is the total number of nodes in the tree.
Auxiliary Space: O(h), due to the size of the stack used for recursion
Similar Reads
Find the largest Perfect Subtree in a given Binary Tree
Given a Binary Tree, the task is to find the size of largest Perfect sub-tree in the given Binary Tree. Perfect Binary Tree - A Binary tree is Perfect Binary Tree in which all internal nodes have two children and all leaves are at the same level. Examples: Input: 1 / \ 2 3 / \ / 4 5 6 Output: Size :
12 min read
Find Kth largest number in a given Binary Tree
Given a Binary Tree consisting of n nodes and a positive integer k, the task is to find the kth largest number in the given tree.Examples: Input: k = 3 Output: 5Explanation: The third largest element in the given binary tree is 5. Input: k = 1 Output: 20Explanation: The first largest element in the
7 min read
Find LCA for K queries in Complete Binary Tree
Given an integer n. There is a complete binary tree with 2n - 1 nodes. The root of that tree is the node with the value 1, and every node with a value x has two children where the left node has the value 2*x and the right node has the value 2*x + 1, you are given K queries of type (ai, bi), and the
6 min read
Find the closest leaf in a Binary Tree
Given a Binary Tree and a key 'k', find distance of the closest leaf from 'k'. Examples: A / \ B C / \ E F / \ G H / \ / I J K Closest leaf to 'H' is 'K', so distance is 1 for 'H' Closest leaf to 'C' is 'B', so distance is 2 for 'C' Closest leaf to 'E' is either 'I' or 'J', so distance is 2 for 'E'
14 min read
Find largest subtree sum in a tree
Given a Binary Tree, the task is to find a subtree with the maximum sum in the tree. Examples: Input: Output: 28Explanation: As all the tree elements are positive, the largest subtree sum is equal to sum of all tree elements. Input: Output: 7Explanation: Subtree with largest sum is: Table of Content
15+ min read
Size of the Largest Trees in a Forest formed by the given Graph
Given an undirected acyclic graph having N nodes and M edges, the task is to find the size of the largest tree in the forest formed by the graph. A forest is a collection of disjoint trees. In other words, we can also say that forest is a collection of an acyclic graph which is not connected. Exampl
8 min read
Find the maximum element of every subtree of a Binary Tree
Given a Binary Tree, find the maximum element of every subtree of it. Examples :Input : 1 / \ 2 3 / \ / \ 4 5 6 7 Output : [4, 5, 5, 7, 6, 7, 7] Explanation: The maximum element of the subtree rooted at node 4 is 4. The maximum element of the subtree rooted at node 2 is 5. The maximum element of the
15+ min read
Find the level with maximum setbit count in given Binary Tree
Given a binary tree having N nodes, the task is to find the level having the maximum number of setbits. Note: If two levels have same number of setbits print the one which has less no of nodes. If nodes are equal print the first level from top to bottom Examples: Input: 2 / \ 5 3 / \6 1Output: 2Expl
11 min read
Find the maximum node at a given level in a binary tree
Given a Binary Tree and a Level. The task is to find the node with the maximum value at that given level. The idea is to traverse the tree along depth recursively and return the nodes once the required level is reached and then return the maximum of left and right subtrees for each subsequent call.
13 min read
Longest consecutive sequence in Binary tree
Given a Binary Tree find the length of the longest path which comprises of nodes with consecutive values in increasing order. Every node is considered as a path of length 1.Examples: In below diagram binary tree with longest consecutive path(LCP) are shown : Recommended PracticeLongest consecutive s
7 min read