Equation of Motion by Graphical Method
Last Updated : 02 Apr, 2024
A famous British scientist Isaac Newton derived three equations of motion that describe the most fundamental concepts of motion of an object. These equations govern the motion of an object in one, two, and three dimensions. These equations are easily used to calculate the values or the expressions for the position, velocity, or acceleration of an object at various times. Let's first understand the basic concept of motion and different terms related to it.
What is Motion?
Motion can be described as a change in the position of the object with respect to time. Position can be measured using a reference point and calculating the distance of the object from the reference point. Time can be calculated using a speed watch which will determine the time taken to change the position. There are many great scientists who worked and derived some equation or theory to study motion like Galileo Galilei and Isaac Newton.
 The motion of a car in a time interval
The motion of a car in a time intervalBefore discussing the equation of motion, let's first revise the basic terms related to the motion of an object. The motion of an object can be described using four different terms that are as follows:
Distance
The actual measure of the total change in the position of an object (in a particular time period) is called the Distance.
Distance (d) is a scalar quantity and hence, gives the magnitude only.
e.g. Consider the figure below, there is a car moving from position A to position B. The speedometer in the car will show the distance traveled from point A to point B.
 Distance traveled by car
Distance traveled by car
Displacement
The shortest measure of the net change in the position of an object (in a specific time interval) is called displacement.
Displacement is a vector quantity and hence, gives both a magnitude and the direction.
e.g. Consider the figure below, there is a car moving from position A to position B. The displacement is equal to the distance covered in a certain direction of the motion.
 Displacement of the car
Displacement of the car
Read More, Distance and Displacement
Speed
The speed of an object is the measure to determine how fast or slow the object move or changes its position.
Speed is equal to the time rate change in the distance covered by the object.
e.g. Suppose a fan which is running very fast, but it is fast with respect to your stationary state, if you will also spin at the same speed as the fan you will see it is not even moving.
Mathematically, the speed of an object is given as:
\text{Speed\, (s)}=\dfrac{\text{Distance (d)}}{\text{Time (t)}}
Since, both time and distance are scalar quantities therefore, speed is also a scalar quantity.
The SI unit of speed is m/s.
Velocity
The rate of change of displacement of an object with respect to time, or the rate of change of position, is called velocity.
Graphically, it is the slope of the displacement function. It is a vector quantity and thus gives both a magnitude and direction.
Mathematically, the velocity is defined as:
\text{Velocity (v)}=\dfrac{\text{Displacement (D)}}{\text{Time (t)}}
The SI unit of velocity is same as the speed that is, m/s. The difference between the speed and velocity of an object is that, the speed is a scalar quantity while the velocity is a vector quantity.
Acceleration
The change in velocity of an object per unit time, or the rate of change of velocity function with respect to time, is defined as the acceleration.
Graphically, it is the slope of the velocity function. Acceleration is a vector quantity and thus gives both a magnitude and direction.
Mathematically, the acceleration is defined as:
\text{Acceleration (a)}=\dfrac{\text{Velocity (v)}}{\text{Time (t)}}
What are the equations of motion?
The equations that explain the nature and the behavior of a physical system in terms of its motion as a function of time are called the equations of motion. There are three equations of motion that can be used to calculate the components of motion like distance, displacement, velocity (initial and final), time (t), and acceleration (a) of an object. The following are the three equation of motion:
- First Equation of Motion: v = u + at
- Second Equation of Motion: s = ut + 1/2(at2)
- Third Equation of Motion: v2 = u2 - 2as
where, v and u are the initial and the final velocities, a is the acceleration, t is the time taken and s is the displacement of an object.
Derivation of Equations of Motion
On the basis of the purpose of the application of different components in different solutions, there are three different ways to derive these equations:
- Derivation of the equations of motion algebraically, using the definition and different formulae of the components of the motion.
- Derivation of the equations of motion graphically, using the graphical representation for distance, velocity and acceleration of an object.
- Derivation of the equations of motion using integral method.
Here, in the present article, the derivation of the three equations of motion are discussed graphically as:
Derivation of First equation of motion graphically:
The first equation relates velocities with the acceleration and time of the object. Therefore, this equation is applicable when displacement is not given and so is also known as velocity-time relation.
Consider a velocity-time graph as shown below, the velocity of the body changes from A to C in time t at a uniform rate. The distance from A to the x-axis is the final velocity and OC is the total time t.
A perpendicular is drawn from B to OC, a parallel line is drawn from A to D, and another perpendicular is drawn from B to OE (represented by dotted lines).
The plot shows that the object has a variable velocity that is increasing from u to v as the slope is positive velocity is increasing in a positive direction.
 The velocity-time graph
The velocity-time graphNow we will calculate the acceleration using this motion graph. Acceleration is the tangent of the angle in v-t graph.
Acceleration = tan ∅ = \frac{AB}{CB} \\~\\ a = \frac{( v - u )}{t} \\~\\ rearrange\ above\ equation \\~\\ v = u + at\\
Derivation of Second equation of motion graphically:
Below v-t graph shows the velocity and time relationship of an object with an initial velocity of u m/s and final velocity of v m/s. As we know the area of the v-t graph gives the displacement of the object, so we will calculate the area of the graph and find out the equation of displacement. The same graph we have used in the previous derivation but here the approach will be different, earlier we used the slope to calculate acceleration, but now we will use area.
 v-t Motion Graph
v-t Motion GraphThe Displacement of the object (d) = Area of triangle ABC + Area of rectangle BCOT
Here, the area of the triangle ABC = 1/2 × Base × Height
= 1/2 × t × (v-u)
And the area of the rectangle BCOT = Length × Width
= u × t
Therefore, the displacement of the object, d = 1/2 × t × (v-u) + u × t ......(1)
Also, from the first equation of motion, v - u = at
Substitute at for v-u in the equation (1),
d = 1/2 × t × (at) + u × t
d = ut + (1/2)at2
Derivation of Third equation of motion graphically:
We have different ways to calculate areas, like dividing any form into small pieces and then adding up the area of converting the problem to a shape that is well known to us. In this derivation, the area of a rectangular shape is converted and the displacement is calculated using the area of a rectangle. This equation is used when time is not given.
 Original graph to highlighted graph
Original graph to highlighted graphHere, P is the Centre point, so the speed of the object is (v + u) / 2.
Therefore, the displacement of the object (d) = the area of the triangle ABC + the area of the rectangle ACTO = the area of the rectangle OPQT
The displacement of the object, d = Length × Width
= t × (v + u) / 2 ......(2)
Also, from the first equation of motion, v - u = at or t = (v - u) / a
Therefore, the equation (2) becomes:
d = (v - u) / a × (v + u) / 2
v2 = u2 - 2ad
Read More,
Sample Problems
Problem 1: Speed-time graph for a particle is given below, find the distance covered by the particle in 40 minutes.
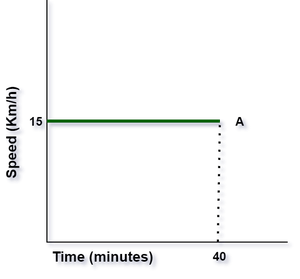 Speed-Time Plot
Speed-Time PlotSolution:
Calculating distance using the area under the speed-time graph.
 Area under the given curve.
Area under the given curve.Distance covered by the particle in 40 min = Area under the given curve.
The shape formed under the curve is of a rectangle therefore, the area under the curve = length × width.
Here, the length of the shape is equivalent to the time taken i.e. 40 min or 40 min × 60 s/1 min = 2400 s.
Similarly, the width of the shape is equivalent to the speed i.e. 15 km/h or 15 km/h × 1 h/3600 s × 1000 m/1 km = 4.17 m/s.
Therefore, the area under the curve or the distance covered in 40 min is given by:
⇒ 2400 s × 4.17 m/s = 10000 m or 10 km.
Hence, the distance covered by the particle in 40 min is equal to 10 km.
Problem 2: For the Below, graph calculates the distance covered by the particle between the time 20 minutes to 40 minutes.
 Speed-Time plot
Speed-Time plotSolution:
Distance covered by the particle from time t = 20 min to 40 min is equal to the Area under the given curve between the given time range.
 Highlighted Area of Speed-time Plot
Highlighted Area of Speed-time PlotThe shape formed under the curve is of a rectangle therefore, the area under the curve = length × width.
Here, the length of the shape is equivalent to the time taken i.e. (40 - 20) min or 20 min × 60 s/1 min = 1200 s.
Similarly, the width of the shape is equivalent to the speed i.e. 15 km/h or 15 km/h × 1 h/3600 s × 1000 m/1 km = 4.17 m/s.
Therefore, the area under the curve or the distance covered from time t = 20 min to 40 min is given by:
⇒ 1200 s × 4.17 m/s = 5004 m or 5.004 km.
Hence, the distance covered by the particle from time t = 20 min to 40 min is equal to 5.004 km.
Problem 3: Find the distance covered by a particle during the time interval t = 0 s and t = 4 s for which the speed-time graph is given below:
 Speed-time plot
Speed-time plotSolution:
 Speed-Time Graph
Speed-Time GraphDistance covered by the particle in t = 0 s and t = 4 s is equal to area under the curve.
The shape formed under the curve is of a triangle therefore, the area under the curve = 1/2 × base × height.
Here, the base of the shape is equivalent to the time taken i.e. 4 s.
Similarly, the height of the shape is equivalent to the speed i.e. 20 m/s.
Therefore, the area under the curve or the distance covered in t = 0 s and t = 4 s is given by:
⇒ 1/2 × 4 s × 20 m/s = 40 m.
Hence, the distance covered by the particle in t = 0 s and t = 4 s is equal 40 m.
Problem 4: The figure below shows the distance-time graph of three objects A, B, and C. Determine:
(a) which object is moving with a greater speed?
(b) which object is moving with a lesser speed?
 Distance-Time Plot
Distance-Time PlotSolution:
The given graph is distance time graph and the slope gives us the value of speed i.e. more the slope more is speed.
As it is observed from the given graph, A has maximum slope, so it is moving with greater speed and C has the least slope, so it is moving with the slowest speed.
Problem 5: Calculate the speed of the particle with the help of the given distance-time motion graph.
 Distance-Time Plot
Distance-Time PlotSolution:
Here, the speed of the particle is equal to the slope of the graph.
And the slope of the distance graph is equal to the speed of the particle.
Therefore, the formula to calculate the speed of the particle is:
Speed = Distance / Time
= 20 m / 5 s
= 4 m/s.
Hence, the speed of the particle is equal to 4 m/s.
Similar Reads
CBSE Class 9 Science Notes 2023-2024 CBSE Class 9 Science Notes for the academic year 2023-2024 serve as a crucial foundation for students' further education. To excel in exams, it is critical to fully comprehend each topic while also thoroughly revising the subject matter. As Class 9 is a crucial period for students, GeeksforGeeks pro
15+ min read
Chapter 1 - Matter in Our Surroundings
Matter is Made of Tiny ParticlesIn our surroundings, we come across different shapes, sizes, heights, structures, and textures. According to scientists everything in this universe is made up of a material called Matter. We can see that matter occupies some space and mass, in another way we can say that matter has some ‘volume’ and
8 min read
States of Matter: Solid, Liquid, Gas and PlasmaMatter is made up of tiny particles. These particles are such small that we cannot see them by the naked eye. What ever we see in nature is made up of matter. Different matter exist in different form. These forms are called states of matter. States of MatterState of Matter or Phases of Matter is def
9 min read
Change of State of MatterWhen cubes of ice melt into water or liquid boils into vapor, you may have seen changes in states of matter, but have you ever wondered why the substances change their form? When matter loses or gains energy, it changes its condition. When a substance gains energy, its molecules or atoms move faster
6 min read
EvaporationEvaporation occurs when a liquid turns into a gas. Have you ever noticed that when a glass is left on the counter, the water begins to evaporate? It's evaporation, not thirsty fairies dwelling in your kitchen. Evaporation is the process by which molecules undergo a spontaneous transition from the li
10 min read
Chapter 2 - Is Matter Around Us Pure
Chapter 3 - Atoms and Molecules
Laws of Chemical CombinationLaws of Chemical Combination are one of the most fundamental building blocks of the subject of chemistry. As in our surrounding different matter reacts with each other and form various kind of different substances. Laws of Chemical Combination are the collection of laws that explains how these subst
7 min read
What is Atom?Atoms are tiny particles that comprise all the things in the known universe. Atoms of an element are responsible for all chemical reactions occurring in nature. We know that atoms are made up of three fundamental particles namely, ElectronsProtonsNeutronsThese particles are also called subatomic par
8 min read
Difference Between Atom And MoleculeAtoms and Molecules are the basic building blocks of all matter around us. There are some fundamental differences between atoms and molecules but they are essential in understanding the behavior of the world around us. Initially, atoms were thought to be indestructible, i.e. we can not further break
6 min read
Chemical FormulaChemical formula is a way to describe chemical ratios of atoms that make up a specific chemical compound or molecule in chemistry. Chemical element symbols, numbers, and sometimes other symbols, such as parentheses, dashes, brackets, commas, plus (+), and minus (-) signs, are used to represent the c
6 min read
Molecular MassMolecular Mass is the mass of all the atoms present in a molecule. In ancient India and Greece, philosophers have first given the idea of atoms and deeply studied them. Around 500 BC.Everything around is made up of very small units these units are atoms in the language of science, very small in the
8 min read
Chapter 4 - Structure of the Atom
Chapter 5 - The Fundamental Unit of Life
What are Living Organisms Made Up of?Robert Hooke discovered the cells in the year 1665. He was examining a thin slice of a cork, he saw that the cork resembled the structure of a honeycomb with too many little compartments. Then with the microscope, he observed these compartments and called them cells, meaning "little room" in Latin.
7 min read
Plasma Membrane - Definition, Structure, Components, FunctionsThe plasma membrane acts as a protective barrier made of a lipid bilayer with embedded proteins that separates the interior of the cell from its external environment. The plasma membrane, also known as the cell membrane, is a vital component of the living organism that regulates the movement of subs
4 min read
Cell WallCell wall is the non-living material that protects a cell's outermost layer. It might be firm, elastic, or periodically rigid. It serves as a filtration system as well as structural support and protection for the cell. Cell walls are absent in many eukaryotes, including animals, but they are present
7 min read
Nucleus: Structure and FunctionThe nucleus (plural: nuclei) is a double-membraned organelle that is found only in eukaryotic cells. The name nucleus comes from a Latin term that means "nut kernel." The nucleus was discovered by Robert Brown in 1831. It is the first cell organelle that was discovered. The nucleus is responsible fo
7 min read
Cytoplasm - Structure and FunctionCytoplasm is a semi-fluid, gel-like substance found in all living cells, both prokaryotic and eukaryotic. It surrounds the cell's organelles and nucleus. It acts as the medium in which various cellular processes like protein synthesis, metabolism, and many chemical reactions take place. The cytoplas
6 min read
Endoplasmic Reticulum - Structure, Types And FunctionsEndoplasmic reticulum is an important cell organelle present in the cytoplasm of eukaryotic cells. The structure of the Endoplasmic reticulum comprises membranous tubules that are interconnected and carry out major cellular functions like protein synthesis, breakdown of carbohydrates, lipid synthesi
7 min read
Golgi ApparatusGolgi apparatus is an organelle found in most of the eukaryotes. It consists of a series of flattened membrane sacs called cisternae. These cisternae are present one over the other to form the Golgi complex. It is responsible for packaging proteins into vesicles before secretion and therefore plays
4 min read
Lysosomes - Definition, Types, Significance, FunctionsLysosomes are cell organelles that are also known as "suicide bags" or "cell recycling centers" of the cell. Lysosomes function in cellular waste disposal and programmed cell death (apoptosis). Lysosomes are eukaryotic membrane-bound cell organelles that appear small and spherical. Lysosomes arise f
8 min read
MitochondriaMitochondria is a double membrane organelle present in the cytoplasm of all eukaryotic cells. Mitochondria generates energy in the form of ATP because of which mitochondria is known as the "powerhouse of the cell". In 1857 Albert von Kolliker first discovered the organelle and Carl Benda in 1898 gav
7 min read
What are Plastids? - Class 9 BiologyThe body of all living organisms is made up of cells. Based on the cellular organization, some organisms are made up of single cells which are unicellular, and more than one cell which is multicellular organisms. Single-cell is able to perform all the life processes like gaining food, respiration, e
8 min read
VacuolesVacuole is a cellular organelle that is found in plants, fungi, and some types of protists. In plant cells, it helps in maintaining turgor pressure, contributing to the plant's structural support and rigidity. Vacuoles contain various substances like ions, water, and waste products. It also contribu
5 min read
Cell Division: Mitosis & Meiosis, Different Phases of Cell CycleCell division is the process by which a parent cell divides into two daughter cells. It occurs through two distinct processes, mitosis, and meiosis, each having its role in the life cycles of organisms. Mitosis is the division of a cell that produces two identical daughter cells, essential for growt
9 min read
Chapter 6 - Tissues
Meristematic Tissues - Definition, Features, Types, RoleMeristematic tissues are a type of plant tissue that plays an important role in the growth and development of plants. These tissues consist of undifferentiated cells that can divide and differentiate into various types of specialized cells. Meristematic tissues are mainly found in that part of the p
6 min read
Structure and Types of Animal TissuesAnimal tissue is a group of cells along with intercellular substances that perform one or more functions in the body. The structure of animal tissues depends on their function and location in the body. There are four types of animal tissues; epithelial, connective, muscle, and nervous tissue which w
6 min read
Permanent Tissues - Diagram, Types Notes Biology Class 9Permanent tissues are a type of plant tissue that has completed its growth and differentiation. They remain in a specialized state throughout the plant's life. These tissues perform specific functions and are responsible for the overall structural growth and function of the plant. There are three ma
7 min read
Epithelial Tissue - Introduction, Characteristics, Types, ImportanceEpithelial tissue is what makes up this part of the animal's anatomy, and it may be found on both the outside and the inside of the body. The body structure of multicellular organisms is more complicated than that of unicellular organisms, in which every important cellular function, such as nutritio
13 min read
Overview and Types of Connective TissueAs their name suggests, connective tissues serve to both support and link the many organs and tissues found throughout the body. They are located in vast quantities all throughout the body, Their genesis may be traced back to the mesoderm(embryo). A few cells that are located in the interfacial netw
13 min read
Muscular TissueMuscular tissue is a type of tissue present in animals that is specialized for contraction and movement. Muscular tissue is one of the four main types of tissues, the others being epithelial, connective, and nervous tissue. Muscular tissue is made up of muscle fibers. There are three types of muscul
5 min read
Nervous Tissue - Definition, Characteristics, Functions, TypesNervous tissue is one of the four types of animal tissue, along with epithelial tissue, connective tissue, and muscle tissue. Nervous tissue is composed of two main types of cells: neurons and glial cells. Nervous tissue is present in the brain, spinal cord, and nerves all around the body. Nervous t
6 min read
Chapter 7 - Motion
What is Motion?Motion is defined as the change in the position of an object with respect to time i.e. when an object changes its position according to time it is said to be in the state of motion. Everything in the universe is in a state of continuous motion, for example, the moon revolves around the planets, the
12 min read
Measuring the Rate of MotionWe use general things around us that are moving, like if we see around us, monitor air moving around us, like we have clocks with the hands moving, we all know that day and night is caused because of motion of Earth around the Sun, yet seasons are caused because of it. So we are going to study in de
10 min read
AccelerationAcceleration is defined as the rate of change in velocity. This implies that if an object’s velocity is increasing or decreasing, then the object is accelerating. Acceleration has both magnitude and direction, therefore it is a Vector quantity. According to Newton's Second Law of Motion, acceleratio
9 min read
Equation of Motion by Graphical MethodA famous British scientist Isaac Newton derived three equations of motion that describe the most fundamental concepts of motion of an object. These equations govern the motion of an object in one, two, and three dimensions. These equations are easily used to calculate the values or the expressions f
12 min read
Uniform Circular MotionUniform Circular Motion as the name suggests, is the motion of a moving object with constant speed in a circular path. As we know, motion in a plane only has two coordinates, either x, and y, y and z, or z and x. Except for Projectile motion, circular motion is also an example of motion in a 2-D pla
9 min read
Chapter 8 - Force and Laws of Motion
Balanced and Unbalanced ForcesForces are required to move, turn, shift, release, shut, drive, drag, and so on. When you throw a ball, you are exerting energy on it to propel it through the air. A push or pull is referred to as a force. Forces can cause objects to move, and they can also slow, stop, or change the direction in whi
8 min read
Newton's First Law of MotionBefore the revolutionary ideas of Galileo and Newton, people commonly believed that objects naturally slowed down over time because it was their inherent nature. This assumption stemmed from everyday observations, where things like friction, air resistance, and gravity seemed to slow moving objects.
15+ min read
Mass and InertiaMany events are seen in the field of physics, yet some of them have eluded explanation for a long time. Newton proposed three rules of motion, which became known as Newton's Laws of Motion. These laws were a novel finding in the physical universe, and they were frequently employed to explain situati
8 min read
Newton's Second Law of Motion: Definition, Formula, Derivation, and ApplicationsNewton's Second Law of Motion is a fundamental principle that explains how the velocity of an object changes when it is subjected to an external force. This law is important in understanding the relationship between an object's mass, the force applied to it, and its acceleration.Here, we will learn
15 min read
Newton's Third Law of MotionWhen you jump, you feel the gravitational force pulling you down towards the Earth. But did you know that at the same time, you are exerting an equal force on the Earth? This phenomenon is explained by Newton's Third Law of Motion. Newton's Third Law of MotionNewton's Third Law of Motion is a founda
13 min read
Chapter 9 - Gravitation
Gravitational ForceHave you ever wondered why the Earth revolves around the Sun and not the other way around? Or why does the Moon remain in orbit instead of crashing into Earth? If the Earth pulls the Moon and the Moon pulls the Earth, shouldn’t they just come together? What keeps them apart?All these questions can b
11 min read
Free FallThere are always two cases of things falling to the ground. One example is when something is thrown to the ground, such as throwing a ball. At the same time, the other case is when something is dropped to the ground. For example, dropping the ball or accidentally dropping the phone from your hands (
6 min read
Mass and WeightMass and Weight are commonly used in the same manner by the general masses but there are differences between both Mass and Weight, where Mass is the measure of Inertia unlike Weight which is a measure of force acting on a body towards the heavy body. But yet still many people use these two terms int
10 min read
What is Pressure?Have you ever thought about why a needle is so thin, why fence spikes are pointed, or why a hammer's head is flat? It’s all about pressure. Pressure is the force applied to a specific area. A needle’s sharp tip concentrates the force, allowing it to easily pierce fabric. If it were blunt, the force
7 min read
Archimedes PrincipleArchimedes Principle is a fundamental concept in fluid mechanics, credited to the ancient Greek mathematician and physicist Archimedes. According to Archimedes' Principle, when an object is immersed in a fluid the object experiences an upward force whose magnitude is equal to the weight of the fluid
12 min read