Electric field is a fundamental concept in physics, defining the influence that electric charges exert on their surroundings. This field has both direction and magnitude. It guides the movement of charged entities, impacting everything from the spark of static electricity to the functionality of electronic devices Understanding electric fields will help you to understand how charge particles interact with each other and the surroundings and guide various natural and technological phenomena. In this article, we will learn in detail about electric field, its formula, calculation of electric field for ring, straight wire and continuous charge distribution.
What is an Electric Field?
Electric Field is a fundamental concept in physics, they are a physical field that surrounds an electrically charged particle. Charged particles exert attractive force when they have opposite charges and repulsive force when they have the same charges in this field. The electric field of a single charge describes its power to exert such forces on another charged object.
The electric field is a vector quantity which means it has both magnitude and direction.
Mathematically electric field(E) is described at a given point is defined as the force (F) experienced by a test charge (q) placed at that point, divided by the magnitude of the test charge:
E = F/q
Direction Of Electric Field
The direction of electric field is taken as the direction of the force which is exerted on the positive charge. The electric field is radially outwards from the positive charge and radially inwards to the negative point charge, as shown in the picture given below:
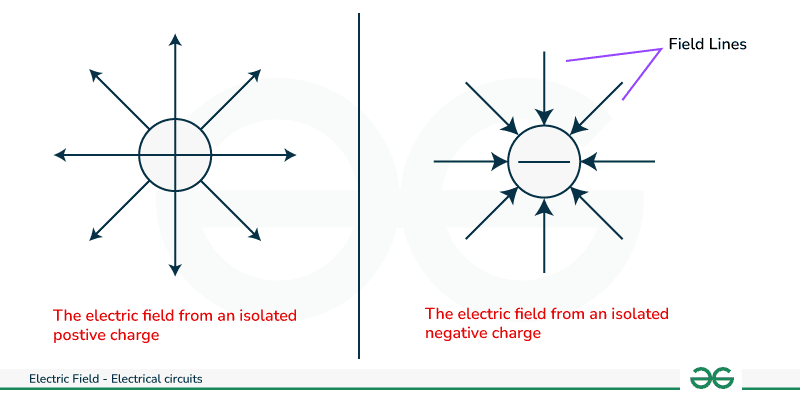Electric Field LinesNow, let us see some of the important terminologies related to electric field that will be discussed further in the article:
- Electric Charge: An electric charge is a property of matter that causes two objects to repel or attract. It can be either negative or positive.
- Point charge: When discussing a body considerably smaller than the distance being considered, we disregard its size and refer to it as a point charge.
- Coulomb's Law: Coulomb's law states that the force between two point charges is directly proportional to the magnitudes of the charges and inversely proportional to the distance between the two charges.
- Mathematically : F = (k|q1q2|)/r2 ,where q1=first point charge ,q2 = second point charge.
- k = 8.988 * 109 Nm2/C2 is Coulomb’s constant, r = the distance between two point charges.
- Gauss's law : Gauss’s law states that the net flux of an electric field in a closed surface is directly proportional to the enclosed electric charge.( further discussed in detail in the article).
- Electric flux: Electric flux is defined as the total number of electric field lines passing through a specified area within a unit of time.
Electric Field Lines
Electric field lines are imaginary lines used to depict the direction and strength of an electric field surrounding charged objects. They were introduced by the physicist Michael Faraday in the 19th century as a conceptual tool for understanding electric fields.
Properties of Electric Field Lines
Electric field lines have different properties. Some of the properties are provided below:
- Field lines never intersect each other.
- They are perpendicular to the surface charge.
- The strength of an electric field increases when the field lines are closer together, which indicates a stronger force. Conversely, when field lines move farther apart, the field weakens.
- The quantity of field lines directly proportional to the magnitude of the charge.
- These lines generally originate from positive charges and ends at negative charges, depicting the direction of the electric field.
Electric Field Calculation
Various methods are followed to calculate electric field are as followed:
Calculate Electric Field Using Coulomb's Law
According to Coulomb's law, a force with electric charge q1 at position x1 exerts a force on a particle with charge q2 at position x0 of ,(equation-1)
\vec F= \frac{1}{4\piε_0}\frac{Q.q}{r^2}\hat r
where
- \hat r is a unit vector in the direction from of electrostatic force
- ε0 is the electric constant, known as absolute permittivity of free space .
We know that electric field is given as force per unit test charge. Let q is the test charge. Hence, electric field is given as
\vec E = \frac {\vec F}{q} = \frac{1}{4\pi\varepsilon_0} \frac {Q}{r^2}\hat r
Calculate Electric Field Using Gauss's Law
Gauss's law states that the total flux linked with a closed surface is 1/ε0 times the charge enclosed by the closed surface. Hence, according to Gauss Law, electric field is given as follows:
∮ \overrightarrow{\rm E}.\overrightarrow{\rm ds}= \frac {q}{\varepsilon_0}
It is easy to calculate electric field using Gauss's law as compare to Coulomb's law. If we carefully observe, Gauss's law is a replica of Coulomb's law.
How to Find the Electric Field Using Gauss Law?
- Choose a Symmetrical Gaussian Surface: Select a closed surface where the electric field is constant in magnitude and direction. The symmetry can be spherical, cylindrical or planar depending upon the charge distribution.
- Determine the Enclosed Charge: Calculate the total charge enclosed in the chosen Gaussian surface.
- Calculate Electric Flux: Evaluate the flux of the electric field through the Gaussian surface
- Ultimately leads to finding the electric field using gauss law with the help of the formula given above.
Let's say you have a spherically symmetric charge distribution with total charge Q uniformly distributed within a sphere of radius R. Our aim is to find electric field at a distance r from the center:
- Choose a Gaussian Surface: A spherical Gaussian surface with radius r > R is suitable for this case.
- Determine Enclosed Charge: The enclosed charge is q for r ≤ R and Q for r > R (as whole body is enclosed).
- Calculate Electric Flux: The electric flux through the spherical surface is given as E × A, where E is the magnitude of the electric field and A is area
- Apply Gauss's Law: By Set up Gauss's law equation:
∮\overrightarrow{\rm E}.\overrightarrow{\rm dA} = \frac {q_{enclosed}}{\epsilon_0}
From Gauss Law
4πr2.E = Q/ε0
From this equation, you can solve for the magnitude of the electric field
E at a distance r from the center is given as
\vec E = \frac {1}{4\pi \epsilon_0} \frac {Q}{r^2}
This example illustrate how to use Gauss's law for a spherically symmetric charge distribution. See, the approach and the shape of the Gaussian surface can vary based on the symmetry of the charge distribution provided in the question.
Electric Field For Continuous Charge Distribution
Let us talk about the different types of charge distribution
- Linear Charge Distribution
- Surface Charge Distribution
- Volume Charge Distribution
Linear Charge Distribution
Linear charge distribution: If charge is distributed linearly over a body.
λ = dq/dl
- λ = linear charge density
- dq = charge
- dl = line element
Consider an infinitesimally small element of charge (dq) along the line, the electric field contribution (dE) from this element can be calculated using Coulomb's law: dE = k⋅dq/r2 where k is Coulomb's constant.
Integrate dE over the entire length of the line charge to obtain the total electric field E = ∫k⋅dq/r2
Surface Charge Distribution
Surface charge distribution: If charge is distributed continuously over the surface of a body
σ = dq/ds
- σ = surface charge density
- dq = charge
- ds = surface element
Consider an infinitesimally small element of charge (dq) on the surface, the electric field contribution (dE) from this element can be calculated using Coulomb's law: dE = k⋅dq/r2, where k is Coulomb's constant.
Integrate dE over the entire surface to obtain the total electric field E = ∫k⋅dq/r2
Volume Charge Distribution
Volume charge distribution: If charge is distributed continuously over the volume of a body.
ρ = dq/dv
- ρ = volume charge density
- dq = charge
- dv = volume element
Consider an infinitesimally small volume element containing charge (dV) within the region, the electric field contribution (dE) from this volume element can be calculated using Coulomb's law: dE = k⋅dq/r2, where dq = ρ⋅dV and k is Coulomb's constant.
Integrate dE over the entire volume to obtain the total electric field E = ∫k⋅dq/r2
Applications of Gauss Law to Find Electric Field
Now, let us see some of the application of gauss law to find electric field:
Electric Field due to a Line Charge
Suppose a line charge having linear charge density λ is given in the form of a thin charged rod.
Diagram for line charge To find the electric field intensity at point P along a wire, a cylindrical Gaussian surface is selected. This choice is made to apply Gauss's law for finding the electric field, E, at point P.
The electric flux passing through the end surfaces of the cylindrical Gaussian surface is ,that is Φ1 = 0.
And , the electric flux passing through the curved surface of the cylindrical Gaussian surface is given as:
Surface area of curved part is given as: S = 2πrl
Total charged enclosed by gaussian surface is q = λ × l
Surface area and charge of gaussian surface (Equation-5)
The electric flux through the curved surface of the cylindrical Gaussian surface is given as:
\phi = \overrightarrow{\rm E}.\overrightarrow{\rm dS}
Φ = E. cos θ.S = E × 1 × 2πrl
Total electric flux is given as:
Φ = Φ1 + Φ2
Φ = 0 + E.cos θ.S
Φ = E × 2πrl
From Gauss's law, we know that,
Φ = q/ε0 = λl/ε0
2πrl × E = λl/ε0
E = \frac {1}{2\pi\epsilon_0} \frac {\lambda}{r}
Electric Field Due to Ring
Now, let us take a look into the electric field due to Ring
For, Electric Field Intensity at Any Point on the Axis of a Uniformly Charged Ring, let us consider a wire forming a circular ring with negligible thickness and a radius of R, carrying a uniform charge +q distributed evenly around its circumference. Our aim is to calculate the electric field intensity at any point P along the axis of the loop, positioned at a distance x from the ring's center, marked as O.
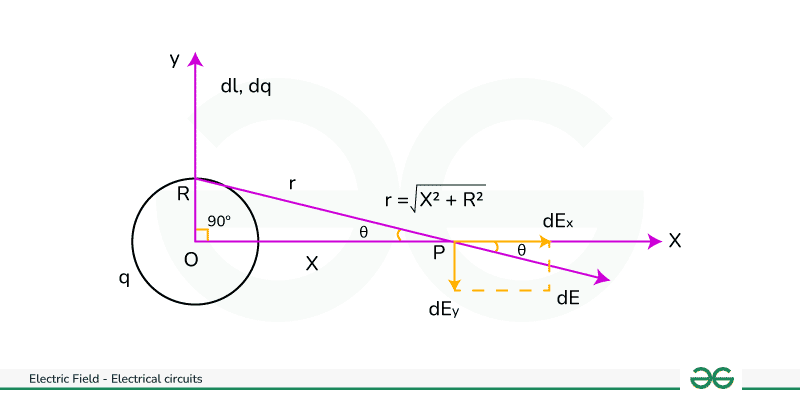Diagram showing electric field due to charged ringLet AB be the length of element dl.
The charge on the element AB is,
dq = (q × dl)/2πR
Electric field intensity at P due to charge element AB is,
|dE| = k dq/(CP)2
where, k = constant
|dE| = k dq/(R2 + x2)
Now, resolve the electric field intensity dE into two rectangular components, that is
dE sinθ along the y-axis and dE cosθ along the x-axis.
And for diametrically opposite elements of the charged ring, the perpendicular components of the electric field intensity will nullify each other, resulting in,
∫dE sinθ = 0.
Whereas components along the axis of the charged ring will undergo integration. That is, ∫dE cosθ.
Hence, the resultant electric field intensity E at P is | E | = ∫dE cosθ
In △OPC, cos θ = OP/CP = x/√(R2 + X2 ) and |dE| = k dq/(R2 + x2)
Therefore, |E| = ∫k × x × dq/(R2 + X2 )(√(R2 + X2 )
|E| = k × q × x/(R2 + X2 )3/2
The direction of E is along the positive x-axis of the loop.
Now, let us talk about the electric field due to a uniformly charged sphere.
Charged sphereElectric Field Outside the Shell
To find out the electric field intensity at a point P outside the spherical shell when OP = r.
The Gaussian surface was taken as a sphere having radius r, while the electric field intensity will remain the same at every point seen on the Gaussian surface.
Thus, Gauss theorem becomes,
∮ \overrightarrow{\rm E}.\overrightarrow{\rm dS} = ∮\overrightarrow{\rm E}.\hat ndS = \frac {q}{\varepsilon_0}
or it can be also be given as,
E∮dS = q/ε0
E × (4πr2) = q/ε0
Therefore, the electric field become,
E = \frac {q}{4 \pi\varepsilon_0}
From the above equation we can say that the electric field outside the shell is similar to the electric field due to a point charge. Thus outside the sphere, the electric field behaves as though it is due to a point charge (carrying all the charge of the shell) at the Centre of the shell.
Electric Field Inside the Shell
If the point P lies inside the spherical shell, then the Gaussian surface is a surface of a sphere having radius r. Since no charge is present inside the spherical shell, the Gaussian surface encloses no charge. Hence, q = 0.
To derive the value you can put the value of q = 0 in the formula E = q/ε0 which will give the result zero.
Electric Field at the Surface of the Shell
At the surface of the shell, r = R
E = q/(4πR2ε0)
If σ is the surface charge density then
q = (4πR2ε0).σ
Since, we have E = q/(4πR2ε0)
Putting value of q = (4πR2ε0).σ we get
E = σ/ε0
Applications of Electric Field
The applications of electric field are mentioned below:
- Electroporation: A technique in which electric fields are used to make pores in cell membranes to insert drugs, medicines, or genes. It is generally used in cloning processes.
- Electric fields play a role in studying tissue dynamics and controlling crystallization processes like nucleation and crystal growth, etc.
- Electric fields are used to impart kinetic energy to charged particles as they travel through the particle accelerator
- Electric fields are used to accelerate charged particles (ions) through a vacuum chamber, allowing scientists to separate ions based on their mass-to-charge ratios
- Electric fields cause polarization of dielectric materials, resulting in the accumulation of electric charge and increased capacitance.
Solved Examples on Electric Field
Example 1. A force of 100 N is acting on the charge 10 μ C at any point. Determine the electric field intensity at that point.
Solution:
Given:
Force F = 100 N
Charge q = 10 μ C
Electric field formula is given by
E = F / q
E = 100N / 10×10−6C
E = 107 N/C.
2. Calculate the electric field at points P, Q for the following two cases.(figure is provided below).
(a) For a charge of +1 µC placed at the origin.
Figure of part a The magnitude of the electric field at point P is
Ep = {1/4πε }(q/r2 )
Ep = (9 × 109 × 1 × 10-6 )/4 = 2.25 × 103 NC-1
Since, the source charges is positive, the electric field points away from the charge,
So the electric field at the point P is given by
\overrightarrow{\rm E} = 2.25 × 103 NC-1
For the point Q;
EQ = 9 × 109 × 1 × 10-6/16 = 0.56 × 103 NC-1
(b)For a charge of -2 µC placed at the origin
Figure for part -bThe magnitude of the electric field at point P is
Ep = {1/4πε }(q/r2 )
Ep = (9 × 109 × 2 × 10-6)/4
Ep = 4.5 × 103 NC-1
Since, the charge is negative, the electric field points towards,
So, the electric field at point P is given by
\overrightarrow{\rm E} = -4.5 × 103 NC-1
For the point Q = (9 × 109 × 1 × 10-6 )/36 = 0.5 × 103 NC-1
Similar Reads
CBSE Class 12 Physics Notes 2023-24 CBSE Class 12 Physics Notes are an essential part of the study material for any student wanting to pursue a career in engineering or a related field. Physics is the subject that helps us understand our surroundings using simple and complex concepts combined. Class 12 physics introduces us to a lot o
10 min read
Chapter 1 - ELECTRIC CHARGES AND FIELDS
Electric Charge and Electric FieldElectric Field is the region around a charge in which another charge experiences an attractive or repulsive force. Electric Field is an important concept in the study of electrostatics which is the branch of physics. Electric Field despite its invisible nature, powers our homes with electricity, tra
15+ min read
Electric ChargeElectric Charge is the basic property of a matter that causes the matter to experience a force when placed in a electromagnetic field. It is the amount of electric energy that is used for various purposes. Electric charges are categorized into two types, that are, Positive ChargeNegative ChargePosit
8 min read
Conductors and InsulatorsWhen humans remove synthetic clothing or sweater, especially in dry weather, he or she often sees a spark or hear a crackling sound. With females' clothing like a polyester saree, this is essentially observed. Another example is Lightning a common form of electric discharge that seen in the sky duri
9 min read
Basic Properties of Electric ChargeElectric Charges are fundamental in the universe. The presence of electric charges are not only seen in the field of science but also in the daily lives of human beings. For instance, rubbing dry hair with a ruler ends up making some hair strands stand up and this happens because electric charges ar
4 min read
Coulomb's LawCoulomb’s Law is defined as a mathematical concept that defines the electric force between charged objects. Columb's Law states that the force between any two charged particles is directly proportional to the product of the charge but is inversely proportional to the square of the distance between t
9 min read
Forces Between Multiple ChargesWhen our synthetic clothing or sweater is removed from our bodies, especially in dry weather, a spark or crackling sound appears. With females' clothing like a polyester saree, this is almost unavoidable. Lightning, in the sky during thunderstorms, is another case of electric discharge. It is an ele
10 min read
Electric FieldElectric field is a fundamental concept in physics, defining the influence that electric charges exert on their surroundings. This field has both direction and magnitude. It guides the movement of charged entities, impacting everything from the spark of static electricity to the functionality of ele
14 min read
Electric Field LinesElectric field lines are a representation used to visualize the electric field surrounding charged objects. They provide a way to understand the direction and strength of the electric field at different points in space. It helps analyze electric fields in various situations, such as around point cha
5 min read
What is Electric Flux?Electric flux is a fundamental concept in physics that helps us understand and quantify the electric field passing through a given surface. It provides a means to describe the flow of electric field lines through an area. Electric flux forms the basis of Gauss's Law, to calculate the net charge encl
12 min read
Electric DipoleAn electric dipole is defined as a pair of equal and opposite electric charges that are separated, by a small distance. An example of an electric dipole includes two atoms separated by small distances. The magnitude of the electric dipole is obtained by taking the product of either of the charge and
11 min read
Continuous Charge DistributionElectric charge is a fundamental feature of matter that regulates how elementary particles are impacted by an electric or magnetic field. Positive and negative electric charge exists in discrete natural units and cannot be manufactured or destroyed. There are two sorts of electric charges: positive
7 min read
Applications of Gauss's LawGauss's Law states that the total electric flux out of a closed surface equals the charge contained inside the surface divided by the absolute permittivity. The electric flux in an area is defined as the electric field multiplied by the surface area projected in a plane perpendicular to the field. N
9 min read
Chapter 2 - ELECTROSTATIC POTENTIAL AND CAPACITANCE
Electric Potential EnergyElectrical potential energy is the cumulative effect of the position and configuration of a charged object and its neighboring charges. The electric potential energy of a charged object governs its motion in the local electric field.Sometimes electrical potential energy is confused with electric pot
15+ min read
Electric Potential Due to a Point ChargeElectric forces are responsible for almost every chemical reaction within the human body. These chemical reactions occur when the atoms and their charges collide together. In this process, some molecules are formed and some change their shape. Electric forces are experienced by charged bodies when t
7 min read
Electric Potential Of A Dipole and System Of ChargesElectric Potential is defined as the force experienced by a charge inside the electric field of any other charge. mathematically it is defined as the ratio of electric potential energy that is required to take a test charge from infinity to a point inside the electric field of any other charge with
7 min read
Equipotential SurfacesWhen an external force acts to do work, moving a body from a point to another against a force like spring force or gravitational force, that work gets collected or stores as the potential energy of the body. When the external force is excluded, the body moves, gaining the kinetic energy and losing a
9 min read
Potential Energy of a System of ChargesWhen an external force works to accomplish work, such as moving a body from one location to another against a force such as spring force or gravitational force, that work is collected and stored as the body's potential energy. When the external force is removed, the body moves, acquiring kinetic ene
11 min read
Potential Energy in an External FieldWhen an external force operates to conduct work, such as moving a body from one location to another against a force like spring force or gravitational force, the work is gathered and stored as potential energy in the body. When an external force is removed, the body moves, acquiring kinetic energy a
11 min read
Electrostatics of ConductorsWhen an external force is used to remove a body from a situation. Point to another in the face of a force like spring or gravitational force That work is stored in the body as potential energy. When the external environment When a force is eliminated, the body moves, gaining and losing kinetic energ
11 min read
Dielectrics and PolarisationHave you noticed how many of the insulators are made of wood, plastic, or glass? But why is that? When we utilise wood or plastic, why don't we receive electric shocks? Why do you only get severe shocks from metal wires? We'll look at dielectrics, polarisation, the dielectric constant, and more in t
10 min read
Capacitor and CapacitanceCapacitor and Capacitance are related to each other as capacitance is nothing but the ability to store the charge of the capacitor. Capacitors are essential components in electronic circuits that store electrical energy in the form of an electric charge. They are widely used in various applications,
11 min read
What is a Parallel Plate Capacitor?Answer: A Parallel Plate Capacitor is a capacitor with two parallel conducting plates separated by an insulating material and capable of storing electrical charge. Capacitance can be defined in Layman's terms as a physical quantity that indicates the ability of a component or circuit to collect and
8 min read
Capacitors in Series and ParallelCapacitors are special devices that can hold electric charges for instantaneous release in an electric circuit. We can easily connect various capacitors together as we connected the resistor together. The capacitor can be connected in series or parallel combinations and can be connected as a mix of
7 min read
Energy stored in a CapacitorCapacitors are used in almost every electronic device around us. From a fan to a chip, there are lots of capacitors of different sizes around us. Theoretically, the basic function of the capacitor is to store energy. Its common usage includes energy storage, voltage spike protection, and signal filt
6 min read
Chapter 3 - CURRENT ELECTRICITY
Electric CurrentElectricity has become an essential part of our everyday life, changing the way we live and work. In the past, people depended on fire for light, warmth, and cooking. Today, we can easily turn on lights, heat our homes, and charge our devices with just a switch or button. This is all possible becaus
10 min read
Electric Current in ConductorsElectric current in conductors is the movement of electric charge through a substance, usually a metallic wire or other conductor. Electric current is the rate at which an electric charge flows past a certain point in a conductor, and it is measured in amperes. When a potential difference (voltage)
8 min read
Ohm's Law - Definition, Formula, Applications, LimitationsAccording to Ohm's law, the voltage or potential difference between two locations is proportional to the current of electricity flowing through the resistance, and the resistance of the circuit is proportional to the current or electricity travelling through the resistance. V=IR is the formula for O
5 min read
Drift VelocityDrift Velocity as the name suggests refers to the slow movement of electrons in the conductor when an Electromotive force(emf) is introduced. Electrons do not move in a straight line in the conductor, but they move randomly in the conductor colliding with the other electrons and atoms exchanging ene
12 min read
Limitations of Ohm's LawOhm’s Law is a relationship between three physical phenomena: current, voltage, and resistance. This relationship was introduced by German physicist George Simon Ohm. That is why the law is well known as Ohm’s law. It states that the amount of steady current through a large number of materials is di
10 min read
ResistivityResistance is the physical property of the material which opposes the current flow in the circuit whereas resistivity is the intrinsic property that helps us understand the relation between the dimension of the substance and the resistance offered by it. In this article, we will learn about Resista
9 min read
Temperature Dependence of ResistanceDevices such as batteries, cells, etc. are essential for maintaining a potential difference across the circuit and are referred to as voltage sources. When a voltage source is connected across a conductor, it creates an electric field which causes the charges to move and this causes current. The val
5 min read
Electrical Energy and PowerElectric energy is the most important form of energy and is widely used in almost all the electrical devices around us. These devices have a rating written on them. That rating is expressed in Watts and intuitively explains the amount of electricity the device will consume. Bigger devices like AC, r
9 min read
Electromotive ForceElectromotive Force or EMF is the work done by the per unit charge while moving from the positive end to the negative end of the battery. It can also be defined as the energy gain per unit charge while moving from the positive end to the negative end of the battery. The battery or the electric gener
10 min read
Combination of Cells in Series and ParallelThere are many resistances in complex electrical circuits. There are methods to calculate the equivalent resistances in case multiple resistances are connected in series or parallel or sometimes in a combination of series and parallel. In many situations, batteries or different types of voltage sour
6 min read
Kirchhoff's LawsKirchhoff's Laws are the basic laws used in electrostatics to solve complex circuit questions. Kirchhoff's Laws were given by Gustav Robert Kirchhoff who was a famous German Physicist. He gave us two laws Kirchhoff’s Current Law and Kirchhoff’s Voltage Law which are discussed in this article.These l
8 min read
Wheatstone BridgeWheatstone bridge is a device that is used to find the resistance of a conductor, in 1842, scientist Wheatstone proposed a theory, which is called the principle of Wheatstone bridge after his name. we can prove or establish the formula for Wheatstone by using Kirchhoff laws. Wheatstone bridge is sim
10 min read
Chapter 4 - MOVING CHARGES AND MAGNETISM
Magnetic Force on a Current carrying WireWhen a charge is moving under the influence of a magnetic field. It experiences forces, which are perpendicular to its movement. This property of charge is exploited in a lot of fields, for example, this phenomenon is used in the making of motors which in turn are useful for producing mechanical for
5 min read
Motion of a Charged Particle in a Magnetic FieldThis has been already learned about the interaction of electric and magnetic fields, as well as the motion of charged particles in the presence of both electric and magnetic fields. We have also deduced the relationship of the force acting on the charged particle, which is given by the Lorentz force
9 min read
Biot-Savart LawThe Biot-Savart equation expresses the magnetic field created by a current-carrying wire. This conductor or wire is represented as a vector quantity called the current element. Lets take a look at the law and formula of biot-savart law in detail, Biot-Savart Law The magnitude of magnetic induction a
7 min read
Magnetic Field on the Axis of a Circular Current LoopMoving charges is an electric current that passes through a fixed point in a fixed period of time. Moving charges are responsible for establishing the magnetic field. The magnetic field is established due to the force exerted by the flow of moving charges. As the magnetic field is established moving
7 min read
Ampere's Circuital Law and Problems on ItAndré-Marie Ampere, a French physicist, proposed Ampere's Circuital Law. Ampere was born in Lyon, France, on January 20, 1775. His father educated him at home, and he showed an affinity for mathematics at a young age. Ampere was a mathematician and physicist best known for his work on electrodynamic
5 min read
Force between Two Parallel Current Carrying ConductorsMoving charges produce an electric field and the rate of flow of charge is known as current. This is the basic concept in Electrostatics. The magnetic effect of electric current is the other important phenomenon related to moving electric charges. Magnetism is generated due to the flow of current. M
8 min read
Current Loop as a Magnetic DipoleWhen a charge move it generates an electric field and the rate of flow of charge is the current in the electric field. This is the basic concept in Electrostatics. The magnetic effect of electric current is the other important concept related to moving electric charges. Magnetism is generated due to
11 min read
Moving Coil GalvanometerHans Christian Oersted discovered in 1820 that a current-carrying conducting wire produces a magnetic field around it. His findings from his experiments are as follows: The magnetic compass needle is aligned tangent to an imaginary circle centered on the current-carrying cable.When the current is re
10 min read
Chapter 5 - MAGNETISM AND MATTER
CHAPTER 6 - ELECTROMAGNETIC INDUCTION
Experiments of Faraday and HenryFor a long time, electricity and magnetism were thought to be separate and unrelated phenomena. Experiments on electric current by Oersted, Ampere and a few others in the early decades of the nineteenth century established the fact that electricity and magnetism are inter-related. They discovered th
5 min read
Magnetic FluxMagnetic Flux is defined as the surface integral of the normal component of the Magnetic Field(B) propagating through that surface. It is indicated by φ or φB. Its SI unit is Weber(Wb). The study of Magnetic Flux is done in Electromagnetism which is a branch of physics that deals with the relation b
6 min read
Faraday’s Laws of Electromagnetic InductionFaraday's Law of Electromagnetic Induction is the basic law of electromagnetism that is used to explain the working of various equipment that includes an electric motor, electric generator, etc. Faraday's law was given by an English scientist Michael Faraday in 1831. According to Faraday's Law of El
10 min read
Lenz's LawLenz law was given by the German scientist Emil Lenz in 1834 this law is based on the principle of conservation of energy and is in accordance with Newton's third law. Lenz law is used to give the direction of induced current in the circuit. In this article, let's learn about Lenz law its formula, e
7 min read
Motional Electromotive ForceThe process of induction occurs when a change in magnetic flux causes an emf to oppose that change. One of the main reasons for the induction process in motion. We can say, for example, that a magnet moving toward a coil generates an emf, and that a coil moving toward a magnet creates a comparable e
14 min read
Inductance - Definition, Derivation, Types, ExamplesMagnetism has a mystical quality about it. Its capacity to change metals like iron, cobalt, and nickel when touched piques children's interest. Repulsion and attraction between the magnetic poles by observing the shape of the magnetic field created by the iron filling surrounding the bar magnet will
13 min read
AC Generator - Principle, Construction, Working, ApplicationsA changing magnetic flux produces a voltage or current in a conductor, which is known as electromagnetic induction. It can happen when a solenoid's magnetic flux is changed by moving a magnet. There will be no generated voltage (electrostatic potential difference) across an electrical wire if the ma
7 min read
CHAPTER 7 - ALTERNATING CURRENT
AC Voltage Applied to a ResistorAlternating Currents are used almost as a standard by electricity distribution companies. In India, 50 Hz Alternating Current is used for domestic and industrial power supply. Many of our devices are in fact nothing but resistances. These resistances cause some voltage drop but since the voltage thi
5 min read
Phasors | Definition, Examples & DiagramPhasor analysis is used to determine the steady-state response to a linear circuit functioning on sinusoidal sources with frequency (f). It is very common. For example, one can use phasor analysis to differentiate the frequency response of a circuit by performing phasor analysis over a range of freq
10 min read
AC Voltage Applied to an InductorAlternating Currents and Voltages vary and change their directions with time. They are widely used in modern-day devices and electrical systems because of their numerous advantages. Circuits in everyday life consist of resistances, capacitors, and inductances. Inductors are devices that store energy
5 min read
AC Voltage Applied to a CapacitorAlternating Currents and Voltages vary and change their directions with time. They are widely used in modern-day devices and electrical systems because of their numerous advantages. Circuits in everyday life consist of resistances, capacitors, and inductance. Capacitors are the devices that accumula
6 min read
Series LCR CircuitsIn contrast to direct current (DC), which travels solely in one direction, Alternating Current (AC) is an electric current that occasionally reverses direction and alters its magnitude constantly over time. Alternating current is the type of electricity that is delivered to companies and homes, and
8 min read
Power Factor in AC circuitThe power factor is determined by the cosine of the phase angle between voltage and current. In AC circuits, the phase angle between voltage and current is aligned, or in other words, zero. But, practically there exists some phase difference between voltage and current. The value of the power factor
8 min read
TransformerA transformer is the simplest device that is used to transfer electrical energy from one alternating-current circuit to another circuit or multiple circuits, through the process of electromagnetic induction. A transformer works on the principle of electromagnetic induction to step up or step down th
15+ min read
CHAPTER 8 - ELECTROMAGNETIC WAVES
CHAPTER 9 - RAY OPTICS AND OPTICAL INSTRUMENTS