Given the number n (n >=0), find its factorial. Factorial of n is defined as 1 x 2 x ... x n. For n = 0, factorial is 1. We are going to discuss iterative and recursive programs in this post.
Examples:
Input: n = 5
Output: 120
Explanation: 5! = 5 * 4 * 3 * 2 * 1 = 120
Input: n = 4
Output: 24
Explanation: 4! = 4 * 3 * 2 * 1 = 24
Input: n = 0
Output: 1
Input: n = 1
Output: 1
Iterative Solution
The idea is simple, we initialize result as 1. Then run a loop from 1 to n and multiply every number with n.
Illustration for n = 4
Initialize res = 1
Run a loop for i = 2 to 4
i = 2 : res = res * 2 = 2
i = 3 : res = res * 3 = 6
i = 4 : res = res * 4 = 24
C++ // C++ program for factorial of a number #include <iostream> using namespace std; // function to find factorial of given number int factorial(int n) { int res = 1; for (int i = 2; i <= n; i++) res *= i; return res; } // Driver code int main() { int num = 5; cout << "Factorial of " << num << " is " << factorial(num) << endl; return 0; } #include <stdio.h> // function to find factorial of given number int factorial(int n) { int res = 1, i; for (i = 2; i <= n; i++) res *= i; return res; } int main() { int num = 5; printf("Factorial of %d is %d", num, factorial(num)); return 0; } // Java program to find factorial of given number class GfG { // Method to find factorial of the given number static int factorial(int n) { int res = 1; for (int i = 2; i <= n; i++) res *= i; return res; } // Driver method public static void main(String[] args) { int num = 5; System.out.println("Factorial of " + num + " is " + factorial(5)); } } # Python 3 program to find # factorial of given number def factorial(n): res = 1 for i in range(2, n + 1): res *= i return res # Driver Code num = 5 print("Factorial of", num, "is", factorial(num)) // C# program to find // factorial of given number using System; class Test { // Method to find factorial // of given number static int factorial(int n) { int res = 1; for (int i = 2; i <= n; i++) res *= i; return res; } // Driver method public static void Main() { int num = 5; Console.WriteLine("Factorial of " + num + " is " + factorial(5)); } } // JavaScript program to find factorial of given number // Method to find factorial of the given number function factorial(n) { let res = 1; for (let i = 2; i <= n; i++) res *= i; return res; } // Driver method let num = 5; console.log("Factorial of " + num + " is " + factorial(5)); <?php // function to find factorial of given number function factorial($n) { $res = 1; for ($i = 2; $i <= $n; $i++) { $res *= $i; } return $res; } // Driver code $num = 5; echo "Factorial of $num is " . factorial($num) . "\n"; ?> OutputFactorial of 5 is 120
Time Complexity: O(n), since we are running a loop from 1 to n.
Auxiliary Space: O(1)
Recursive Solution
Let us first see how we can break factorial(n) into smaller problem and then define recurrance.
- n! = n * (n - 1) * (n - 2) .... 2 * 1
- (n - 1)! = (n - 1) * (n - 2) ... 2 * 1
From the above two equations, we can say that n! = n * (n - 1)!
Since the problem can be broken down into The idea is to define a recursive function, say factorial(n) to calculate the factorial of number n. According to the value of n, we can have two cases:
if n = 0 or n = 1 :
factorial(n) = 1
Else :
factorial(n) = n * factorial(n - 1).
Illustration:
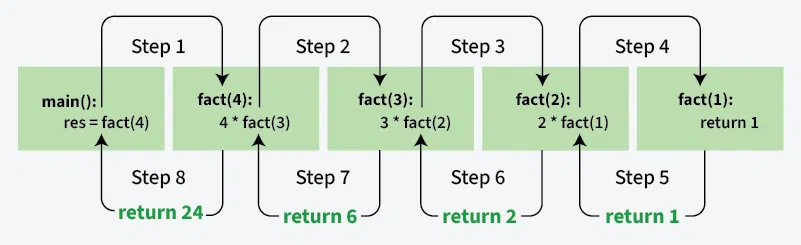
Below is the implementation of the above approach:
C++ // C++ program to find factorial of given number #include <iostream> using namespace std; // Function to find factorial // of given number int factorial(int n) { if (n == 0 || n == 1) return 1; return n * factorial(n - 1); } // Driver code int main() { int num = 5; cout << "Factorial of " << num << " is " << factorial(num) << endl; return 0; } // C program to find factorial of given number #include <stdio.h> // function to find factorial of given number int factorial(int n) { if (n == 0) return 1; return n * factorial(n - 1); } int main() { int num = 5; printf("Factorial of %d is %d", num, factorial(num)); return 0; } // Java program to find factorial of given number class Test { // Method to find factorial of the given number static int factorial(int n) { int res = 1, i; for (i = 2; i <= n; i++) res *= i; return res; } // Driver method public static void main(String[] args) { int num = 5; System.out.println("Factorial of " + num + " is " + factorial(5)); } } # Python 3 program to find # factorial of given number def factorial(n): if n == 0: return 1 return n * factorial(n - 1) # Driver Code num = 5 print(f"Factorial of {num} is {factorial(num)}") // C# program to find factorial // of given number using System; class Test { // method to find factorial // of given number static int factorial(int n) { if (n == 0) return 1; return n * factorial(n - 1); } // Driver method public static void Main() { int num = 5; Console.WriteLine("Factorial of " + num + " is " + factorial(5)); } } // Javascript to find factorial // of given number // function to find factorial // of given number function factorial(n) { if (n == 0) return 1; return n * factorial(n - 1); } // Driver Code let num = 5; console.log("Factorial of " + num + " is " + factorial(num)); <?php // PHP program to find factorial // of given number // function to find factorial // of given number function factorial($n) { if ($n == 0) return 1; return $n * factorial($n - 1); } // Driver Code $num = 5; echo "Factorial of ", $num, " is ", factorial($num); ?> OutputFactorial of 5 is 120
Time Complexity: O(n), since the function is being called n times
Auxiliary Space: O(n), In the worst case, the recursion stack space would be full with all the function calls waiting to get completed and that would make it an O(n) recursion stack space.
Which approach is better - iterative or recursive?
Iterative approach is better as the recursive approach requires extra space for recursion call stack and overhead of recursion calls. However writing a recursive code is always a fun exercise.
How do we handle large numbers?
One simple improvement that we can do is use long long in C/C++ and long in Java/C#, but that does not help much as factorials are really large numbers and causes overflow for small values. Please refer factorial of large number for a solution that works for large numbers.
How to count number of zeroes in factorial?
A simple hint is to count number of times 5 occurs in the factorial. Please refer Count trailing zeroes in factorial of a number for details.
What are the real world applications of factorial?
Factorials are used in permutations and combinations, probability, exponential and logarithmic
Similar Reads
Factorial of a Number Given the number n (n >=0), find its factorial. Factorial of n is defined as 1 x 2 x ... x n. For n = 0, factorial is 1. We are going to discuss iterative and recursive programs in this post.Examples:Input: n = 5Output: 120Explanation: 5! = 5 * 4 * 3 * 2 * 1 = 120Input: n = 4Output: 24Explanation
7 min read
Legendre's formula - Largest power of a prime p in n! Given an integer n and a prime number p, the task is to find the largest x such that px (p raised to power x) divides n!.Examples: Input: n = 7, p = 3Output: x = 2Explanation: 32 divides 7! and 2 is the largest such power of 3.Input: n = 10, p = 3Output: x = 4Explanation: 34 divides 10! and 4 is the
6 min read
Count trailing zeroes in factorial of a number Given an integer n, write a function that returns count of trailing zeroes in n!. Examples : Input: n = 5Output: 1 Explanation: Factorial of 5 is 120 which has one trailing 0.Input: n = 20Output: 4Explanation: Factorial of 20 is 2432902008176640000 which has 4 trailing zeroes.Input: n = 100Output: 2
8 min read
Find the Factorial of a large number Factorial of a non-negative integer, is the multiplication of all integers smaller than or equal to n. Factorial of a numberExamples: Input: 100Output: 933262154439441526816992388562667004- 907159682643816214685929638952175999- 932299156089414639761565182862536979- 2082722375825118521091686400000000
15+ min read
Primorial of a number Given a number n, the task is to calculate its primorial. Primorial (denoted as Pn#) is a product of first n prime numbers. Primorial of a number is similar to the factorial of a number. In primorial, not all the natural numbers get multiplied only prime numbers are multiplied to calculate the primo
10 min read
Find maximum power of a number that divides a factorial Given two numbers, fact and n, find the largest power of n that divides fact! (Factorial of fact). Examples: Input : fact = 5, n = 2 Output : 3 Explanation: Value of 5! is 120. The largest power of 2 that divides 120 is 8 (or 23 Input : fact = 146, n = 15 Output : 35 The idea is based on Legendre’s
12 min read
Largest power of k in n! (factorial) where k may not be prime Given two positive integers k and n, where k > 1, find the largest power of k that divides n! (n factorial).Examples: Input: n = 7, k = 2Output: 4Explanation: 7! = 5040, and 24 = 16 is the highest power of 2 that divides 5040.Input: n = 10, k = 9Output: 2Explanation: 10! = 3628800, and 9² = 81 is
15+ min read
Check if a number is a Krishnamurthy Number or not A Krishnamurthy number is a number whose sum of the factorial of digits is equal to the number itself.For example, 145 is the sum of the factorial of each digit.1! + 4! + 5! = 1 + 24 + 120 = 145 Examples: Input : 145Output : YESExplanation: 1! + 4! + 5! = 1 + 24 + 120 = 145, which is equal to input,
10 min read
Last non-zero digit of a factorial Given a number n, find the last non-zero digit in n!.Examples: Input : n = 5 Output : 2 5! = 5 * 4 * 3 * 2 * 1 = 120 Last non-zero digit in 120 is 2. Input : n = 33 Output : 8 Recommended PracticeLast non-zero digit in factorialTry It! A Simple Solution is to first find n!, then find the last non-ze
14 min read
Count digits in a factorial using Logarithm Given an integer N, find the number of digits that appear in its factorial, where factorial is defined as, factorial(n) = 1*2*3*4........*n and factorial(0) = 1Examples : Input: 5Output: 3Explanation: 5! = 120, i.e., 3 digitsInput: 10Output: 7Explanation: 10! = 3628800, i.e., 7 digits Naive approach
8 min read