You are given a 2D matrix cost[][] of dimensions m × n, where each cell represents the cost of traversing through that position. Your goal is to determine the minimum cost required to reach the bottom-right cell (m-1, n-1) starting from the top-left cell (0,0).
The total cost of a path is the sum of all cell values along the path, including both the starting and ending positions. From any cell (i, j), you can move in the following three directions:
- Right
(i, j+1) - Down
(i+1, j) - Diagonal
(i+1, j+1)
Find the minimum cost path from (0,0) to (m-1, n-1), ensuring that movement constraints are followed.
Example:
Input:

Output: 8
Explanation: The path with minimum cost is highlighted in the following figure. The path is (0, 0) --> (0, 1) --> (1, 2) --> (2, 2). The cost of the path is 8 (1 + 2 + 2 + 3).

[Naive Approach] - Using Recursion - O(3 ^ (m * n)) Time and O(1) Space
The idea is to recursively generate all possible paths from top-left cell to bottom-right cell, and find the path with minimum cost. For the recursive approach, there are three potential cases for each cell in the grid (for any cell at position (m, n)):
- The cost to reach the current cell can be calculated by moving left, i.e., from cell (m, n-1).
- The cost to reach the current cell can also be calculated by moving up, i.e., from cell (m-1, n).
- The cost can also be calculated by moving diagonally, i.e., from cell (m-1, n-1).
Mathematically, the recurrence relation will look like:
minCost(cost, m, n) = cost[m][n] + min(minCost(cost, m, n-1), minCost(cost, m-1, n), minCost(cost, m-1, n-1))
Base Cases:
- if m < 0 or n < 0 (out of bounds) minCost(cost, m, n) = INT_MAX
- minCost(cost, 0, 0) = cost[0][0] as the starting point.
Below is given the implementation:
C++ #include <bits/stdc++.h> using namespace std; // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix int findMinCost(vector<vector<int>>& cost, int x, int y) { int m = cost.size(); int n = cost[0].size(); // If indices are out of bounds, return a large value if (x >= m || y >= m) { return INT_MAX; } // Base case: bottom cell if (x == m - 1 && y == n - 1) { return cost[x][y]; } // Recursively calculate minimum cost from // all possible paths return cost[x][y] + min({findMinCost(cost, x, y + 1), findMinCost(cost, x + 1, y), findMinCost(cost, x + 1, y + 1)}); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) int minCost(vector<vector<int>>& cost) { return findMinCost(cost, 0, 0); } int main() { vector<vector<int>> cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; cout << minCost(cost); return 0; } import java.util.*; class GfG { // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix static int findMinCost(int[][] cost, int x, int y) { int m = cost.length; int n = cost[0].length; // If indices are out of bounds, return a large value if (x >= m || y >= n) { return Integer.MAX_VALUE; } // Base case: bottom cell if (x == m - 1 && y == n - 1) { return cost[x][y]; } // Recursively calculate minimum cost from // all possible paths return cost[x][y] + Math.min( Math.min(findMinCost(cost, x, y + 1), findMinCost(cost, x + 1, y)), findMinCost(cost, x + 1, y + 1)); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) static int minCost(int[][] cost) { return findMinCost(cost, 0, 0); } public static void main(String[] args) { int[][] cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; System.out.println(minCost(cost)); } } import sys # Function to return the cost of the minimum cost path # from (0,0) to (m - 1, n - 1) in a cost matrix def findMinCost(cost, x, y): m = len(cost) n = len(cost[0]) # If indices are out of bounds, return a large value if x >= m or y >= n: return sys.maxsize # Base case: bottom cell if x == m - 1 and y == n - 1: return cost[x][y] # Recursively calculate minimum cost from # all possible paths return cost[x][y] + min(findMinCost(cost, x, y + 1), findMinCost(cost, x + 1, y), findMinCost(cost, x + 1, y + 1)) # function to find the minimum cost path # to reach (m - 1, n - 1) from (0, 0) def minCost(cost): return findMinCost(cost, 0, 0) cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ] print(minCost(cost))
using System; class GfG { // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix static int findMinCost(int[,] cost, int x, int y) { int m = cost.GetLength(0); int n = cost.GetLength(1); // If indices are out of bounds, return a large value if (x >= m || y >= n) { return int.MaxValue; } // Base case: bottom cell if (x == m - 1 && y == n - 1) { return cost[x, y]; } // Recursively calculate minimum cost from // all possible paths return cost[x, y] + Math.Min( Math.Min(findMinCost(cost, x, y + 1), findMinCost(cost, x + 1, y)), findMinCost(cost, x + 1, y + 1)); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) static int minCost(int[,] cost) { return findMinCost(cost, 0, 0); } public static void Main() { int[,] cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; Console.WriteLine(minCost(cost)); } } // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix function findMinCost(cost, x, y) { let m = cost.length; let n = cost[0].length; // If indices are out of bounds, return a large value if (x >= m || y >= n) { return Number.MAX_SAFE_INTEGER; } // Base case: bottom cell if (x === m - 1 && y === n - 1) { return cost[x][y]; } // Recursively calculate minimum cost from // all possible paths return cost[x][y] + Math.min( findMinCost(cost, x, y + 1), findMinCost(cost, x + 1, y), findMinCost(cost, x + 1, y + 1)); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) function minCost(cost) { return findMinCost(cost, 0, 0); } let cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ]; console.log(minCost(cost)); [Expected Approach - 1] - Using Top-Down DP (Memoization) - O(m*n) Time and O(m*n) Space
1. Optimal Substructure:The minimum cost to reach any cell in the grid can be derived from smaller subproblems (i.e., the cost to reach neighboring cells). Specifically, the recursive relation will look like:
minCost(cost, m, n) = cost[m][n] + min(minCost(cost, m, n-1), minCost(cost, m-1, n), minCost(cost, m-1, n-1))
If the last element (i.e., cell (m - 1, n - 1)) is reached, the cost to reach it will be the value of the cell plus the minimum cost to reach one of its valid neighboring cells (left, up, or diagonal).
2. Overlapping Subproblems:
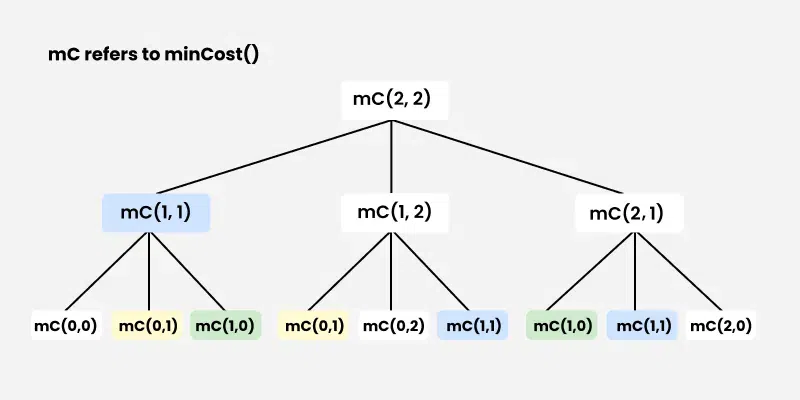
In the recursive approach, subproblems are computed multiple times. For example, when computing the minimum cost from (m, n), we may need to compute the cost for (m-1, n) multiple times. This repetition can be avoided by storing the results of subproblems in a memoization table.
memo[m][n] = cost[m][n] + min(minCost(cost, m, n-1), minCost(cost, m-1, n), minCost(cost, m-1, n-1))
Steps to implement Memoization:
- Create a 2D memo table of size (m x n) to store the computed values, initialized to -1 to indicate uncomputed subproblems.
- If we are at the last cell (m - 1, n - 1), return the value of cost[m - 1][n - 1].
- Before computing the result for any cell (m, n), check if the value at memo[m][n] is already computed. If it is, return the stored value.
- If the value is not computed, recursively calculate the minimum cost and store it in memo[m][n].
- Finally, return the value in memo[0][0] for the minimum cost to reach the target cell (m-1, n-1).
Below is given the implementation:
C++ #include <bits/stdc++.h> using namespace std; // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix int findMinCost(vector<vector<int>>& cost, int x, int y, vector<vector<int>> &memo) { int m = cost.size(); int n = cost[0].size(); // If indices are out of bounds, return a large value if (x >= m || y >= m) { return INT_MAX; } // Base case: bottom cell if (x == m - 1 && y == n - 1) { return cost[x][y]; } // Check if the result is already computed if (memo[x][y] != -1) { return memo[x][y]; } // Recursively calculate minimum cost from // all possible paths return memo[x][y] = cost[x][y] + min({findMinCost(cost, x, y + 1, memo), findMinCost(cost, x + 1, y, memo), findMinCost(cost, x + 1, y + 1, memo)}); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) int minCost(vector<vector<int>>& cost) { int m = cost.size(); int n = cost[0].size(); // create 2d array to store the minimum cost path vector<vector<int>> memo(m, vector<int>(n, -1)); return findMinCost(cost, 0, 0, memo); } int main() { vector<vector<int>> cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; cout << minCost(cost); return 0; } import java.util.*; class GfG { // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix static int findMinCost(int[][] cost, int x, int y, int[][] memo) { int m = cost.length; int n = cost[0].length; // If indices are out of bounds, return a large value if (x >= m || y >= n) { return Integer.MAX_VALUE; } // Base case: bottom cell if (x == m - 1 && y == n - 1) { return cost[x][y]; } // Check if the result is already computed if (memo[x][y] != -1) { return memo[x][y]; } // Recursively calculate minimum cost from // all possible paths return memo[x][y] = cost[x][y] + Math.min(Math.min(findMinCost(cost, x, y + 1, memo), findMinCost(cost, x + 1, y, memo)), findMinCost(cost, x + 1, y + 1, memo)); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) static int minCost(int[][] cost) { int m = cost.length; int n = cost[0].length; // create 2d array to store the minimum cost path int[][] memo = new int[m][n]; for (int[] row : memo) { Arrays.fill(row, -1); } return findMinCost(cost, 0, 0, memo); } public static void main(String[] args) { int[][] cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; System.out.println(minCost(cost)); } } import sys # Function to return the cost of the minimum cost path # from (0,0) to (m - 1, n - 1) in a cost matrix def findMinCost(cost, x, y, memo): m = len(cost) n = len(cost[0]) # If indices are out of bounds, return a large value if x >= m or y >= n: return sys.maxsize # Base case: bottom cell if x == m - 1 and y == n - 1: return cost[x][y] # Check if the result is already computed if memo[x][y] != -1: return memo[x][y] # Recursively calculate minimum cost from # all possible paths memo[x][y] = cost[x][y] + min( findMinCost(cost, x, y + 1, memo), findMinCost(cost, x + 1, y, memo), findMinCost(cost, x + 1, y + 1, memo)) return memo[x][y] # function to find the minimum cost path # to reach (m - 1, n - 1) from (0, 0) def minCost(cost): m = len(cost) n = len(cost[0]) # create 2d array to store the minimum cost path memo = [[-1] * n for _ in range(m)] return findMinCost(cost, 0, 0, memo) cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ] print(minCost(cost))
using System; class GfG { // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix static int findMinCost(int[,] cost, int x, int y, int[,] memo) { int m = cost.GetLength(0); int n = cost.GetLength(1); // If indices are out of bounds, return a large value if (x >= m || y >= n) { return int.MaxValue; } // Base case: bottom cell if (x == m - 1 && y == n - 1) { return cost[x, y]; } // Check if the result is already computed if (memo[x, y] != -1) { return memo[x, y]; } // Recursively calculate minimum cost from // all possible paths return memo[x, y] = cost[x, y] + Math.Min(Math.Min(findMinCost(cost, x, y + 1, memo), findMinCost(cost, x + 1, y, memo)), findMinCost(cost, x + 1, y + 1, memo)); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) static int minCost(int[,] cost) { int m = cost.GetLength(0); int n = cost.GetLength(1); // create 2d array to store the minimum cost path int[,] memo = new int[m, n]; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { memo[i, j] = -1; } } return findMinCost(cost, 0, 0, memo); } public static void Main() { int[,] cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; Console.WriteLine(minCost(cost)); } } // Function to return the cost of the minimum cost path // from (0,0) to (m - 1, n - 1) in a cost matrix function findMinCost(cost, x, y, memo) { let m = cost.length; let n = cost[0].length; // If indices are out of bounds, return a large value if (x >= m || y >= n) { return Number.MAX_SAFE_INTEGER; } // Base case: bottom cell if (x === m - 1 && y === n - 1) { return cost[x][y]; } // Check if the result is already computed if (memo[x][y] !== -1) { return memo[x][y]; } // Recursively calculate minimum cost from // all possible paths return memo[x][y] = cost[x][y] + Math.min( findMinCost(cost, x, y + 1, memo), findMinCost(cost, x + 1, y, memo), findMinCost(cost, x + 1, y + 1, memo)); } // function to find the minimum cost path // to reach (m - 1, n - 1) from (0, 0) function minCost(cost) { let m = cost.length; let n = cost[0].length; // create 2d array to store the minimum cost path let memo = Array.from({ length: m }, () => Array(n).fill(-1)); return findMinCost(cost, 0, 0, memo); } let cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ]; console.log(minCost(cost)); [Expected Approach - 2] - Using Bottom-Up DP (Tabulation) - O(m * n) Time and O(m * n) Space
The approach here is similar to the recursive one but instead of breaking down the problem recursively, we iteratively build up the solution by calculating it in a bottom-up manner. We create a 2D array dp of size m*n where dp[i][j] represents the minimum cost to reach cell (i, j).
Dynamic Programming Relation:
Initialize the base case: dp[0][0] = cost[0][0]
- For the first row (dp[0][j]), we can only move from the left: dp[0][j] = dp[0][j - 1] + cost[0][j] for j > 0
- For the first column (dp[i][0]), we can only move from the top: dp[i][0] = dp[i - 1][0] + cost[i][0] for i > 0
For the rest of the cells, we calculate the minimum cost by considering the minimum cost from three directions: from the left, from above, and from the diagonal:
- dp[i][j] = cost[i][j] + min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1])
This formula ensures that at each step, we are choosing the minimum cost path to reach the current cell.
Below is given the implementation:
C++ // C++ implementation to find the minimum cost path // using Tabulation (Dynamic Programming) #include <bits/stdc++.h> using namespace std; int minCost(vector<vector<int>>& cost) { int m = cost.size(); int n = cost[0].size(); vector<vector<int>> dp(m, vector<int>(n, 0)); // Initialize the base cell dp[0][0] = cost[0][0]; // Fill the first row for (int j = 1; j < n; j++) { dp[0][j] = dp[0][j - 1] + cost[0][j]; } // Fill the first column for (int i = 1; i < m; i++) { dp[i][0] = dp[i - 1][0] + cost[i][0]; } // Fill the rest of the dp table for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { dp[i][j] = cost[i][j] + min({dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]}); } } return dp[m - 1][n - 1]; } int main() { vector<vector<int>> cost = { {1, 2, 3}, {4, 8, 2}, {1, 5, 3} }; cout << minCost(cost); return 0; } // Java implementation to find the minimum cost path // using Tabulation (Dynamic Programming) import java.util.ArrayList; import java.util.List; class GfG { static int minCost(List<List<Integer>> cost) { int m = cost.size(); int n = cost.get(0).size(); int[][] dp = new int[m][n]; // Initialize the base cell dp[0][0] = cost.get(0).get(0); // Fill the first row for (int j = 1; j < n; j++) { dp[0][j] = dp[0][j - 1] + cost.get(0).get(j); } // Fill the first column for (int i = 1; i < m; i++) { dp[i][0] = dp[i - 1][0] + cost.get(i).get(0); } // Fill the rest of the dp table for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { dp[i][j] = cost.get(i).get(j) + Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])); } } // Minimum cost to reach the bottom-right cell return dp[m - 1][n - 1]; } public static void main(String[] args) { List<List<Integer>> cost = new ArrayList<>(); cost.add(List.of(1, 2, 3)); cost.add(List.of(4, 8, 2)); cost.add(List.of(1, 5, 3)); System.out.println(minCost(cost)); } } # Python implementation to find the minimum cost path # using Tabulation (Dynamic Programming) def mincost(cost): m = len(cost) n = len(cost[0]) dp = [[0] * n for _ in range(m)] # Initialize the base cell dp[0][0] = cost[0][0] # Fill the first row for j in range(1, n): dp[0][j] = dp[0][j - 1] + cost[0][j] # Fill the first column for i in range(1, m): dp[i][0] = dp[i - 1][0] + cost[i][0] # Fill the rest of the dp table for i in range(1, m): for j in range(1, n): dp[i][j] = cost[i][j] \ + min(dp[i - 1][j], \ dp[i][j - 1], dp[i - 1][j - 1]) # Minimum cost to reach the # bottom-right cell return dp[m - 1][n - 1] if __name__ == "__main__": cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ] print(mincost(cost))
// C# implementation to find the minimum cost path // using Tabulation (Dynamic Programming) using System; using System.Collections.Generic; class GfG { static int MinCost(List<List<int>> cost) { int m = cost.Count; int n = cost[0].Count; int[,] dp = new int[m, n]; // Initialize the base cell dp[0, 0] = cost[0][0]; // Fill the first row for (int j = 1; j < n; j++) { dp[0, j] = dp[0, j - 1] + cost[0][j]; } // Fill the first column for (int i = 1; i < m; i++) { dp[i, 0] = dp[i - 1, 0] + cost[i][0]; } // Fill the rest of the dp table for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { dp[i, j] = cost[i][j] + Math.Min(dp[i - 1, j], Math.Min(dp[i, j - 1], dp[i - 1, j - 1])); } } // Minimum cost to reach the // bottom-right cell return dp[m - 1, n - 1]; } static void Main() { List<List<int>> cost = new List<List<int>> { new List<int> { 1, 2, 3 }, new List<int> { 4, 8, 2 }, new List<int> { 1, 5, 3 } }; Console.WriteLine(MinCost(cost)); } } // JavaScript implementation to find the minimum cost path // using Tabulation (Dynamic Programming) function minCost(cost) { const m = cost.length; const n = cost[0].length; const dp = Array.from({ length: m }, () => Array(n).fill(0)); // Initialize the base cell dp[0][0] = cost[0][0]; // Fill the first row for (let j = 1; j < n; j++) { dp[0][j] = dp[0][j - 1] + cost[0][j]; } // Fill the first column for (let i = 1; i < m; i++) { dp[i][0] = dp[i - 1][0] + cost[i][0]; } // Fill the rest of the dp table for (let i = 1; i < m; i++) { for (let j = 1; j < n; j++) { dp[i][j] = cost[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]); } } // Minimum cost to reach the bottom-right cell return dp[m - 1][n - 1]; } const cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ]; console.log(minCost(cost)); [Optimal Approach] - Using Space Optimized DP - O(m * n) Time and O(n) Space
In the previous approach, we used a 2D dp table to store the minimum cost at each cell. However, we can optimize the space complexity by observing that for calculating the current state, we only need the values from the previous row. Therefore, there is no need to store the entire dp table, and we can optimize the space to O(n) by only keeping track of the current and previous rows.
Below is given the implementation:
C++ // C++ implementation to find the minimum cost path // using Space Optimization #include <bits/stdc++.h> using namespace std; int minCost(vector<vector<int>> &cost) { int m = cost.size(); int n = cost[0].size(); // 1D dp array to store the minimum cost // of the current row vector<int> dp(n, 0); // Initialize the base cell dp[0] = cost[0][0]; // Fill the first row for (int j = 1; j < n; j++) { dp[j] = dp[j - 1] + cost[0][j]; } // Fill the rest of the rows for (int i = 1; i < m; i++) { // Store the previous value of dp[j-1] // (for diagonal handling) int prev = dp[0]; // Update the first column (only depends on // the previous row) dp[0] = dp[0] + cost[i][0]; for (int j = 1; j < n; j++) { // Store the current dp[j] before updating it int temp = dp[j]; // Update dp[j] using the minimum of the // top, left, and diagonal cells dp[j] = cost[i][j] + min({dp[j], dp[j - 1], prev}); // Update prev to be the old dp[j] for the // diagonal calculation in the next iteration prev = temp; } } // The last cell contains the // minimum cost path return dp[n - 1]; } int main() { vector<vector<int>> cost = {{1, 2, 3}, {4, 8, 2}, {1, 5, 3}}; cout << minCost(cost) << endl; return 0; } // Java implementation to find the minimum cost path // using Space Optimization import java.util.*; class GfG { static int minCost(int[][] cost) { int m = cost.length; int n = cost[0].length; // 1D dp array to store the minimum cost of the // current row int[] dp = new int[n]; // Initialize the base cell dp[0] = cost[0][0]; // Fill the first row for (int j = 1; j < n; j++) { dp[j] = dp[j - 1] + cost[0][j]; } // Fill the rest of the rows for (int i = 1; i < m; i++) { // Store the previous value of dp[j-1] (for // diagonal handling) int prev = dp[0]; // Update the first column (only depends on the // previous row) dp[0] = dp[0] + cost[i][0]; for (int j = 1; j < n; j++) { // Store the current dp[j] before updating // it int temp = dp[j]; // Update dp[j] using the minimum of the // top, left, and diagonal cells dp[j] = cost[i][j] + Math.min(dp[j], Math.min(dp[j - 1], prev)); // Update prev to be the old dp[j] for the // diagonal calculation in the next // iteration prev = temp; } } // The last cell contains the minimum cost path return dp[n - 1]; } public static void main(String[] args) { int[][] cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; System.out.println(minCost(cost)); } } # Python implementation to find the minimum cost path # using Space Optimization def minCost(cost): m = len(cost) n = len(cost[0]) # 1D dp array to store the minimum # cost of the current row dp = [0] * n # Initialize the base cell dp[0] = cost[0][0] # Fill the first row for j in range(1, n): dp[j] = dp[j - 1] + cost[0][j] # Fill the rest of the rows for i in range(1, m): # Store the previous value of dp[j-1] # (for diagonal handling) prev = dp[0] # Update the first column (only depends # on the previous row) dp[0] = dp[0] + cost[i][0] for j in range(1, n): # Store the current dp[j] before # updating it temp = dp[j] # Update dp[j] using the minimum of the top, # left, and diagonal cells dp[j] = cost[i][j] + min(dp[j], dp[j - 1], prev) # Update prev to be the old dp[j] for the # diagonal calculation in the next iteration prev = temp # The last cell contains the minimum # cost path return dp[n - 1] cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ] print(minCost(cost))
// C# implementation to find the minimum cost path // using Space Optimization using System; class GfG { static int MinCost(int[, ] cost) { int m = cost.GetLength(0); int n = cost.GetLength(1); // 1D dp array to store the minimum cost of the // current row int[] dp = new int[n]; // Initialize the base cell dp[0] = cost[0, 0]; // Fill the first row for (int j = 1; j < n; j++) { dp[j] = dp[j - 1] + cost[0, j]; } // Fill the rest of the rows for (int i = 1; i < m; i++) { // Store the previous value of dp[j-1] (for // diagonal handling) int prev = dp[0]; // Update the first column (only depends on the // previous row) dp[0] = dp[0] + cost[i, 0]; for (int j = 1; j < n; j++) { // Store the current dp[j] before updating // it int temp = dp[j]; // Update dp[j] using the minimum of the // top, left, and diagonal cells dp[j] = cost[i, j] + Math.Min(dp[j], Math.Min(dp[j - 1], prev)); // Update prev to be the old dp[j] for the // diagonal calculation in the next // iteration prev = temp; } } // The last cell contains the minimum cost path return dp[n - 1]; } static void Main(string[] args) { int[, ] cost = { { 1, 2, 3 }, { 4, 8, 2 }, { 1, 5, 3 } }; Console.WriteLine(MinCost(cost)); } } // JavaScript implementation to find the minimum cost path // using Space Optimization function minCost(cost) { const m = cost.length; const n = cost[0].length; // 1D dp array to store the minimum cost of the current // row let dp = new Array(n); // Initialize the base cell dp[0] = cost[0][0]; // Fill the first row for (let j = 1; j < n; j++) { dp[j] = dp[j - 1] + cost[0][j]; } // Fill the rest of the rows for (let i = 1; i < m; i++) { // Store the previous value of dp[j-1] (for diagonal // handling) let prev = dp[0]; // Update the first column (only depends on the // previous row) dp[0] = dp[0] + cost[i][0]; for (let j = 1; j < n; j++) { // Store the current dp[j] before updating it let temp = dp[j]; // Update dp[j] using the minimum of the top, // left, and diagonal cells dp[j] = cost[i][j] + Math.min(dp[j], Math.min(dp[j - 1], prev)); // Update prev to be the old dp[j] for the // diagonal calculation in the next iteration prev = temp; } } // The last cell contains the minimum cost path return dp[n - 1]; } const cost = [ [ 1, 2, 3 ], [ 4, 8, 2 ], [ 1, 5, 3 ] ]; console.log(minCost(cost));
[Alternate Less Efficient Approach] - Using Dijkstra's Algorithm - O((m * n) * log(m * n)) Time and O(m * n) Space
The idea is to apply Dijskra's Algorithm to find the minimum cost path from the top-left to the bottom-right corner of the grid. Each cell is treated as a node and each move between adjacent cells has a cost. We use a min-heap to always expand the least costly path first.
C++ // C++ implementation to find minimum cost path // using Dijstra's Algoritms #include <bits/stdc++.h> using namespace std; int minCost(vector<vector<int>> &cost) { int m = cost.size(); int n = cost[0].size(); // Directions for moving down, right, and diagonal vector<pair<int, int>> directions = {{1, 0}, {0, 1}, {1, 1}}; // Min-heap (priority queue) for Dijkstra's algorithm priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq; // Distance matrix to store the minimum // cost to reach each cell vector<vector<int>> dist(m, vector<int>(n, INT_MAX)); dist[0][0] = cost[0][0]; pq.push({cost[0][0], 0, 0}); // Prim's algorithm while (!pq.empty()) { vector<int> curr = pq.top(); pq.pop(); int x = curr[1]; int y = curr[2]; // If we reached the bottom-right // corner, return the cost if (x == m - 1 && y == n - 1) { return dist[x][y]; } // Explore the neighbors for (auto &dir : directions) { int newX = x + dir.first; int newY = y + dir.second; // Ensure the new cell is within bounds if (newX < m && newY < n) { // Relaxation step if (dist[newX][newY] > dist[x][y] + cost[newX][newY]) { dist[newX][newY] = dist[x][y] + cost[newX][newY]; pq.push({dist[newX][newY], newX, newY}); } } } } return dist[m - 1][n - 1]; } int main() { vector<vector<int>> cost = { {1, 2, 3}, {4, 8, 2}, {1, 5, 3} }; cout << minCost(cost); return 0; } import java.util.*; class GfG { int minCost(int[][] cost) { int m = cost.length; int n = cost[0].length; // Directions for moving down, right, and diagonal int[][] directions = {{1, 0}, {0, 1}, {1, 1}}; // Min-heap (priority queue) for Dijkstra's algorithm PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0])); // Distance matrix to store the minimum // cost to reach each cell int[][] dist = new int[m][n]; for (int[] row : dist) { Arrays.fill(row, Integer.MAX_VALUE); } dist[0][0] = cost[0][0]; pq.add(new int[]{cost[0][0], 0, 0}); // Prim's algorithm while (!pq.isEmpty()) { int[] curr = pq.poll(); int x = curr[1]; int y = curr[2]; // If we reached the bottom-right // corner, return the cost if (x == m - 1 && y == n - 1) { return dist[x][y]; } // Explore the neighbors for (int[] dir : directions) { int newX = x + dir[0]; int newY = y + dir[1]; // Ensure the new cell is within bounds if (newX < m && newY < n) { // Relaxation step if (dist[newX][newY] > dist[x][y] + cost[newX][newY]) { dist[newX][newY] = dist[x][y] + cost[newX][newY]; pq.add(new int[]{dist[newX][newY], newX, newY}); } } } } return dist[m - 1][n - 1]; } public static void main(String[] args) { int[][] cost = { {1, 2, 3}, {4, 8, 2}, {1, 5, 3} }; GfG obj = new GfG(); System.out.println(obj.minCost(cost)); } } import heapq def minCost(cost): m = len(cost) n = len(cost[0]) # Directions for moving down, right, and diagonal directions = [(1, 0), (0, 1), (1, 1)] # Min-heap (priority queue) for Dijkstra's algorithm pq = [] # Distance matrix to store the minimum # cost to reach each cell dist = [[float('inf')] * n for _ in range(m)] dist[0][0] = cost[0][0] heapq.heappush(pq, (cost[0][0], 0, 0)) # Prim's algorithm while pq: curr = heapq.heappop(pq) x = curr[1] y = curr[2] # If we reached the bottom-right # corner, return the cost if x == m - 1 and y == n - 1: return dist[x][y] # Explore the neighbors for dx, dy in directions: newX = x + dx newY = y + dy # Ensure the new cell is within bounds if newX < m and newY < n: # Relaxation step if dist[newX][newY] > dist[x][y] + cost[newX][newY]: dist[newX][newY] = dist[x][y] + cost[newX][newY] heapq.heappush(pq, (dist[newX][newY], newX, newY)) return dist[m - 1][n - 1] cost = [ [1, 2, 3], [4, 8, 2], [1, 5, 3] ] print(minCost(cost)) using System; using System.Collections.Generic; class GfG { int minCost(int[,] cost) { int m = cost.GetLength(0); int n = cost.GetLength(1); // Directions for moving down, right, and diagonal int[,] directions = { {1, 0}, {0, 1}, {1, 1} }; // Min-heap (priority queue) for Dijkstra's algorithm SortedSet<(int, int, int)> pq = new SortedSet<(int, int, int)> (Comparer<(int, int, int)>.Create((a, b) => a.Item1 == b.Item1 ? (a.Item2 == b.Item2 ? a.Item3 - b.Item3 : a.Item2 - b.Item2) : a.Item1 - b.Item1)); // Distance matrix to store the minimum // cost to reach each cell int[,] dist = new int[m, n]; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { dist[i, j] = int.MaxValue; } } dist[0, 0] = cost[0, 0]; pq.Add((cost[0, 0], 0, 0)); // Prim's algorithm while (pq.Count > 0) { var curr = pq.Min; pq.Remove(curr); int x = curr.Item2; int y = curr.Item3; // If we reached the bottom-right // corner, return the cost if (x == m - 1 && y == n - 1) { return dist[x, y]; } // Explore the neighbors for (int i = 0; i < 3; i++) { int newX = x + directions[i, 0]; int newY = y + directions[i, 1]; // Ensure the new cell is within bounds if (newX < m && newY < n) { // Relaxation step if (dist[newX, newY] > dist[x, y] + cost[newX, newY]) { dist[newX, newY] = dist[x, y] + cost[newX, newY]; pq.Add((dist[newX, newY], newX, newY)); } } } } return dist[m - 1, n - 1]; } public static void Main() { int[,] cost = { {1, 2, 3}, {4, 8, 2}, {1, 5, 3} }; GfG obj = new GfG(); Console.WriteLine(obj.minCost(cost)); } } function minCost(cost) { let m = cost.length; let n = cost[0].length; // Directions for moving down, right, and diagonal let directions = [[1, 0], [0, 1], [1, 1]]; // Min-heap (priority queue) for Dijkstra's algorithm let pq = []; // Distance matrix to store the minimum // cost to reach each cell let dist = Array.from({ length: m }, () => Array(n).fill(Infinity)); dist[0][0] = cost[0][0]; pq.push([cost[0][0], 0, 0]); // Prim's algorithm while (pq.length > 0) { pq.sort((a, b) => a[0] - b[0]); let [currCost, x, y] = pq.shift(); // If we reached the bottom-right // corner, return the cost if (x === m - 1 && y === n - 1) { return dist[x][y]; } // Explore the neighbors for (let [dx, dy] of directions) { let newX = x + dx; let newY = y + dy; // Ensure the new cell is within bounds if (newX < m && newY < n) { // Relaxation step if (dist[newX][newY] > dist[x][y] + cost[newX][newY]) { dist[newX][newY] = dist[x][y] + cost[newX][newY]; pq.push([dist[newX][newY], newX, newY]); } } } } return dist[m - 1][n - 1]; } console.log(minCost([[1, 2, 3], [4, 8, 2], [1, 5, 3]])); Similar Reads
Dynamic Programming or DP Dynamic Programming is an algorithmic technique with the following properties.It is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for the same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of
3 min read
What is Memoization? A Complete Tutorial In this tutorial, we will dive into memoization, a powerful optimization technique that can drastically improve the performance of certain algorithms. Memoization helps by storing the results of expensive function calls and reusing them when the same inputs occur again. This avoids redundant calcula
6 min read
Dynamic Programming (DP) Introduction Dynamic Programming is a commonly used algorithmic technique used to optimize recursive solutions when same subproblems are called again.The core idea behind DP is to store solutions to subproblems so that each is solved only once. To solve DP problems, we first write a recursive solution in a way t
15+ min read
Tabulation vs Memoization Tabulation and memoization are two techniques used to implement dynamic programming. Both techniques are used when there are overlapping subproblems (the same subproblem is executed multiple times). Below is an overview of two approaches.Memoization:Top-down approachStores the results of function ca
9 min read
Optimal Substructure Property in Dynamic Programming | DP-2 The following are the two main properties of a problem that suggest that the given problem can be solved using Dynamic programming: 1) Overlapping Subproblems 2) Optimal Substructure We have already discussed the Overlapping Subproblem property. Let us discuss the Optimal Substructure property here.
3 min read
Overlapping Subproblems Property in Dynamic Programming | DP-1 Dynamic Programming is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems using recursion and storing the results of subproblems to avoid computing the same results again. Following are the two main properties of a problem that suggests that the given problem
10 min read
Steps to solve a Dynamic Programming Problem Steps to solve a Dynamic programming problem:Identify if it is a Dynamic programming problem.Decide a state expression with the Least parameters.Formulate state and transition relationship.Apply tabulation or memorization.Step 1: How to classify a problem as a Dynamic Programming Problem? Typically,
13 min read
Advanced Topics
Count Ways To Assign Unique Cap To Every PersonGiven n people and 100 types of caps labelled from 1 to 100, along with a 2D integer array caps where caps[i] represents the list of caps preferred by the i-th person, the task is to determine the number of ways the n people can wear different caps.Example:Input: caps = [[3, 4], [4, 5], [5]] Output:
15+ min read
Digit DP | IntroductionPrerequisite : How to solve a Dynamic Programming Problem ?There are many types of problems that ask to count the number of integers 'x' between two integers say 'a' and 'b' such that x satisfies a specific property that can be related to its digits.So, if we say G(x) tells the number of such intege
14 min read
Sum over Subsets | Dynamic ProgrammingPrerequisite: Basic Dynamic Programming, Bitmasks Consider the following problem where we will use Sum over subset Dynamic Programming to solve it. Given an array of 2n integers, we need to calculate function F(x) = ?Ai such that x&i==i for all x. i.e, i is a bitwise subset of x. i will be a bit
10 min read
Easy problems in Dynamic programming
Coin Change - Count Ways to Make SumGiven an integer array of coins[] of size n representing different types of denominations and an integer sum, the task is to count all combinations of coins to make a given value sum. Note: Assume that you have an infinite supply of each type of coin. Examples: Input: sum = 4, coins[] = [1, 2, 3]Out
15+ min read
Subset Sum ProblemGiven an array arr[] of non-negative integers and a value sum, the task is to check if there is a subset of the given array whose sum is equal to the given sum. Examples: Input: arr[] = [3, 34, 4, 12, 5, 2], sum = 9Output: TrueExplanation: There is a subset (4, 5) with sum 9.Input: arr[] = [3, 34, 4
15+ min read
Introduction and Dynamic Programming solution to compute nCr%pGiven three numbers n, r and p, compute value of nCr mod p. Example: Input: n = 10, r = 2, p = 13 Output: 6 Explanation: 10C2 is 45 and 45 % 13 is 6.We strongly recommend that you click here and practice it, before moving on to the solution.METHOD 1: (Using Dynamic Programming) A Simple Solution is
15+ min read
Rod CuttingGiven a rod of length n inches and an array price[]. price[i] denotes the value of a piece of length i. The task is to determine the maximum value obtainable by cutting up the rod and selling the pieces.Note: price[] is 1-indexed array.Input: price[] = [1, 5, 8, 9, 10, 17, 17, 20]Output: 22Explanati
15+ min read
Painting Fence AlgorithmGiven a fence with n posts and k colors, the task is to find out the number of ways of painting the fence so that not more than two consecutive posts have the same color.Examples:Input: n = 2, k = 4Output: 16Explanation: We have 4 colors and 2 posts.Ways when both posts have same color: 4 Ways when
15 min read
Longest Common Subsequence (LCS)Given two strings, s1 and s2, the task is to find the length of the Longest Common Subsequence. If there is no common subsequence, return 0. A subsequence is a string generated from the original string by deleting 0 or more characters, without changing the relative order of the remaining characters.
15+ min read
Longest Increasing Subsequence (LIS)Given an array arr[] of size n, the task is to find the length of the Longest Increasing Subsequence (LIS) i.e., the longest possible subsequence in which the elements of the subsequence are sorted in increasing order.Examples: Input: arr[] = [3, 10, 2, 1, 20]Output: 3Explanation: The longest increa
14 min read
Longest subsequence such that difference between adjacents is oneGiven an array arr[] of size n, the task is to find the longest subsequence such that the absolute difference between adjacent elements is 1.Examples: Input: arr[] = [10, 9, 4, 5, 4, 8, 6]Output: 3Explanation: The three possible subsequences of length 3 are [10, 9, 8], [4, 5, 4], and [4, 5, 6], wher
15+ min read
Maximum size square sub-matrix with all 1sGiven a binary matrix mat of size n * m, the task is to find out the maximum length of a side of a square sub-matrix with all 1s.Example:Input: mat = [ [0, 1, 1, 0, 1], [1, 1, 0, 1, 0], [0, 1, 1, 1, 0], [1, 1, 1, 1, 0], [1, 1, 1, 1, 1], [0, 0, 0, 0, 0] ]Output: 3Explanation: The maximum length of a
15+ min read
Min Cost PathYou are given a 2D matrix cost[][] of dimensions m × n, where each cell represents the cost of traversing through that position. Your goal is to determine the minimum cost required to reach the bottom-right cell (m-1, n-1) starting from the top-left cell (0,0).The total cost of a path is the sum of
15+ min read
Longest Common Substring (Space optimized DP solution)Given two strings ‘s1‘ and ‘s2‘, find the length of the longest common substring. Example: Input: s1 = “GeeksforGeeksâ€, s2 = “GeeksQuiz†Output : 5 Explanation:The longest common substring is “Geeks†and is of length 5.Input: s1 = “abcdxyzâ€, s2 = “xyzabcd†Output : 4Explanation:The longest common su
7 min read
Count ways to reach the nth stair using step 1, 2 or 3A child is running up a staircase with n steps and can hop either 1 step, 2 steps, or 3 steps at a time. The task is to implement a method to count how many possible ways the child can run up the stairs.Examples: Input: 4Output: 7Explanation: There are seven ways: {1, 1, 1, 1}, {1, 2, 1}, {2, 1, 1},
15+ min read
Grid Unique Paths - Count Paths in matrixGiven an matrix of size m x n, the task is to find the count of all unique possible paths from top left to the bottom right with the constraints that from each cell we can either move only to the right or down.Examples: Input: m = 2, n = 2Output: 2Explanation: There are two paths(0, 0) -> (0, 1)
15+ min read
Unique paths in a Grid with ObstaclesGiven a matrix mat[][] of size n * m, where mat[i][j] = 1 indicates an obstacle and mat[i][j] = 0 indicates an empty space. The task is to find the number of unique paths to reach (n-1, m-1) starting from (0, 0). You are allowed to move in the right or downward direction. Note: In the grid, cells ma
15+ min read
Medium problems on Dynamic programming
0/1 Knapsack ProblemGiven n items where each item has some weight and profit associated with it and also given a bag with capacity W, [i.e., the bag can hold at most W weight in it]. The task is to put the items into the bag such that the sum of profits associated with them is the maximum possible. Note: The constraint
15+ min read
Printing Items in 0/1 KnapsackGiven weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays, val[0..n-1] and wt[0..n-1] represent values and weights associated with n items respectively. Also given an integer W which repre
12 min read
Unbounded Knapsack (Repetition of items allowed)Given a knapsack weight, say capacity and a set of n items with certain value vali and weight wti, The task is to fill the knapsack in such a way that we can get the maximum profit. This is different from the classical Knapsack problem, here we are allowed to use an unlimited number of instances of
15+ min read
Egg Dropping Puzzle | DP-11You are given n identical eggs and you have access to a k-floored building from 1 to k.There exists a floor f where 0 <= f <= k such that any egg dropped from a floor higher than f will break, and any egg dropped from or below floor f will not break. There are a few rules given below:An egg th
15+ min read
Word BreakGiven a string s and y a dictionary of n words dictionary, check if s can be segmented into a sequence of valid words from the dictionary, separated by spaces.Examples:Input: s = "ilike", dictionary[] = ["i", "like", "gfg"]Output: trueExplanation: The string can be segmented as "i like".Input: s = "
12 min read
Vertex Cover Problem (Dynamic Programming Solution for Tree)A vertex cover of an undirected graph is a subset of its vertices such that for every edge (u, v) of the graph, either ‘u’ or ‘v’ is in vertex cover. Although the name is Vertex Cover, the set covers all edges of the given graph. The problem to find minimum size vertex cover of a graph is NP complet
15+ min read
Tile Stacking ProblemGiven integers n (the height of the tower), m (the maximum size of tiles available), and k (the maximum number of times each tile size can be used), the task is to calculate the number of distinct stable towers of height n that can be built. Note:A stable tower consists of exactly n tiles, each stac
15+ min read
Box Stacking ProblemGiven three arrays height[], width[], and length[] of size n, where height[i], width[i], and length[i] represent the dimensions of a box. The task is to create a stack of boxes that is as tall as possible, but we can only stack a box on top of another box if the dimensions of the 2-D base of the low
15+ min read
Partition a Set into Two Subsets of Equal SumGiven an array arr[], the task is to check if it can be partitioned into two parts such that the sum of elements in both parts is the same.Note: Each element is present in either the first subset or the second subset, but not in both.Examples: Input: arr[] = [1, 5, 11, 5]Output: true Explanation: Th
15+ min read
Travelling Salesman Problem using Dynamic ProgrammingGiven a 2d matrix cost[][] of size n where cost[i][j] denotes the cost of moving from city i to city j. The task is to complete a tour from city 0 (0-based index) to all other cities such that we visit each city exactly once and then at the end come back to city 0 at minimum cost.Note the difference
15 min read
Longest Palindromic Subsequence (LPS)Given a string s, find the length of the Longest Palindromic Subsequence in it. Note: The Longest Palindromic Subsequence (LPS) is the maximum-length subsequence of a given string that is also a Palindrome. Longest Palindromic SubsequenceExamples:Input: s = "bbabcbcab"Output: 7Explanation: Subsequen
15+ min read
Longest Common Increasing Subsequence (LCS + LIS)Given two arrays, a[] and b[], find the length of the longest common increasing subsequence(LCIS). LCIS refers to a subsequence that is present in both arrays and strictly increases.Prerequisites: LCS, LIS.Examples:Input: a[] = [3, 4, 9, 1], b[] = [5, 3, 8, 9, 10, 2, 1]Output: 2Explanation: The long
15+ min read
Find all distinct subset (or subsequence) sums of an arrayGiven an array arr[] of size n, the task is to find a distinct sum that can be generated from the subsets of the given sets and return them in increasing order. It is given that the sum of array elements is small.Examples: Input: arr[] = [1, 2]Output: [0, 1, 2, 3]Explanation: Four distinct sums can
15+ min read
Weighted Job SchedulingGiven a 2D array jobs[][] of order n*3, where each element jobs[i] defines start time, end time, and the profit associated with the job. The task is to find the maximum profit you can take such that there are no two jobs with overlapping time ranges.Note: If the job ends at time X, it is allowed to
15+ min read
Count Derangements (Permutation such that no element appears in its original position)A Derangement is a permutation of n elements, such that no element appears in its original position. For example, a derangement of [0, 1, 2, 3] is [2, 3, 1, 0].Given a number n, find the total number of Derangements of a set of n elements.Examples : Input: n = 2Output: 1Explanation: For two balls [1
12 min read
Minimum insertions to form a palindromeGiven a string s, the task is to find the minimum number of characters to be inserted to convert it to a palindrome.Examples:Input: s = "geeks"Output: 3Explanation: "skgeegks" is a palindromic string, which requires 3 insertions.Input: s= "abcd"Output: 3Explanation: "abcdcba" is a palindromic string
15+ min read
Ways to arrange Balls such that adjacent balls are of different typesThere are 'p' balls of type P, 'q' balls of type Q and 'r' balls of type R. Using the balls we want to create a straight line such that no two balls of the same type are adjacent.Examples : Input: p = 1, q = 1, r = 0Output: 2Explanation: There are only two arrangements PQ and QPInput: p = 1, q = 1,
15+ min read