Skip to content

Tabulation vs Memoization

Dynamic Programming (DP) Introduction

Last Updated : 24 Dec, 2024

Dynamic Programming is a commonly used algorithmic technique used to optimize recursive solutions when same subproblems are called again.

The core idea behind DP is to store solutions to subproblems so that each is solved only once.
To solve DP problems, we first write a recursive solution in a way that there are overlapping subproblems in the recursion tree (the recursive function is called with the same parameters multiple times)
To make sure that a recursive value is computed only once (to improve time taken by algorithm), we store results of the recursive calls.
There are two ways to store the results, one is top down (or memoization) and other is bottom up (or tabulation).

When to Use Dynamic Programming (DP)?

Dynamic programming is used for solving problems that consists of the following characteristics:

1. Optimal Substructure:

The property Optimal substructure means that we use the optimal results of subproblems to achieve the optimal result of the bigger problem.

Example:

Consider the problem of finding the minimum cost path in a weighted graph from a source node to a destination node. We can break this problem down into smaller subproblems:
Find the minimum cost path from the source node to each intermediate node.
Find the minimum cost path from each intermediate node to the destination node.
The solution to the larger problem (finding the minimum cost path from the source node to the destination node) can be constructed from the solutions to these smaller subproblems.

2. Overlapping Subproblems:

The same subproblems are solved repeatedly in different parts of the problem refer to Overlapping Subproblems Property in Dynamic Programming.

Example:

Consider the problem of computing the Fibonacci series. To compute the Fibonacci number at index n, we need to compute the Fibonacci numbers at indices n-1 and n-2. This means that the subproblem of computing the Fibonacci number at index n-2 is used twice (note that the call for n - 1 will make two calls, one for n-2 and other for n-3) in the solution to the larger problem of computing the Fibonacci number at index n.
You may notice overlapping subproblems highlighted in the second recursion tree for Nth Fibonacci diagram shown below.

Approaches of Dynamic Programming (DP)

Dynamic programming can be achieved using two approaches:

1. Top-Down Approach (Memoization):

In the top-down approach, also known as memoization, we keep the solution recursive and add a memoization table to avoid repeated calls of same subproblems.

Before making any recursive call, we first check if the memoization table already has solution for it.
After the recursive call is over, we store the solution in the memoization table.

2. Bottom-Up Approach (Tabulation):

In the bottom-up approach, also known as tabulation, we start with the smallest subproblems and gradually build up to the final solution.

We write an iterative solution (avoid recursion overhead) and build the solution in bottom-up manner.
We use a dp table where we first fill the solution for base cases and then fill the remaining entries of the table using recursive formula.
We only use recursive formula on table entries and do not make recursive calls.

Dynamic-Programming

Please refer Tabulation vs Memoization for the detailed differences.

Example of Dynamic Programming (DP)

Example 1: Consider the problem of finding the Fibonacci sequence:

Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

Brute Force Approach: To find the nth Fibonacci number using a brute force approach, you would simply add the (n-1)th and (n-2)th Fibonacci numbers.

C++

// C++ program to find  // fibonacci number using recursion. #include <bits/stdc++.h> using namespace std;  // Function to find nth fibonacci number int fib(int n) {     if (n <= 1) {         return n;     }      return fib(n - 1) + fib(n - 2); }  int main() {     int n = 5;     cout << fib(n);     return 0; }

C

// C program to find  // fibonacci number using recursion. #include <stdio.h>  // Function to find nth fibonacci number int fib(int n) {     if (n <= 1) {         return n;     }     return fib(n - 1) + fib(n - 2); }  int main() {     int n = 5;     printf("%d", fib(n));     return 0; }

Java

// Java program to find  // fibonacci number using recursion. class GfG {        // Function to find nth fibonacci number     static int fib(int n) {         if (n <= 1) {             return n;         }         return fib(n - 1) + fib(n - 2);     }      public static void main(String[] args) {         int n = 5;         System.out.println(fib(n));     } }

Python

# Python program to find  # fibonacci number using recursion.  # Function to find nth fibonacci number def fib(n):     if n <= 1:         return n     return fib(n - 1) + fib(n - 2)  if __name__ == "__main__":     n = 5     print(fib(n))

C#

// C# program to find  // fibonacci number using recursion. using System;  class GfG {        // Function to find nth fibonacci number     static int fib(int n) {         if (n <= 1) {             return n;         }         return fib(n - 1) + fib(n - 2);     }      static void Main(string[] args) {         int n = 5;         Console.WriteLine(fib(n));     } }

JavaScript

// JavaScript program to find  // fibonacci number using recursion.  // Function to find nth fibonacci number function fib(n) {     if (n <= 1) {         return n;     }     return fib(n - 1) + fib(n - 2); }  //driver code let n = 5; console.log(fib(n));

Output

Below is the recursion tree of the above recursive solution.

fibonaci

The time complexity of the above approach is exponential and upper bounded by O(2ⁿ) as we make two recursive calls in every function.

How will Dynamic Programming (DP) Work?

Let’s us now see the above recursion tree with overlapping subproblems highlighted with same color. We can clearly see that that recursive solution is doing a lot work again and again which is causing the time complexity to be exponential. Imagine time taken for computing a large Fibonacci number.

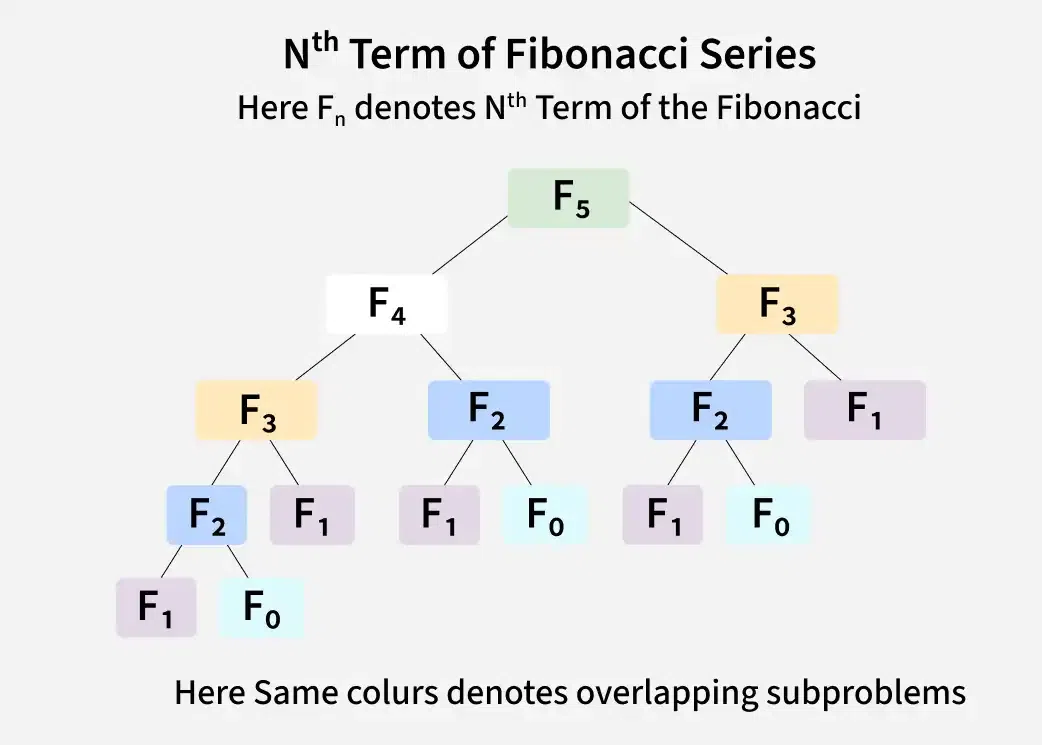
Identify Subproblems: Divide the main problem into smaller, independent subproblems, i.e., F(n-1) and F(n-2)
Store Solutions: Solve each subproblem and store the solution in a table or array so that we do not have to recompute the same again.
Build Up Solutions: Use the stored solutions to build up the solution to the main problem. For F(n), look up F(n-1) and F(n-2) in the table and add them.
Avoid Recomputation: By storing solutions, DP ensures that each subproblem (for example, F(2)) is solved only once, reducing computation time.

Using Memoization Approach - O(n) Time and O(n) Space

To achieve this in our example we simply take an memo array initialized to -1. As we make a recursive call, we first check if the value stored in the memo array corresponding to that position is -1. The value -1 indicates that we haven't calculated it yet and have to recursively compute it. The output must be stored in the memo array so that, next time, if the same value is encountered, it can be directly used from the memo array.

C++

// C++ program to find // fibonacci number using memoization. #include <iostream> #include <vector> using namespace std;  int fibRec(int n, vector<int> &memo) {        // Base case     if (n <= 1) {         return n;     }      // To check if output already exists     if (memo[n] != -1) {         return memo[n];     }      // Calculate and save output for future use     memo[n] = fibRec(n - 1, memo) + fibRec(n - 2, memo);      return memo[n]; }  int fib(int n) {     vector<int> memo(n + 1, -1);     return fibRec(n, memo); }  int main() {     int n = 5;     cout << fib(n);     return 0; }

Java

// Java program to find // fibonacci number using memoization. import java.util.Arrays;  class GfG {      static int fibRec(int n, int[] memo) {          // Base case         if (n <= 1) {             return n;         }          // To check if output already exists         if (memo[n] != -1) {             return memo[n];         }          // Calculate and save output for future use         memo[n] = fibRec(n - 1, memo) + fibRec(n - 2, memo);          return memo[n];     }      static int fib(int n) {         int[] memo = new int[n + 1];         Arrays.fill(memo, -1);         return fibRec(n, memo);     }      public static void main(String[] args) {         int n = 5;         System.out.println(fib(n));     } }

Python

# Python program to find # fibonacci number using memoization. def fibRec(n, memo):        # Base case     if n <= 1:         return n      # To check if output already exists     if memo[n] != -1:         return memo[n]      # Calculate and save output for future use     memo[n] = fibRec(n - 1, memo) + \               fibRec(n - 2, memo)     return memo[n]  def fib(n):     memo = [-1] * (n + 1)     return fibRec(n, memo)  n = 5 print(fib(n))

C#

// C# program to find // fibonacci number using memoization. using System; using System.Collections.Generic;  class GfG {        // Recursive function with memoization     static int FibRec(int n, List<int> memo) {                // Base case         if (n <= 1)         {             return n;         }          // To check if output already exists         if (memo[n] != -1) {             return memo[n];         }          // Calculate and save output for future use         memo[n] = FibRec(n - 1, memo) + FibRec(n - 2, memo);          return memo[n];     }      // Wrapper function to initiate the    	// memoization process     static int Fib(int n) {                // Initialize the memoization array with -1         List<int> memo = new List<int>(new int[n + 1]);         for (int i = 0; i <= n; i++) {             memo[i] = -1;         }         return FibRec(n, memo);     }      static void Main() {         int n = 5;         Console.WriteLine(Fib(n));      } }

JavaScript

// Javascript program to find // fibonacci number using memoization. function fibRec(n, memo) {      // Base case     if (n <= 1) {         return n;     }      // To check if output already exists     if (memo[n] !== -1) {         return memo[n];     }      // Calculate and save output for future use     memo[n] = fibRec(n - 1, memo) +                fibRec(n - 2, memo);      // Returning the final output     return memo[n]; }  function fib(n) {      // Initialize array with -1     const memo = new Array(n + 1).fill(-1);      // Call helper function     return fibRec(n, memo); }  // Driver code const n = 5; console.log(fib(n));

Output

Using Tabulation Approach - O(n) Time and O(n) Space

In this approach, we use an array of size (n + 1), often called dp[], to store Fibonacci numbers. The array is initialized with base values at the appropriate indices, such as dp[0] = 0 and dp[1] = 1. Then, we iteratively calculate Fibonacci values from dp[2] to dp[n] by using the relation dp[i] = dp[i-1] + dp[i-2]. This allows us to efficiently compute Fibonacci numbers in a loop. Finally, the value at dp[n] gives the Fibonacci number for the input n, as each index holds the answer for its corresponding Fibonacci number.

C++

// C++ program to find // fibonacci number using tabulation. #include <iostream> #include <vector> using namespace std;  // Function for calculating the nth Fibonacci number int fibo(int n) {     vector<int> dp(n + 1);      // Storing the independent values in dp     dp[0] = 0;     dp[1] = 1;      // Using the bottom-up approach     for (int i = 2; i <= n; i++) {         dp[i] = dp[i - 1] + dp[i - 2];     }        return dp[n]; }  int main() {     int n = 5;     cout << fibo(n);     return 0; }

C

// C program to find // fibonacci number using tabulation. #include <stdio.h>  // Function for calculating the nth Fibonacci number int fibo(int n) {     int dp[n + 1];      // Storing the independent values in dp     dp[0] = 0;     dp[1] = 1;      // Using the bottom-up approach     for (int i = 2; i <= n; i++) {         dp[i] = dp[i - 1] + dp[i - 2];     }        return dp[n]; }  int main() {     int n = 5;     printf("%d", fibo(n));     return 0; }

Java

// Java program to find // fibonacci number using tabulation. import java.util.Arrays;  // Function for calculating the nth Fibonacci number class GfG {     static int fibo(int n) {         int[] dp = new int[n + 1];          // Storing the independent values in dp         dp[0] = 0;         dp[1] = 1;          // Using the bottom-up approach         for (int i = 2; i <= n; i++) {             dp[i] = dp[i - 1] + dp[i - 2];         }          return dp[n];     }      public static void main(String[] args) {         int n = 5;         System.out.println(fibo(n));     } }

Python

# Python program to find # fibonacci number using tabulation. def fibo(n):     dp = [0] * (n + 1)      # Storing the independent values in dp     dp[0] = 0     dp[1] = 1      # Using the bottom-up approach     for i in range(2, n + 1):         dp[i] = dp[i - 1] + dp[i - 2]          return dp[n]  n = 5 print(fibo(n))

C#

// C# program to find // fibonacci number using tabulation. using System;  class GfG {     static int Fibo(int n) {         int[] dp = new int[n + 1];          // Storing the independent values in dp         dp[0] = 0;         dp[1] = 1;          // Using the bottom-up approach         for (int i = 2; i <= n; i++) {             dp[i] = dp[i - 1] + dp[i - 2];         }                  return dp[n];     }      static void Main() {         int n = 5;         Console.WriteLine(Fibo(n));     } }

JavaScript

// JavaScript program to find // fibonacci number using tabulation.  function fibo(n) {     let dp = new Array(n + 1);      // Storing the independent values in dp     dp[0] = 0;     dp[1] = 1;      // Using the bottom-up approach     for (let i = 2; i <= n; i++) {         dp[i] = dp[i - 1] + dp[i - 2];     }          return dp[n]; }  //driver code let n = 5; console.log(fibo(n));

Output

Using Space Optimised Approach - O(n) Time and O(1) Space

In the above code, we can see that the current state of any fibonacci number depends only on the previous two values. So we do not need to store the whole table of size n+1 but instead of that we can only store the previous two values.

C++

// C++ program to find // fibonacci number using space optimised. #include <iostream> using namespace std;  int fibo(int n) {        int prevPrev, prev, curr;      // Storing the independent values     prevPrev = 0;     prev = 1;     curr = 1;      // Using the bottom-up approach     for (int i = 2; i <= n; i++) {         curr = prev + prevPrev;         prevPrev = prev;         prev = curr;     }      return curr; }  int main() {     int n = 5;     cout << fibo(n);     return 0; }

C

// C program to find // fibonacci number using space optimised. #include <stdio.h>  int fibo(int n) {     int prevPrev, prev, curr;      // Storing the independent values     prevPrev = 0;     prev = 1;     curr = 1;      // Using the bottom-up approach     for (int i = 2; i <= n; i++) {         curr = prev + prevPrev;         prevPrev = prev;         prev = curr;     }      return curr; }  int main() {     int n = 5;     printf("%d", fibo(n));     return 0; }

Java

// Java program to find // fibonacci number using space optimised. class GfG {     static int fibo(int n) {         int prevPrev, prev, curr;          // Storing the independent values         prevPrev = 0;         prev = 1;         curr = 1;          // Using the bottom-up approach         for (int i = 2; i <= n; i++) {             curr = prev + prevPrev;             prevPrev = prev;             prev = curr;         }          return curr;     }      public static void main(String[] args) {         int n = 5;         System.out.println(fibo(n));     } }

Python

# Python program to find # fibonacci number using space optimised. def fibo(n):     prevPrev, prev, curr = 0, 1, 1      # Using the bottom-up approach     for i in range(2, n + 1):         curr = prev + prevPrev         prevPrev = prev         prev = curr      return curr  n = 5 print(fibo(n))

C#

// C# program to find // fibonacci number using space optimised. using System;  class GfG {     static int Fibo(int n) {         int prevPrev = 0, prev = 1, curr = 1;          // Using the bottom-up approach         for (int i = 2; i <= n; i++) {             curr = prev + prevPrev;             prevPrev = prev;             prev = curr;         }          return curr;     }      static void Main() {         int n = 5;         Console.WriteLine(Fibo(n));     } }

JavaScript

// Javascript program to find // fibonacci number using space optimised. function fibo(n) {     let prevPrev = 0, prev = 1, curr = 1;      // Using the bottom-up approach     for (let i = 2; i <= n; i++) {         curr = prev + prevPrev;         prevPrev = prev;         prev = curr;     }      return curr; }  let n = 5; console.log(fibo(n));

Output

Common Algorithms that Use DP:

Longest Common Subsequence (LCS): This is used in day to day life to find difference between two files (diff utility)
Edit Distance : Checks how close to strings are. Can we be useful in implementing Google's did you mean type feature.
Longest Increasing Subsequence : There are plenty of variations of this problem that arise in real world.
Bellman–Ford Shortest Path: Finds the shortest path from a given source to all other vertices.
Floyd Warshall : Finds shortest path from every pair of vertices.
Knapsack Problem: Determines the maximum value of items that can be placed in a knapsack with a given capacity.
Matrix Chain Multiplication: Optimizes the order of matrix multiplication to minimize the number of operations.
Fibonacci Sequence: Calculates the nth Fibonacci number.

Advantages of Dynamic Programming (DP)

Dynamic programming has a wide range of advantages, including:

Avoids recomputing the same subproblems multiple times, leading to significant time savings.
Ensures that the optimal solution is found by considering all possible combinations.

Applications of Dynamic Programming (DP)

Dynamic programming has a wide range of applications, including:

Optimization: Knapsack problem, shortest path problem, maximum subarray problem
Computer Science: Longest common subsequence, edit distance, string matching
Operations Research: Inventory management, scheduling, resource allocation

Characteristics of Dynamic Programming Algorithm

For any problem, if there is a simple recursive solution and a recursion tree has same recursive calls multiple times (or overlapping subproblems), we use DP.

Tabulation vs Memoization

K

kartik

Improve

Article Tags :

Practice Tags :

Dynamic Programming

Similar Reads

Dynamic Programming or DP

Dynamic Programming is an algorithmic technique with the following properties.It is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for the same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of

What is Memoization? A Complete Tutorial

In this tutorial, we will dive into memoization, a powerful optimization technique that can drastically improve the performance of certain algorithms. Memoization helps by storing the results of expensive function calls and reusing them when the same inputs occur again. This avoids redundant calcula

Dynamic Programming (DP) Introduction

Dynamic Programming is a commonly used algorithmic technique used to optimize recursive solutions when same subproblems are called again.The core idea behind DP is to store solutions to subproblems so that each is solved only once. To solve DP problems, we first write a recursive solution in a way t

Tabulation vs Memoization

Tabulation and memoization are two techniques used to implement dynamic programming. Both techniques are used when there are overlapping subproblems (the same subproblem is executed multiple times). Below is an overview of two approaches.Memoization:Top-down approachStores the results of function ca

Optimal Substructure Property in Dynamic Programming | DP-2

The following are the two main properties of a problem that suggest that the given problem can be solved using Dynamic programming: 1) Overlapping Subproblems 2) Optimal Substructure We have already discussed the Overlapping Subproblem property. Let us discuss the Optimal Substructure property here.

Overlapping Subproblems Property in Dynamic Programming | DP-1

Dynamic Programming is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems using recursion and storing the results of subproblems to avoid computing the same results again. Following are the two main properties of a problem that suggests that the given problem

Steps to solve a Dynamic Programming Problem

Steps to solve a Dynamic programming problem:Identify if it is a Dynamic programming problem.Decide a state expression with the Least parameters.Formulate state and transition relationship.Apply tabulation or memorization.Step 1: How to classify a problem as a Dynamic Programming Problem? Typically,