Convex Hull Algorithm

Last Updated : 08 Aug, 2024

The Convex Hull Algorithm is used to find the convex hull of a set of points in computational geometry. The convex hull is the smallest convex set that encloses all the points, forming a convex polygon. This algorithm is important in various applications such as image processing, route planning, and object modeling.

What is Convex Hull?

The convex hull of a set of points in a Euclidean space is the smallest convex polygon that encloses all of the points. In two dimensions (2D), the convex hull is a convex polygon, and in three dimensions (3D), it is a convex polyhedron.

The below image shows a 2-D convex polygon:

Table of Content

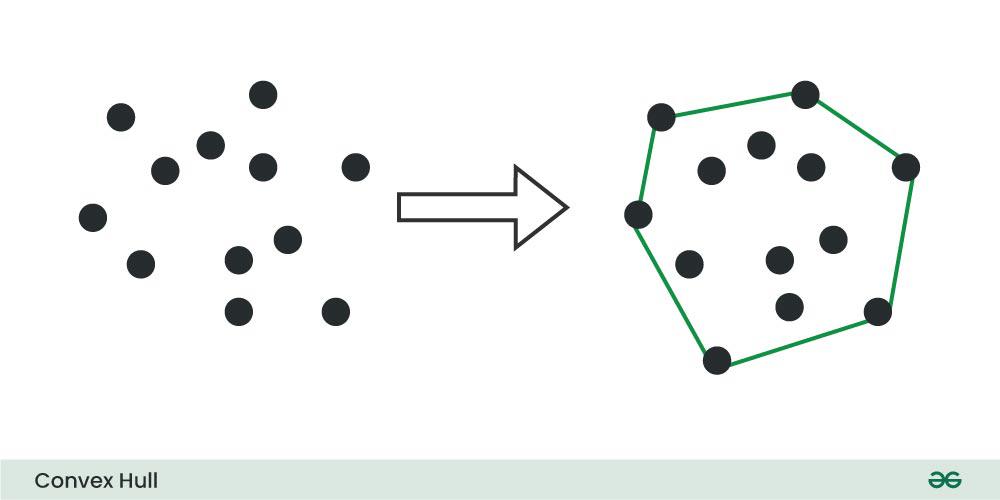
Problem Statement: Given an array of coordinates {x, y} on a 2-D plain, your task is to print the set of coordinates that form the convex hull.

Examples:

Input: points[] = {(0, 0), (0, 4), (-4, 0), (5, 0), (0, -6), (1, 0)};
Output: (-4, 0), (5, 0), (0, -6), (0, 4)
Input: points_list = {{1, 2}, {3, 1}, {5, 6}}
Output: {{1, 2}, {3, 1}, {5, 6}}

Convex Hull using Divide and Conquer Algorithm:

Pre-requisite: Tangents between two convex polygons

Algorithm: Given the set of points for which we have to find the convex hull. Suppose we know the convex hull of the left half points and the right half points, then the problem now is to merge these two convex hulls and determine the convex hull for the complete set.

This can be done by finding the upper and lower tangent to the right and left convex hulls. This is illustrated here Tangents between two convex polygons Let the left convex hull be a and the right convex hull be b.
Then the lower and upper tangents are named as 1 and 2 respectively, as shown in the figure. Then the red outline shows the final convex hull.

Final-Convex-Hull

Now the problem remains, how to find the convex hull for the left and right half. Now recursion comes into the picture, we divide the set of points until the number of points in the set is very small, say 5, and we can find the convex hull for these points by the brute algorithm.
The merging of these halves would result in the convex hull for the complete set of points. Note: We have used the brute algorithm to find the convex hull for a small number of points and it has a time complexity of O(N^3).
But some people suggest the following, the convex hull for 3 or fewer points is the complete set of points. This is correct but the problem comes when we try to merge a left convex hull of 2 points and right convex hull of 3 points, then the program gets trapped in an infinite loop in some special cases.
So, to get rid of this problem I directly found the convex hull for 5 or fewer points by O(N^3) algorithm, which is somewhat greater but does not affect the overall complexity of the algorithm.

Convex Hull using Jarvis’ Algorithm or Wrapping:

Pre-requisite: How to check if two given line segments intersect?

The idea of Jarvis’s Algorithm is simple, we start from the leftmost point (or point with minimum x coordinate value) and we keep wrapping points in counterclockwise direction.
The big question is, given a point p as current point, how to find the next point in output?
The idea is to use orientation() here. Next point is selected as the point that beats all other points at counterclockwise orientation, i.e., next point is q if for any other point r, we have “orientation(p, q, r) = counterclockwise”.

Algorithm:

Initialize p as leftmost point.
Do following while we don’t come back to the first (or leftmost) point.
- The next point q is the point, such that the triplet (p, q, r) is counter clockwise for any other point r. To find this, we simply initialize q as next point, then we traverse through all points. For any point i, if i is more counter clockwise, i.e., orientation(p, i, q) is counter clockwise, then we update q as i. Our final value of q is going to be the most counter clockwise point.
- next[p] = q (Store q as next of p in the output convex hull).
- p = q (Set p as q for next iteration).

Convex-Hull-using-Jarvis-Algorithm-or-Wrapping

Convex Hull using Graham Scan:

Pre-requisite: How to check if two given line segments intersect?

Algorithm: Let points[0..n-1] be the input array. Then the algorithm can be divided into two phases:

Phase 1 (Sort points): We first find the bottom-most point. The idea is to pre-process points be sorting them with respect to the bottom-most point. Once the points are sorted, they form a simple closed path (See the following diagram).

Convex-Hull-using-Graham-Scan-1

What should be the sorting criteria? computation of actual angles would be inefficient since trigonometric functions are not simple to evaluate. The idea is to use the orientation to compare angles without actually computing them (See the compare() function below)

Phase 2 (Accept or Reject Points): Once we have the closed path, the next step is to traverse the path and remove concave points on this path. How to decide which point to remove and which to keep? Again, orientation helps here. The first two points in sorted array are always part of Convex Hull. For remaining points, we keep track of recent three points, and find the angle formed by them. Let the three points be prev(p), curr(c) and next(n). If orientation of these points (considering them in same order) is not counterclockwise, we discard c, otherwise we keep it. Following diagram shows step by step process of this phase.

Convex-Hull-using-Graham-Scan-2

Convex Hull | Monotone Chain Algorithm:

Monotone chain algorithm constructs the convex hull in O(n * log(n)) time. We have to sort the points first and then calculate the upper and lower hulls in O(n) time. The points will be sorted with respect to x-coordinates (with respect to y-coordinates in case of a tie in x-coordinates), we will then find the left most point and then try to rotate in clockwise direction and find the next point and then repeat the step until we reach the rightmost point and then again rotate in the clockwise direction and find the lower hull.

Quickhull Algorithm for Convex Hull:

The QuickHull algorithm is a Divide and Conquer algorithm similar to QuickSort. Let a[0…n-1] be the input array of points. Following are the steps for finding the convex hull of these points.

Algorithm:

Find the point with minimum x-coordinate lets say, min_x and similarly the point with maximum x-coordinate, max_x.
Make a line joining these two points, say L. This line will divide the whole set into two parts. Take both the parts one by one and proceed further.
For a part, find the point P with maximum distance from the line L. P forms a triangle with the points min_x, max_x. It is clear that the points residing inside this triangle can never be the part of convex hull.
The above step divides the problem into two sub-problems (solved recursively). Now the line joining the points P and min_x and the line joining the points P and max_x are new lines and the points residing outside the triangle is the set of points. Repeat point no. 3 till there no point left with the line. Add the end points of this point to the convex hull.

Complexity Analysis for Convex Hull Algorithm:

The below table enlists the time complexities of the above mentioned convex hull algorithms.
where, N denotes the total number of given points.

Convex Hull Algorithm	Time Complexity
Convex Hull using Divide and Conquer Algorithm	O(N*log N)
Convex Hull using Jarvis’ Algorithm or Wrapping	O(N²)
Convex Hull using Graham Scan	O(N*logN)
Convex Hull using Monotone chain algorithm	O(N*log(N))
Convex Hull using Quickhull Algorithm	The analysis is similar to Quick Sort. On average, we get time complexity as O(N*log N), but in worst case, it can become O(N²)

Problems on Convex Hull:

Problem links
Dynamic Convex hull \| Adding Points to an Existing Convex Hull
Deleting points from Convex Hull
Perimeter of Convex hull for a given set of points
Check if the given point lies inside given N points of a Convex Polygon
Tangents between two Convex Polygons
Check if given polygon is a convex polygon or not
Check whether two convex regular polygon have same center or not
Minimum Enclosing Circle

Convex Hull using Divide and Conquer Algorithm

vaibhav_gfg

Improve

Article Tags :

Practice Tags :

Divide and Conquer