Consensus Theorem in Digital Logic
Last Updated : 01 May, 2025
The Consensus Theorem is a simplification rule in Boolean algebra that helps in minimizing logical expressions by eliminating redundant terms. That is why it is also known as Redundancy Theorem.
To apply this theorem, the Boolean expression must meet following conditions:
- The expression should consist of three terms (like XY + X'Z + YZ).
- One term should contain a variable (e.g. X) and another term should have the complemented form of that variable (e.g. X').
- Third term should include all the variables from both terms except the variables mentioned in second point (such as YZ in XY + X'Z + YZ).
The Consensus Theorem states that:
In a Boolean expression consisting of three terms where one term contains a variable, another contains the complement of that variable, and the third term consists of the remaining non-complemented parts from the first two terms, this third term is redundant and can be eliminated without affecting the logical equivalence of the expression.
The theorem applies in both sum-of-products and product-of-sums forms:
- Sum-of-Products (SOP) Form
AB + A'C + BC = AB + A'C
- Product-of-Sums (POS) Form
(A + B)(A' + C)(B + C) = (A + B)(A' + C)
Here, A' means the complement (NOT) of A. After applying this theorem we can only take those terms which contains the complemented variable. The theorem helps eliminate the redundant term BC or (B + C) in the Boolean expression. The term BC or (B + C) does not affect the final result and can be removed to simplify the equation.
Proof of the Consensus Theorem
We prove the SOP form step by step:
- Start with the left-hand side:
AB + A'C + BC
AB + A'C + BC = AB + A'C + BC(A + A') (since A + A' = 1)
= AB + A'C + ABC + A'BC
- Rearrange terms (Commutative Law):
= AB + ABC + A'C + A'BC
- Factor out common terms (Absorption Law):
= AB + ABC + A'C + A'BC
=AB(1 + C) + A'C(1 +B)
= AB + A'C (since 1 + C = 1 and 1 + B = 1)
AB + A'C + BC = AB + A'C
Thus, the term BC is not needed.
Why is the Consensus Theorem Important
- It simplifies Boolean expressions and makes logic circuits simpler.
- Fewer logic gates mean lower cost and power consumption.
- It is useful in designing efficient digital circuits.
Solved Examples on Consensus Theorem
Example 1:
F = AB + BC' + AC
Here, we have three variables A, B and C and all are repeated twice. The variable C is present in complemented form. So, all the conditions are satisfied for applying this theorem.

After applying Redundancy theorem we can write only the terms containing complemented variables (i.e, C) and omit the Redundancy term i.e., AB.
.'. F = BC' + AC
Example 2:
F = (A + B).(A' + C).(B + C)
Three variables are present and all are repeated twice. The variable A is present in complemented form. Thus, all the three conditions of this theorem is satisfied.
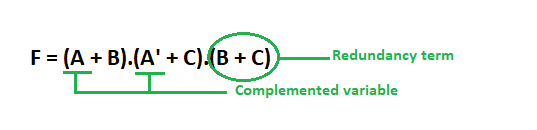
After applying Redundancy theorem we can write only the terms containing complemented variables (i.e, A) and omit the Redundancy term i.e., (B + C).
.'. F = (A + B).(A' + C)
Consider the following equation:
Y = AB + A'C + BC
The third product term BC is a redundant consensus term. If A switches from 1 to 0 while B=1 and C=1, Y remains 1. During the transition of signal A in logic gates, both the first and second term may be 0 momentarily. The third term prevents a glitch since its value of 1 in this case is not affected by the transition of signal A. Thus. it is important to remove Logic Redundancy because it causes unnecessary network complexity and raises the cost of implementation. So, in this way we can minimize a Boolean expression to solve it.
Applications of the Consensus Theorem
- It reducing logic circuits to fewer gates.
- It helps in Boolean function minimization.
- It helps optimize logic circuits in CPUs and other components.
What is the Transposition Theorem?
The Transposition Theorem states that in a Boolean function:
(A + B)(A' + C) = AC + A'B
This theorem helps in circuit design and simplification by showing an alternative way to express a Boolean function.
Similar Reads
Introduction of Logic Gates In Boolean Algebra, there are three basic operations, +,\:.\:,\:^\prime which are analogous to disjunction, conjunction, and negation in propositional logic . Each of these operations has a corresponding logic gate. Apart from these, there are a few other logic gates as well. It was invented by Geor
9 min read
Properties of Boolean Algebra The Boolean Algebra uses sets of rules for analyzing digital gates and circuits. In this article, we will be going through the Properties or Laws of the Boolean algebra. So first we will start our article by defining what are the properties of Boolean Algebra, and then we will go through what are Bo
7 min read
Minimization of Boolean Functions Boolean functions are used to represent logical expressions in terms of sum of minterms or product of maxterms. Number of these literals (minterms or maxterms) increases as the complexity of the digital circuit increases. This can lead to large and inefficient circuits. By minimizing Boolean functio
4 min read
Representation of Boolean Functions Boolean functions are expressions involving Boolean variables and operators, such as AND, OR, and NOT. These functions are fundamental in digital logic design, computer science, and engineering.Table of ContentWhat are Boolean Functions?Definition of Boolean FunctionsRepresentation of Boolean Functi
10 min read
Canonical and Standard Form Canonical Form - In Boolean algebra, the Boolean function can be expressed as Canonical Disjunctive Normal Form known as minterm and some are expressed as Canonical Conjunctive Normal Form known as maxterm. In Minterm, we look for the functions where the output results in "1" while in Maxterm we loo
6 min read
Functional Completeness in Digital Logic Functional Completeness is a crucial concept in digital logic design. A set of logical operators is functionally complete if it can be used to express any Boolean function. This means that any logical operation, regardless of complexity, can be constructed using only operators from a functionally co
6 min read
Introduction of K-Map (Karnaugh Map) In many digital circuits and practical problems, we need to find expressions with minimum variables. We can minimize Boolean expressions of 3, 4 variables very easily using K-map without using any Boolean algebra theorems. It is a tool which is used in digital logic to simplify boolean expression. I
5 min read
Various Implicants in K-Map An implicant can be defined as a product/minterm term in Sum of Products (SOP) or sum/maxterm term in Product of Sums (POS) of a Boolean function. For example, consider a Boolean function, F = AB + ABC + BC. Implicants are AB, ABC, and BC. There are various implicant in K-Map listed below :Prime Imp
5 min read
PDNF and PCNF in Discrete Mathematics PDNF (Principal Disjunctive Normal Form)It stands for Principal Disjunctive Normal Form. It refers to the Sum of Products, i.e., SOP. For eg. : If P, Q, and R are the variables then (P. Q'. R) + (P' . Q . R) + (P . Q . R') is an example of an expression in PDNF. Here '+' i.e. sum is the main operato
4 min read
Variable Entrant Map (VEM) in Digital Logic K-map is the best manual technique to solve Boolean equations but it becomes difficult to manage when number of variables exceed 5 or 6. So, a technique called Variable Entrant Map (VEM) is used to increase the effective size of k-map. It allows a smaller map to handle large number of variables. Thi
3 min read