Difference between sums of odd level and even level nodes of a Binary Tree
Last Updated : 04 Jan, 2025
Given a Binary Tree, the task is to find the difference between the sum of nodes at the odd level and the sum of nodes at the even level.
Examples:
Input:

Output: -4
Explanation: sum at odd levels – sum at even levels = (1) – (2 + 3) = 1 – 5 = -4
Input:
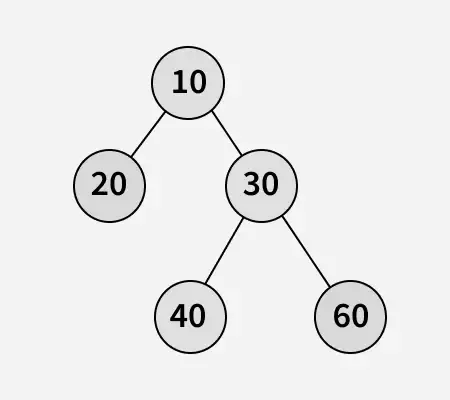
Output: 60
Explanation: Sum at odd levels – Sum at even levels = (10 + 40 + 60) – (20 + 30) = 110 – 50 = 60
Using Recursion – O(n) Time and O(h) Space
The idea is to perform a recursive traversal of the binary tree while keeping track of the current level of each node. At each node, we check if the level is odd or even and add the node’s data to the respective sum. The recursion continues for both the left and right children, with the level being incremented by 1 for each level deeper in the tree. Finally, the difference between the odd level sum and the even level sum is returned.
C++ // C++ program to find the difference between // sums of odd and even level in a Binary tree // using Recursion #include <bits/stdc++.h> using namespace std; class Node { public: int data; Node *left, *right; Node(int x) { data = x; left = nullptr; right = nullptr; } }; void getLevelDiffHelper(Node* root, int level, int& oddSum, int& evenSum) { // Base case: If the node is nullptr, return if (root == nullptr) { return; } // Add to oddSum or evenSum based on the level if (level % 2 != 0) { oddSum += root->data; } else { evenSum += root->data; } // Recur for left and right children with // incremented level getLevelDiffHelper(root->left, level + 1, oddSum, evenSum); getLevelDiffHelper(root->right, level + 1, oddSum, evenSum); } int getLevelDiff(Node* root) { // Initialize sums for odd and even levels int oddSum = 0, evenSum = 0; // Start the recursion from level 1 getLevelDiffHelper(root, 1, oddSum, evenSum); // Return the difference between odd // and even sums return oddSum - evenSum; } int main() { // Hardcoded input binary tree // 10 // / \ // 20 30 // / \ // 40 60 Node* root = new Node(10); root->left = new Node(20); root->right = new Node(30); root->left->left = new Node(40); root->left->right = new Node(60); cout << getLevelDiff(root) << endl; return 0; } // C program to find the difference between // sums of odd and even level in a Binary tree // using Recursion #include <stdio.h> #include <stdlib.h> struct Node { int data; struct Node* left; struct Node* right; }; // Helper function for getLevelDiff void getLevelDiffHelper(struct Node* root, int level, int* oddSum, int* evenSum) { // Base case: If the node is NULL, return if (root == NULL) { return; } // Add to oddSum or evenSum based on the level if (level % 2 != 0) { *oddSum += root->data; } else { *evenSum += root->data; } // Recur for left and right children with // incremented level getLevelDiffHelper(root->left, level + 1, oddSum, evenSum); getLevelDiffHelper(root->right, level + 1, oddSum, evenSum); } // Function to calculate the difference between // sums of odd and even levels int getLevelDiff(struct Node* root) { // Initialize sums for odd and even levels int oddSum = 0, evenSum = 0; // Start the recursion from level 1 getLevelDiffHelper(root, 1, &oddSum, &evenSum); // Return the difference between odd // and even sums return oddSum - evenSum; } struct Node* createNode(int x) { struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = x; newNode->left = NULL; newNode->right = NULL; return newNode; } int main() { // Hardcoded input binary tree // 10 // / \ // 20 30 // / \ // 40 60 struct Node* root = createNode(10); root->left = createNode(20); root->right = createNode(30); root->left->left = createNode(40); root->left->right = createNode(60); printf("%d\n", getLevelDiff(root)); return 0; } // Java program to find the difference between // sums of odd and even level in a Binary tree // using Recursion import java.util.*; class Node { int data; Node left, right; Node(int x) { data = x; left = null; right = null; } } class GfG { static void getLevelDiffHelper(Node root, int level, int[] oddSum, int[] evenSum) { // Base case: If the node is null, return if (root == null) { return; } // Add to oddSum or evenSum based on the level if (level % 2 != 0) { oddSum[0] += root.data; } else { evenSum[0] += root.data; } // Recur for left and right children with // incremented level getLevelDiffHelper(root.left, level + 1, oddSum, evenSum); getLevelDiffHelper(root.right, level + 1, oddSum, evenSum); } static int getLevelDiff(Node root) { // Initialize sums for odd and even levels int[] oddSum = {0}, evenSum = {0}; // Start the recursion from level 1 getLevelDiffHelper(root, 1, oddSum, evenSum); // Return the difference between odd // and even sums return oddSum[0] - evenSum[0]; } public static void main(String[] args) { // Hardcoded input binary tree // 10 // / \ // 20 30 // / \ // 40 60 Node root = new Node(10); root.left = new Node(20); root.right = new Node(30); root.left.left = new Node(40); root.left.right = new Node(60); System.out.println(getLevelDiff(root)); } } # Python program to find the difference between # sums of odd and even level in a Binary tree # using Recursion class Node: def __init__(self, x): self.data = x self.left = None self.right = None def getLevelDiffHelper(root, level, oddSum, evenSum): # Base case: If the node is None, return if root is None: return # Add to oddSum or evenSum based on the level if level % 2 != 0: oddSum[0] += root.data else: evenSum[0] += root.data # Recur for left and right children with # incremented level getLevelDiffHelper(root.left, level + 1, oddSum, evenSum) getLevelDiffHelper(root.right, level + 1, oddSum, evenSum) def getLevelDiff(root): # Initialize sums for odd and even levels oddSum = [0] evenSum = [0] # Start the recursion from level 1 getLevelDiffHelper(root, 1, oddSum, evenSum) # Return the difference between odd # and even sums return oddSum[0] - evenSum[0] if __name__ == "__main__": # Hardcoded input binary tree # 10 # / \ # 20 30 # / \ # 40 60 root = Node(10) root.left = Node(20) root.right = Node(30) root.left.left = Node(40) root.left.right = Node(60) print(getLevelDiff(root))
// C# program to find the difference between // sums of odd and even level in a Binary tree // using Recursion using System; class Node { public int data; public Node left, right; public Node(int x) { data = x; left = null; right = null; } } class GfG { static void getLevelDiffHelper(Node root, int level, ref int oddSum, ref int evenSum) { // Base case: If the node is null, return if (root == null) { return; } // Add to oddSum or evenSum based on the level if (level % 2 != 0) { oddSum += root.data; } else { evenSum += root.data; } // Recur for left and right children with // incremented level getLevelDiffHelper(root.left, level + 1, ref oddSum, ref evenSum); getLevelDiffHelper(root.right, level + 1, ref oddSum, ref evenSum); } static int getLevelDiff(Node root) { // Initialize sums for odd and even levels int oddSum = 0, evenSum = 0; // Start the recursion from level 1 getLevelDiffHelper(root, 1, ref oddSum, ref evenSum); // Return the difference between odd // and even sums return oddSum - evenSum; } static void Main(string[] args) { // Hardcoded input binary tree // 10 // / \ // 20 30 // / \ // 40 60 Node root = new Node(10); root.left = new Node(20); root.right = new Node(30); root.left.left = new Node(40); root.left.right = new Node(60); Console.WriteLine(getLevelDiff(root)); } } // JavaScript program to find the difference between // sums of odd and even level in a Binary tree // using Recursion class Node { constructor(x) { this.data = x; this.left = null; this.right = null; } } function getLevelDiffHelper(root, level, oddSum, evenSum) { // Base case: If the node is null, return if (root === null) { return; } // Add to oddSum or evenSum based on the level if (level % 2 !== 0) { oddSum.value += root.data; } else { evenSum.value += root.data; } // Recur for left and right children with // incremented level getLevelDiffHelper(root.left, level + 1, oddSum, evenSum); getLevelDiffHelper(root.right, level + 1, oddSum, evenSum); } function getLevelDiff(root) { // Initialize sums for odd and even levels const oddSum = { value: 0 }; const evenSum = { value: 0 }; // Start the recursion from level 1 getLevelDiffHelper(root, 1, oddSum, evenSum); // Return the difference between odd // and even sums return oddSum.value - evenSum.value; } // Hardcoded input binary tree // 10 // / \ // 20 30 // / \ // 40 60 const root = new Node(10); root.left = new Node(20); root.right = new Node(30); root.left.left = new Node(40); root.left.right = new Node(60); console.log(getLevelDiff(root)); Time Complexity: O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once during the recursion.
Auxiliary Space: O(h), where h is height of the binary tree due to the recursion stack, which can go up to the height of the tree in the worst case (for a skewed tree).
Using Level Order Traversal – O(n) Time and O(n) Space
The idea is to use level-order traversal (BFS) to process each node in the tree. We maintain a queue to traverse nodes level by level and use a boolean flag to alternate between odd and even levels. As we visit each node, we add its value to the appropriate sum (either oddSum or evenSum). After processing all nodes, the difference between the odd and even level sums is returned.
C++ // C++ program to find difference between // sums of odd and even level in a tree #include <bits/stdc++.h> using namespace std; class Node { public: int data; Node *left, *right; Node(int x) { data = x; left = nullptr; right = nullptr; } }; int getLevelDiff(Node *root) { // If the tree is empty if (root == nullptr) { return 0; } // Queue for level-order traversal queue<Node *> q; q.push(root); int oddSum = 0, evenSum = 0; bool isOdd = true; while (!q.empty()) { int size = q.size(); for (int i = 0; i < size; i++) { Node *curr = q.front(); q.pop(); // Add to oddSum or evenSum if (isOdd) { oddSum += curr->data; } else { evenSum += curr->data; } // Push left and right children // to the queue if (curr->left) { q.push(curr->left); } if (curr->right) { q.push(curr->right); } } // Toggle odd/even level isOdd = !isOdd; } return oddSum - evenSum; } int main() { // Hardcoded input binary tree // 10 // / \ // 20 30 // / \ // 40 60 Node *root = new Node(10); root->left = new Node(20); root->right = new Node(30); root->left->left = new Node(40); root->left->right = new Node(60); cout << getLevelDiff(root) << endl; return 0; } // Java program to find difference between // sums of odd and even level in a tree import java.io.*; import java.util.*; class Node { int data; Node left, right; Node(int key) { data = key; left = right = null; } } class GfG { static int getLevelDiff(Node root) { if (root == null) return 0; // create a queue for // level order traversal Queue<Node> q = new LinkedList<>(); q.add(root); int level = 0; int evenSum = 0, oddSum = 0; // traverse until the // queue is empty while (q.size() != 0) { int size = q.size(); level++; // traverse for complete level while (size > 0) { Node temp = q.remove(); // check if level no is even or odd and // accordingly update the evenSum or oddSum if (level % 2 == 0) evenSum += temp.data; else oddSum += temp.data; // check for left child if (temp.left != null) q.add(temp.left); // check for right child if (temp.right != null) q.add(temp.right); size--; } } return (oddSum - evenSum); } public static void main(String args[]) { // Create a hard coded tree // 10 // / \ // 20 30 // / \ // 40 60 Node root = new Node(10); root.left = new Node(20); root.right = new Node(30); root.left.left = new Node(40); root.left.right = new Node(60); System.out.println(getLevelDiff(root)); } } # Python program to find difference between # sums of odd and even level in a tree from collections import deque class Node: def __init__(self, x): self.data = x self.left = None self.right = None def getLevelDiff(root): # If the tree is empty if root is None: return 0 # Queue for level-order traversal q = deque() q.append(root) oddSum = 0 evenSum = 0 isOdd = True while q: size = len(q) for i in range(size): curr = q.popleft() # Add to oddSum or evenSum if isOdd: oddSum += curr.data else: evenSum += curr.data # Push left and right children # to the queue if curr.left: q.append(curr.left) if curr.right: q.append(curr.right) # Toggle odd/even level isOdd = not isOdd return oddSum - evenSum if __name__ == "__main__": # Hardcoded input binary tree # 10 # / \ # 20 30 # / \ # 40 60 root = Node(10) root.left = Node(20) root.right = Node(30) root.left.left = Node(40) root.left.right = Node(60) print(getLevelDiff(root))
// C# program to find difference between // sums of odd and even level in a tree using System; using System.Collections.Generic; class Node { public int data; public Node left, right; public Node(int key) { data = key; left = right = null; } } class GfG { static int getLevelDiff(Node root) { if (root == null) return 0; // create a queue for // level order traversal Queue<Node> q = new Queue<Node>(); q.Enqueue(root); int level = 0; int evenSum = 0, oddSum = 0; // traverse until the // queue is empty while (q.Count != 0) { int size = q.Count; level++; // traverse for complete level while (size > 0) { Node temp = q.Dequeue(); // check if level no is even or odd and // accordingly update the evenSum or oddSum if (level % 2 == 0) evenSum += temp.data; else oddSum += temp.data; // check for left child if (temp.left != null) q.Enqueue(temp.left); // check for right child if (temp.right != null) q.Enqueue(temp.right); size--; } } return (oddSum - evenSum); } static void Main(String[] args) { // Create a hard coded tree // 10 // / \ // 20 30 // / \ // 40 60 Node root = new Node(10); root.left = new Node(20); root.right = new Node(30); root.left.left = new Node(40); root.left.right = new Node(60); Console.WriteLine(getLevelDiff(root)); } } // JavaScript program to find the difference between // sums of odd and even levels in a tree class Node { constructor(x) { this.data = x; this.left = null; this.right = null; } } function getLevelDiff(root) { // If the tree is empty if (root === null) { return 0; } // Queue for level-order traversal let q = []; q.push(root); let oddSum = 0, evenSum = 0; let isOdd = true; while (q.length > 0) { let size = q.length; // Process all nodes at the current level for (let i = 0; i < size; i++) { let curr = q.shift(); // Add to oddSum or evenSum if (isOdd) { oddSum += curr.data; } else { evenSum += curr.data; } // Push left and right children to the queue if (curr.left !== null) { q.push(curr.left); } if (curr.right !== null) { q.push(curr.right); } } // Toggle odd/even level isOdd = !isOdd; } return oddSum - evenSum; } // Hardcoded input binary tree // 10 // / \ // 20 30 // / \ // 40 60 let root = new Node(10); root.left = new Node(20); root.right = new Node(30); root.left.left = new Node(40); root.left.right = new Node(60); console.log(getLevelDiff(root)); Time Complexity: O(n), where n is the number of nodes in the binary tree. This is because each node is processed once during the level-order traversal.
Auxiliary Space: O(n), this is due to the space required for the queue, which can hold up to n nodes in the worst case.
Similar Reads
Difference between sums of odd level and even level nodes in an N-ary Tree
Given an N-ary Tree rooted at 1, the task is to find the difference between the sum of nodes at the odd level and the sum of nodes at even level. Examples: Input: 4 / | \ 2 3 -5 / \ / \ -1 3 -2 6Output: 10Explanation:Sum of nodes at even levels = 2 + 3 + (-5) = 0Sum of nodes at odd levels = 4 + (-1)
9 min read
Difference between sum of even and odd valued nodes in a Binary Tree
Given a binary tree, the task is to find the absolute difference between the even valued and the odd valued nodes in a binary tree. Examples: Input: 5 / \ 2 6 / \ \ 1 4 8 / / \ 3 7 9 Output: 5 Explanation: Sum of the odd value nodes is: 5 + 1 + 3 + 7 + 9 = 25 Sum of the even value nodes is: 2 + 6 +
10 min read
Difference between sums of odd position and even position nodes for each level of a Binary Tree
Given a Binary Tree, the task is to find the absolute difference between the sums of odd and even positioned nodes. A node is said to be odd and even positioned if its position in the current level is odd and even respectively. Note that the first element of each row is considered as odd positioned.
8 min read
Difference between odd level and even level leaf sum in given Binary Tree
Given a Binary Tree, the task is to find the difference of the sum of leaf nodes at the odd level and even level of the given tree. Examples: Input: Output: -12Explanation: Following are the operations performed to get the result.odd_level_sum = 0, even_level_sum = 0Level 1: No leaf node, so odd_lev
13 min read
Difference between General tree and Binary tree
General Tree: In the data structure, General tree is a tree in which each node can have either zero or many child nodes. It can not be empty. In general tree, there is no limitation on the degree of a node. The topmost node of a general tree is called the root node. There are many subtrees in a gene
2 min read
Maximum absolute difference between any two level sum in a Binary Tree
Given a Binary Tree having positive and negative nodes, the task is to find the maximum absolute difference of level sum in it. Examples: Input: 4 / \ 2 -5 / \ / \ -1 3 -2 6 Output: 9 Explanation: Sum of all nodes of 0 level is 4 Sum of all nodes of 1 level is -3 Sum of all nodes of 2 level is 6 Hen
10 min read
Difference between sums of odd and even digits
Given a long integer, we need to find if the difference between sum of odd digits and sum of even digits is 0 or not. The indexes start from zero (0 index is for leftmost digit). Examples: Input: 1212112Output: YesExplanation:the odd position element is 2+2+1=5the even position element is 1+1+1+2=5t
3 min read
Sum of leaf nodes at each horizontal level in a binary tree
Given a Binary Tree, the task is to find the sum of leaf nodes at every level of the given tree. Examples: Input: Output:0063012Explanation:Level 1: No leaf node, so sum = 0Level 2: No leaf node, so sum = 0Level 3: One leaf node: 6, so sum = 6 Level 4: Three leaf nodes: 9, 10, 11, so sum = 30Level 5
14 min read
Maximum sum of non-leaf nodes among all levels of the given binary tree
Given a Binary Tree having positive and negative nodes, the task is to find the maximum sum of non-leaf nodes among all levels of the given binary tree. Examples: Input: 4 / \ 2 -5 / \ -1 3 Output: 4 Sum of all non-leaf nodes at 0th level is 4. Sum of all non-leaf nodes at 1st level is 2. Sum of all
9 min read
Find the absolute difference of set bits at even and odd indices of N
Given an integer N, the task is to find the absolute difference of set bits at even and odd indices of number N. (0-based Indexing) Examples: Input: N = 15Output: 0Explanation: The binary representation of 15 is 1111. So, it contains 1 on the 1st and 3rd position and it contains 1 on the 0th and 2nd
5 min read