Congruency is a mathematical term that means two or more objects have the same shape and size or if one is the mirror image of the other.
In this article, we will understand the basic geometric concept of congruency, how they are related, their types, some practical applications of congruency, and solve some problems in trigonometry.
What is Congruency?
Congruency explains the relation between two shapes or geometric figures. It plays an important part in analyzing and understanding the relation between two geometric figures. In Mathematics, if two shapes are mirror images of each other, they are said to be congruent shapes.
Congruency means identical shape and size, be it a line segment, any geometrical shape, or an angle. In other words, if two shapes have corresponding sides and angles equal they are known as congruent shapes. The two shapes can be superimposed on each other, side to side and corresponding angle to angle.
Congruency Definition
Congruency means exactly equal shape and size. If any shape can overlap each other and appear to be similar, is known as congruent. Mathematically, it is represented by ≅ sign.
Significance of Congruency in Mathematics
Congruency holds vital importance in mathematical field. Following are some applications of congruency:
- It helps in analyzing shapes and its properties.
- It is useful in calculating accurate measurements.
- It is used in various trigonometric solutions.
Congruency in Geometry
In geometry, congruency is used to identify similar shapes. Even if a shape is rotated or flipped, the congruent shapes remain same.
By definition, two figures, object or shape are said to be congruent if they have same shape or size as the mirror image of the other. The congruent shape superimpose each other. This simply means that they can be placed completely over each other.
For example, two squares with side 5 cm each are congruent to each other, as they can completely overlap each other. Below is the illustration for the same:

Geometric Concepts Related to Congruency
To understand relationship between shapes and make deductions about their properties,we need to identify congruency in any geometrical shape. Following are some geometrical concepts related to congruency:
- Line Segment: Two lines are congruent and they will have same properties if their length is same.
- Angles: Two angles will be congruent, if they have same measure.
- Circle: Two circles are congruent if they have same diameter.
Overall, in order to find congruency in any geometrical shape, we need to identify them using different parameters, For example in case of polygons, we first match the vertices and then move towards sides and angles to find similarity. Let us discuss more on identifying congruent figures in detail.
Identifying Congruent Figures
Congruent figures do have some differences, but in terms of properties they tend to have same measures which help us in analyzing two shapes accurately. To identify congruent figures in any polygon, we can follow the following steps
Step 1: Check the type of 2-dimensional shape(triangle, hexagon, etc) by counting the number of vertices.
Step 2: Check the length of all sides of the figure.
Step 3: Check the measure of all angles of the figure.
If all the measures of the given figures are same, then the given figures are congruent to each other.
Type of Congruency
Congruency can be of different types depending upon its geometrical shape. Congruency can be defined in line segments with same length, angles with same measure, triangles where sides and angles are equal, circles with same diameter or radius, etc. Depending upon the identification of Congruency, it is divided into three major types.
- Reflectional Congruence
- Rotational Congruence
- Translational Congruence
Reflectional Congruence
Reflectional congruence to a congruency where two figures remain same after flipping through a line of reflection. This congruency involves a reflection, which is a type of transformation where a figure is flipped over a line. Here the two figures are identical after getting reflected across a line of reflection which acts like a line of symmetry.
Two figures that are reflectionally congruent can be overlapped on each other after aligning corresponding vertexes. This property helps in identifying symmetry between two geometrical shapes.
Rotational Congruence
Rotational Congruence refers to the congruency where two shapes become same(congruent) when one is turned around a center point.
In simple terms, two figures are congruent rotationally if one of the figures can be transformed to other figure after a specific number of rotations around a center of rotation. Here, one figure is matched with the other figure by rotating it by a specific angle and direction to make them identical or congruent.
Translational Congruence
Translational congruence involves a translation, where a figure is moved from one location to another without changing its orientation or shape. Here two geometric shapes are congruent if they are translated to a specific direction, both the figures can be overlapped on each other by moving the figure parallel to the direction of the translation.
One important thing in translational congruency is that the orientation remains the same, only the figure is slides in a specific direction without rotating or flipping it.

Congruency in Triangle
Congruent triangles are triangles that are perfect copies of one another. Two triangles are said to be congruent if and only if they can be overlapped with each other completely. Two triangles are said to be congruent if they have equal corresponding angles or sides.
Congruency in Triangles can be identified by the following criteria:
- SSS Criteria: Side-Side-Side
- SAS Criteria: Side-Angle-Side
- ASA Criteria: Angle-Side-Angle
- AAS Criteria: Angle-Angle-Side
- RHS Criteria: Right angle- Hypotenuse-Side
Read more about, Congruence of Triangles.
Two figures which overlap on each other with identical shape and dimension are known as congruent figures. However, Properties and characteristics of congruent figures are different depending upon the figure i.e if the figure is a line segment, an angle, circle or any other polygonal shape.
For instance, in triangles, there are various congruency rules to check if the two triangles are congruent to each other or not.
Some of the properties of congruent figures are explained below:
Congruent Angles and Sides
Two angles are said to be congruent if measure of both figures are exactly equal. Similarly, with sides the length of each side should be equal, in order to be congruent.
Figures like triangle, square and other polygons use this congruency rule to prove congruency between two figures.
Corresponding Parts of Congruent Figures
Corresponding parts of congruent figures refers to the equal sides and angles of two figure, where we can overlap or superimpose one figure on the other.
For example if two triangles ABC and CDA are congruent, it would mean sides AB = CD and BC = DA. Corresponding angles are also equal in congruent figures, which means that angle A,B and C are equal to C, D, and A respectively. Hence, if ABC ≅ CDA, then it means sides and angles are equal accordingly.
Other than angles and sides, other corresponding parts can also be equal in congruent figures. For example, any diagonal in square or in parallelogram will also be equal.
Practical Applications of Congruency
Congruency can be useful in various aspects of life, it plays major role in architecturul design, engineering and mantaining accuracy in measurements, specially in computer graphics and animation. Practical Applications of Congruency also expand to the field of mathematics, where it is used in solving geometric and trignometry problems.
Real-Life Scenarios Involving Congruent Shapes
Our everyday life has so many examples of congruency. Few real- life examples of congruent shapes are:
- Pages of the same book.
- Mobile phones of the same brand and same model
- Two bricks.
- A pair of bangles.
Use of Congruency in Architectural Design
Congruency in architectural Design ensures that fundamental parts of structures, including alignments and measurements fit accurately. These measurements help in maintaing balance and stability of structures. From windows to walls, everything in your house was measured and calculated using the fundamentals of congruency which prevents misalignment and imbalance issues.
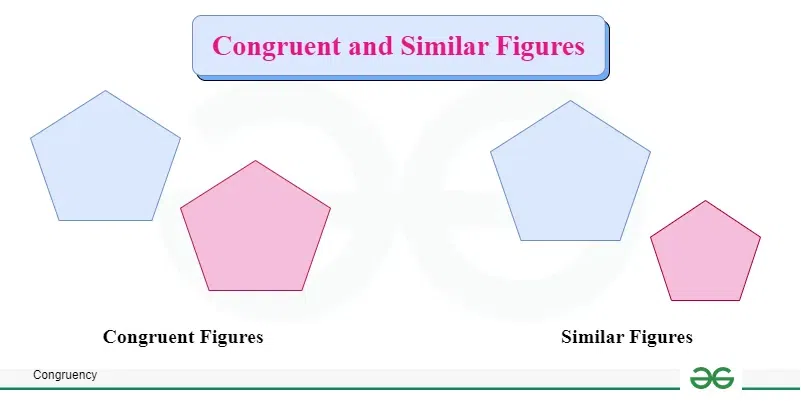
Congruent Figures and Similar figures are different from each other. Congruent figures refers to the figures that have the equal measure of sides and angles. On the other hand, similar figures may have the same shape, but their size may not be the same.
For example, if we have two rectangles they will be similar to each other irrespective of their dimensions, but they will be congruent to each other only when they have the same dimensions.
Below is the representation of the similar and congruent figures:
Read More,
Solving Problems On Congruency
Example 1: ABCD is a square, where AC is diagonal. Prove that triangle, ABC and CDA are congruent?
Solution:
ABCD is a square, so all four sides are congruent. By the properties of square, we also know each angle formed by square is 90°.
Hence we have,
AB = CD
BC = DA
Also, Both Triangles have one side common i.e. AC,
By SSS Congruence theorem. Both triangles, ABC and CDA are congruent.
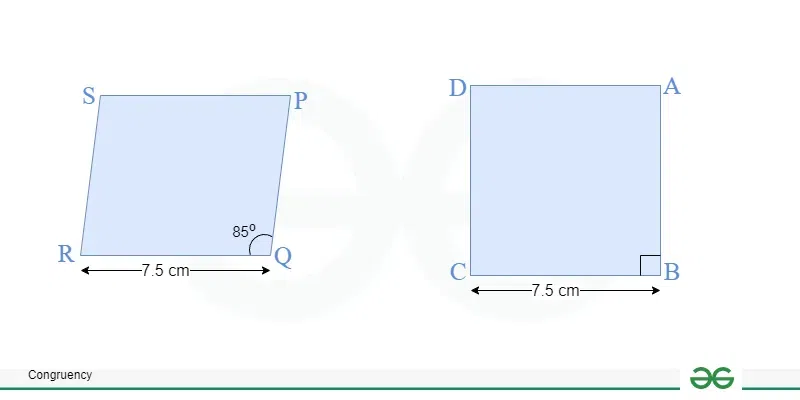
Example 2: Check whether the given Quadrilaterals are congruent or not.
Solution:
In the figure ABCD,
∠ABC = 90
But In PQRS
∠PQR ≠ 90
Hence, the angles of first quadrilateral are not equal to the angles of second quadrilateral. Therefore, the above given figures are not congruent to each other.
Similar Reads
How to use ChatGPT to Create Tutorial Guides Using ChatGPT to create tutorial guides blends AI capabilities with human intelligence in a smooth process. Through the use of ChatGPT's extensive knowledge base and language comprehension, users can create in-depth tutorials on any subject easily. Users first define the topic and create a collectio
8 min read
9th Grade Mathematics Class 9 Math is an important step in learning. It helps you understand useful concepts and solve problems more easily. This guide has all the topics you need to study, along with helpful resources.You’ll find topics like geometry, algebra, and probability, all in one place. Each topic is listed clea
4 min read
Explore GfG Application: Your Gateway to Tech World! Hey Geeks, Imagine a world where learning to code is as easy as pie, and understanding complex concepts feels like a walk in the park. Yes, GeeksforGeeks is the ultimate solution for all kinds of tech solutions you need. And it will be even wonderful to hear that GeeksforGeeks has come up with an ad
4 min read
Coding For Everyone Course By GeekforGeeks Are you a tech geek? Yes! So, you might be interested in diving deep into coding also. But the problem is you're from a non-technical background, Right? Do not worry! GeeksforGeeks has come up with a comprehensive beginner-level course for anyone irrespective of their educational background. In this
2 min read
Grade 10 Maths Grade 10 Maths is an important step in your learning journey. It covers topics that help you build problem-solving skills and understand the world around you better. This article combines all the topics you need to study, with links to helpful resources.You’ll find everything here, from geometry to
4 min read