Exercise 6.4 in Chapter 6 of the Class 8 NCERT Mathematics textbook focuses on applying the concepts of squares and square roots to solve various problems. This exercise builds upon the methods of finding square roots learned earlier in the chapter and introduces students to real-world applications and more complex problems involving these concepts.
Class 8 NCERT Solutions- Exercise 6.4
Question 1. Find the square root of each of the following numbers by Division method.
(i) 2304
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{23} \overline{04}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 23
Divide and get the remainder.
Here, we get 7

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 04
So now the new dividend is 704.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 88 × 8 = 704.
So we choose the new digit as 8.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √2304 = 48
(ii) 4489
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{44} \overline{89}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 44

Divide and get the remainder.
Here, we get 8
Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 89
So now the new dividend is 889.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 127 × 7 = 889.
So we choose the new digit as 7.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √4489 = 67
(iii) 3481
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{34} \overline{81}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 34
Divide and get the remainder.
Here, we get 9

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 81
So now the new dividend is 981.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 109 × 9 = 981.
So we choose the new digit as 9.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √3481 = 59
(iv) 529
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{5} \overline{29}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 5
Divide and get the remainder.
Here, we get 1

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 29
So now the new dividend is 129.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 23 × 3 = 129.
So we choose the new digit as 3.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √529 = 23
(v) 3249
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{32} \overline{49}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 32
Divide and get the remainder.
Here, we get 7

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 49
So now the new dividend is 749.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 107 × 7 = 749.
So we choose the new digit as 7.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √3249 = 57
(vi) 1369
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{13} \overline{69}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 13
Divide and get the remainder.
Here, we get 4

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 69
So now the new dividend is 469.

Step 4: Double the quotient and enter it with a blank on its right.
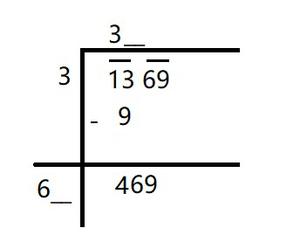
Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 37 × 7 = 469.
So we choose the new digit as 7.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √1369 = 37
(vii) 5776
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{57} \overline{76}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 57
Divide and get the remainder.
Here, we get 8

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 76
So now the new dividend is 876.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 146 × 6 = 876.
So we choose the new digit as 6.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √5776 = 76
(viii) 7921
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{79} \overline{21}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 79
Divide and get the remainder.
Here, we get 15

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 21
So now the new dividend is 1521.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 169 × 9 = 1521.
So we choose the new digit as 9.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √7921 = 89
(ix) 576
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{5} \overline{76}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 5
Divide and get the remainder.
Here, we get 1

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 76
So now the new dividend is 176.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 44 × 4 = 176.
So we choose the new digit as 4.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √576 = 24
(x) 1024
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{10} \overline{24}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 10
Divide and get the remainder.
Here, we get 1

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 24
So now the new dividend is 124.

Step 4: Double the quotient and enter it with a blank on its right.
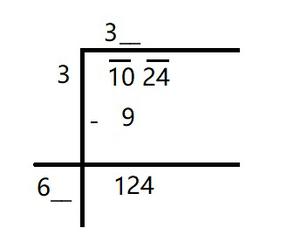
Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 62 × 2 = 124.
So we choose the new digit as 2.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √1024 = 32
(xi) 3136
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{31} \overline{36}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 31
Divide and get the remainder.
Here, we get 6

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 36
So now the new dividend is 636.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 106 × 6 = 636.
So we choose the new digit as 6.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √3136 = 56
(xii) 900
Solution:
Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar.
Thus we have, \overline{9} \overline{00}
Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend.
Here, we have 9
Divide and get the remainder.
Here, we get 0

Step 3: Bring down the remaining number under the next bar to the right of the remainder.
Here, its 0
So now the new dividend is 000.

Step 4: Double the quotient and enter it with a blank on its right.

Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 60 × 0 = 000.
So we choose the new digit as 0.
Get the remainder.

Step 6: Since the remainder is 0 and no digits are left in the given number.
Hence, √900 = 30
Question 2. Find the number of digits in the square root of each of the following numbers (without any calculation).
If n is number of digits in a square number then
Number of digits in the square root = \frac {n}{2} if n is even
and, \frac{n+1}{2} if n is odd.
(i) 64
Solution:
Here, n = 2, which is even
So, number of digits in square root is = \frac {n}{2}
= \frac {2}{2}
= 1
(ii) 144
Solution:
Here, n = 3, which is odd
So, number of digits in square root is = \frac {n+1}{2}
= \frac {4}{2}
= 2
(iii) 4489
Solution:
Here, n = 4, which is even
So, number of digits in square root is = \frac {n}{2}
= \frac {4}{2}
= 2
(iv) 27225
Solution:
Here, n = 5, which is odd
So, number of digits in square root is = \frac {n+1}{2}
= \frac {6}{2}
= 3
(v) 390625
Solution:
Here, n = 6, which is even
So, number of digits in square root is = \frac {n}{2}
= \frac {6}{2}
= 3
Question 3. Find the square root of the following decimal numbers.
(i) 2.56
Solution:
To find the square root of a decimal number we put bars on the integral part of the number in the usual manner. And place bars on the decimal part on every pair of digits beginning with the first decimal place.
We get \overline{2}.\overline{56}

Since the remainder is 0 and no digits are left in the given number.
Hence, √2.56 = 1.6
(ii) 7.29
Solution:
To find the square root of a decimal number we put bars on the integral part of the number in the usual manner. And place bars on the decimal part on every pair of digits beginning with the first decimal place.
We get \overline{7}.\overline{29}

Since the remainder is 0 and no digits are left in the given number.
Hence, √7.29 = 2.7
(iii) 51.84
Solution:
To find the square root of a decimal number we put bars on the integral part of the number in the usual manner. And place bars on the decimal part on every pair of digits beginning with the first decimal place.
We get \overline{51}.\overline{84}

Since the remainder is 0 and no digits are left in the given number.
Hence, √51.84 = 7.2
(iv) 42.25
Solution:
To find the square root of a decimal number we put bars on the integral part of the number in the usual manner. And place bars on the decimal part on every pair of digits beginning with the first decimal place.
We get \overline{42}.\overline{25}

Since the remainder is 0 and no digits are left in the given number.
Hence, √42.25 = 6.5
(v) 31.36
Solution:
To find the square root of a decimal number we put bars on the integral part of the number in the usual manner. And place bars on the decimal part on every pair of digits beginning with the first decimal place.
We get \overline{31}.\overline{36}

Since the remainder is 0 and no digits are left in the given number.
Hence, √31.36 = 5.6
Question 4. Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
Here, remainder is the least required number to be subtracted from the given number to get a perfect square.
(i) 402
Solution:
By following all the steps for obtaining square root, we get

Here remainder is 2
2 is the least required number to be subtracted from 402 to get a perfect square
New number = 402 – 2 = 400
Thus, √400 = 20
(ii) 1989
Solution:
By following all the steps for obtaining square root, we get

Here remainder is 53
53 is the least required number to be subtracted from 1989.
New number = 1989 – 53 = 1936
Thus, √1936 = 44
(iii) 3250
Solution:
By following all the steps for obtaining square root, we get

Here remainder is 1
1 is the least required number to be subtracted from 3250 to get a perfect square.
New number = 3250 – 1 = 3249
Thus, √3249 = 57
(iv) 825
Solution:
By following all the steps for obtaining square root, we get

Here, the remainder is 41
41 is the least required number which can be subtracted from 825 to get a perfect square.
New number = 825 – 41 = 784
Thus, √784 = 28
(v) 4000
Solution:
By following all the steps for obtaining square root, we get

Here, the remainder is 31
31 is the least required number which should be subtracted from 4000 to get a perfect square.
New number = 4000 – 31 = 3969
Thus, √3969 = 63
Question 5. Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525
Solution:
By following all the steps for obtaining square root, we get

Here remainder is 41
It represents that 222 is less than 525.
Next number is 23,
Where, 232 = 529
Hence, the number to be added = 529 – 525 = 4
New number = 525+4 = 529
Thus, √529 = 23
(ii) 1750
Solution:
By following all the steps for obtaining square root, we get

Here the remainder is 69
It represents that 412 is less than in 1750.
The next number is 42
Where, 422 = 1764
Hence, number to be added to 1750 = 1764 – 1750 = 14
New number = 1750 + 14 = 1764
√1764 = 42
(iii) 252
Solution:
By following all the steps for obtaining square root, we get

Here the remainder is 27.
It represents that 152 is less than 252.
The next number is 16
Where,162 = 256
Hence, number to be added to 252 = 256 – 252 = 4
New number = 252 + 4 = 256
and √256 = 16
(iv) 1825
Solution:
By following all the steps for obtaining square root, we get

The remainder is 61.
It represents that 422 is less than in 1825.
Next number is 43
Where, 432 = 1849
Hence, number to be added to 1825 = 1849 – 1825 = 24
New number = 1825 + 24 = 1849
and √1849 = 43
(v) 6412
Solution:
By following all the steps for obtaining square root, we get
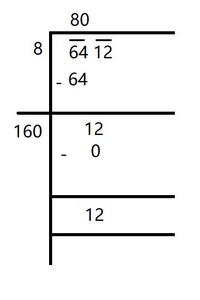
Here, the remainder is 12.
It represents that 802 is less than in 6412.
The next number is 81
Where, 812 = 6561
Hence, the number to be added = 6561 – 6412 = 149
New number = 6412 + 149 = 6561
and √6561 = 81
Question 6. Find the length of the side of a square whose area is 441 m2.
Solution:
Let the side of square be x m.
Area of square = x2
According to the given question,
x2 = 441
x = √441

Hence, the side of square is 21 m.
Question 7. In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC
Solution:
In right triangle ABC
AC2 = AB2 + BC2 [By Pythagoras Theorem]

AC2 = 62 + 82
AC2 = 100
AC = √100

AC = 10 cm
(b) If AC = 13 cm, BC = 5 cm, find AB
Solution:
In right triangle ABC
AC2 = AB2 + BC2 [By Pythagoras Theorem]
132 = AB2 + 52
AB2 = 132 - 52
AB2 = (13+5) (13-5)
AB2 = 18 × 8
AB2 = 144
AB = √144

AB = 12 cm
Question 8. A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this.
Solution:
Let the number of rows and columns be x.
Total number of plants = x2
x2 = 1000
x = √1000

Here the remainder is 39
So the 312 is less than 1000.
Next number is 32
Where, 322 = 1024
Hence the number to be added = 1024 – 1000 = 24
Hence, the minimum number of plants required by him = 24.
Question 9. There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement.
Solution:
Let the number of rows and columns be x.
Total number of plants = x2
x2 = 500
x = √500

Here the remainder is 16
New Number 500 – 16 = 484
and, √484 = 22
Thus, 16 students will be left out in this arrangement.
Conclusion
Chapter 6 of the Class 8 NCERT Mathematics textbook, titled "Squares and Square Roots," provides a comprehensive exploration of these fundamental mathematical concepts. The chapter begins by revisiting the idea of square numbers and their properties, including how to identify perfect squares. It then progresses to the concept of square roots, introducing various methods to calculate them, such as the long division method, estimation, and the method of repeated subtraction. The chapter emphasizes understanding the relationship between squares and square roots, helping students grasp that square root is the inverse operation of squaring.
Similar Reads
NCERT Solutions for Class 8 Maths 2024-25: Chapter Wise Solution PDF Download The NCERT Solutions for Class 8 Maths for the academic year 2024-25 provide comprehensive, chapter-wise solutions to all the problems in the Class 8 Maths textbook. These solutions are designed to help students understand concepts better and excel in their studies by offering step-by-step explanatio
15+ min read
Chapter 1: Rational Numbers
Chapter 2: Linear Equations in One Variable
Class 8 NCERT Solutions - Chapter 2 Linear Equations in One Variable - Exercise 2.1Question 1. Solve for x: x – 2 = 7 Solution: x – 2 = 7 x=7+2 (Adding two on both sides of equation) x=9 Question 2. Solve for y: y + 3 = 10 Solution: y + 3 = 10 y = 10 –3 (Subtracting 3 from both sides of equation) y = 7 Question 3. Solve for z: 6 = z + 2 Solution: 6 = z + 2 z + 2 = 6 (Rearranging t
3 min read
Class 8 NCERT Solutions - Chapter 2 Linear Equations in One Variable - Exercise 2.2Question 1. If you subtract 1/2 from a number and multiply the result by 1/2, you get 1/8 what is the number? Solution: Let the number be 'a'. According to the question, (a – 1/2) × 1/2 = 1/8 a/2 – 1/4 = 1/8 a/2 = 1/8 + 1/4 a/2 = 1/8 + 2/8 a/2 = (1 + 2)/8 a/2 = 3/8 a = (3/8) × 2 So, a = 3/4 Question
9 min read
Class 8 NCERT Solutions - Chapter 2 Linear Equations in One Variable - Exercise 2.3Question 1. Find the value of x : 3x = 2x + 18 Solution: 3x - 2x =18 (transposing 2x to LHS) X = 18 (solution) Verification — Put the value of x in the equation to verify our solution 3(18) = 2(18) + 18 54 = 36 + 18 54 = 54 LHS = RHS (so our value of x is correct) Question 2. Find the value of t : 5
5 min read
Class 8 NCERT Mathematics Solutions - Chapter 2 Linear Equations in One Variable - Exercise 2.4Chapter 2 of the Class 8 NCERT Mathematics textbook, "Linear Equations in One Variable," introduces students to solving linear equations, which are equations involving only one variable. Exercise 2.4 focuses on applying these concepts to solve a range of linear equations through various methods.In C
9 min read
Class 8 NCERT Solutions - Chapter 2 Linear Equations in One Variable - Exercise 2.5Content of this article has been updated in Class 8 NCERT Solutions – Chapter 2 Linear Equations in One Variable – Exercise 2.2 as per the new NCERT Syllabus Solve the following linear equations. Question 1. x/2 - 1/5 = x/3 + 1/4 Solution: (5x - 2)/10 = (4x + 3)/12 ...(Taking LCM on both the sides)
6 min read
Class 8 NCERT Solutions - Chapter 2 Linear Equations in One Variable - Exercise 2.6We use cross multiplication in this exercise a lot of times, so it is explained here before. Let, a/b = c/d Now if we multiply both sides by the denominators of left side and right side, we get, (a/b) X (b X d) = (c/d) X (b X d) => a X d = b X c This is called cross multiplication. Question.1 Sol
5 min read
Chapter 3: Understanding Quadrilaterals
Class 8 NCERT Solutions - Chapter 3 Understanding Quadrilaterals - Exercise 3.1In this section, we explore Chapter 3 of the Class 8 NCERT Mathematics textbook, which focuses on Understanding Quadrilaterals. This chapter introduces students to different types of quadrilaterals, their properties, and their classifications. Exercise 3.1 is designed to help students identify and a
5 min read
Class 8 NCERT Solutions - Chapter 3 Understanding Quadrilaterals - Exercise 3.2Question 1. Find x in the following figures. Solution: As we know , the sum of the measures of the external angles of any polygon is 360°. (a) 125° + 125° + x = 360° ⇒ 250° + x = 360° ⇒ x = 110° (a) 70° + 60° + x + 90° + 90° = 360° ⇒ 310° + x = 360° ⇒ x = 50° Question 2. Find the measure of each ext
3 min read
Class 8 NCERT Solutions- Chapter 3 Understanding Quadrilaterals - Exercise 3.3In this article, we will be going to solve the entire Exercise 3.3 of Chapter 3 of the NCERT textbook for Class 8. A quadrilateral is a polygon with four sides (edges), four vertices (corners), and four angles. It is one of the simplest types of polygons and can take various shapes depending on the
7 min read
Class 8 NCERT Solutions - Chapter 3 Understanding Quadrilaterals - Exercise 3.4In this section, we explore Chapter 3 of the Class 8 NCERT Mathematics textbook, titled "Understanding Quadrilaterals." This chapter introduces students to the different types of quadrilaterals, their properties, and the relationships between their angles and sides. Exercise 3.4 specifically focuses
4 min read
Chapter 4: Practical Geometry
Chapter 5: Data Handling
Chapter 6: Squares and Square Roots
Chapter 7: Cubes and Cube roots
Chapter 8: Comparing Quantities
Class 8 NCERT Solutions- Chapter 8 Comparing Quantities - Exercise 8.1In Chapter 8: Comparing Quantities students learn how to compare different values and express relationships between them in various forms such as ratios, percentages, and fractions. This chapter also introduces key concepts like profit and loss, simple interest, and discount helping students develop
6 min read
Class 8 NCERT Solutions - Chapter 8 Comparing Quantities - Exercise 8.2In Class 8, Chapter 8 of the NCERT Mathematics textbook focuses on the "Comparing Quantities" a crucial concept in understanding proportional relationships and percentage calculations. Exercise 8.2 of this chapter deals with the problems involving simple and compound interest crucial for developing
7 min read
Class 8 NCERT Solutions- Chapter 8 Comparing Quantities - Exercise 8.3In this section, we explore Chapter 8 of the Class 8 NCERT Mathematics textbook, which focuses on Comparing Quantities. This chapter introduces students to concepts like percentages, profit and loss, discounts, and simple interest. Exercise 8.3 specifically deals with problems related to calculating
14 min read
Chapter 9: Algebraic Expressions and Identities
Class 8 NCERT Solutions - Chapter 9 Algebraic Expressions and Identities - Exercise 9.1Question 1. Identify the terms, their coefficients for each of the following expressions.Need to be Known:Expression: An Expression is the addition of terms. Example: 7y + z is an expression made up of two terms 7y and z.Term: Terms itself is a product of factors. Example: 7y + z, here terms are 7y
7 min read
Class 8 NCERT Solutions - Chapter 9 Algebraic Expressions and Identities - Exercise 9.2Question 1. Find the product of the following pairs of monomials.Monomial: Expression containing only one term(i) 4, 7p Ans: (4) * (7p) = 28p (ii) -4p, 7pAns: (-4p) * (7p) = -28p2Explanation: When a negative number is multiplied to a positive number the product becomes negative.(iii) -4p, 7pqAns: (-
3 min read
Class 8 NCERT Solutions - Chapter 9 Algebraic Expressions and Identities - Exercise 9.3Chapter 9 of the Class 8 NCERT Mathematics textbook focuses on the Algebraic Expressions and Identities. Exercise 9.3 is designed to help students practice and understand the application of algebraic identities in simplifying and solving problems. This exercise covers key concepts related to algebra
6 min read
Class 8 NCERT Solutions- Chapter 9 Algebraic Expressions and Identities - Exercise 9.4Problem 1. Multiply the binomials.Solution:When we multiply two binomials, four multiplications must take place. These multiplications can be in any order, although we need to take care of that each of the first two terms is multiplied by each of the second terms. For example: (2x + 3)(3x – 1), if w
8 min read
Class 8 NCERT Solutions - Chapter 9 Algebraic Expressions and Identities - Exercise 9.5 | Set 1In this section, we dive into Chapter 9 of the Class 8 NCERT Mathematics textbook, which deals with Algebraic Expressions and Identities. This chapter introduces students to the concept of algebraic expressions, their components, and various identities that simplify expressions and solve equations.
9 min read
Class 8 NCERT Solutions - Chapter 9 Algebraic Expressions and Identities - Exercise 9.5 | Set 2Chapter 9 Algebraic Expressions and Identities - Exercise 9.5 | Set 1 Question 5. Show that:(i) (3x + 7)2 - 84x = (3x - 7)2Solution:L.H.S. = (3x + 7)2 - 84x= 9x2 + 42x + 49 - 84x= 9x2 - 42x + 49= (3x - 7)2= R.H.S.L.H.S. = R.H.S.(ii) (9p - 5q)2 + 180pq = (9p + 5q)2Solution:LHS = (9p - 5q)2 + 180pq= 8
5 min read