Binomial Heap

Last Updated : 02 Sep, 2024

The main application of Binary Heap is to implement a priority queue. Binomial Heap is an extension of Binary Heap that provides faster union or merge operation with other operations provided by Binary Heap.

A Binomial Heap is a collection of Binomial Trees
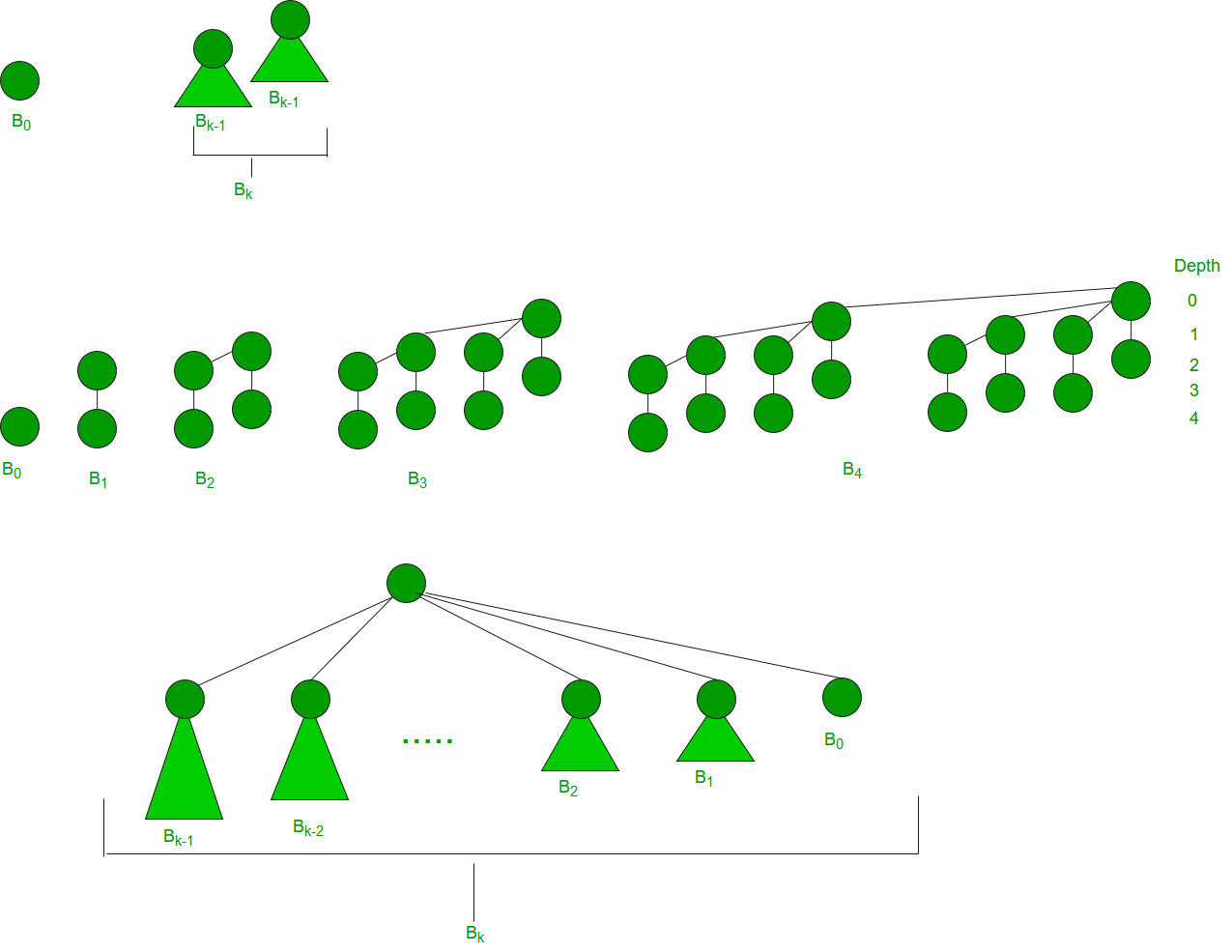
What is a Binomial Tree?

A Binomial Tree of order 0 has 1 node. A Binomial Tree of order k can be constructed by taking two binomial trees of order k-1 and making one the leftmost child of the other.

A Binomial Tree of order k the has following properties.

It has exactly 2^k nodes.
It has depth as k.
There are exactly kaiC_i nodes at depth i for i = 0, 1, . . . , k.
The root has degree k and children of the root are themselves Binomial Trees with order k-1, k-2,.. 0 from left to right.

k = 0 (Single Node)
 o
k = 1 (2 nodes) 
[We take two k = 0 order Binomial Trees, and
make one as a child of other]
  o
 /  
o     
k = 2 (4 nodes)
[We take two k = 1 order Binomial Trees, and
make one as a child of other]
     o
   /   \
  o     o
 /       
o        
k = 3 (8 nodes)
[We take two k = 2 order Binomial Trees, and
make one as a child of other]
        o   
     /  | \ 
    o   o  o
   / \  | 
  o   o o   
 /              
o

The following diagram is referred to form the 2nd Edition of the CLRS book.

BinomialTree

Binomial Heap:

A Binomial Heap is a set of Binomial Trees where each Binomial Tree follows the Min Heap property. And there can be at most one Binomial Tree of any degree.
Examples Binomial Heap:

12------------10--------------------20
             /  \                 /  | \
           15    50             70  50  40
           |                  / |    |     
           30               80  85  65 
                            |
                           100
A Binomial Heap with 13 nodes. It is a collection of 3 
Binomial Trees of orders 0, 2, and 3 from left to right. 
    10--------------------20
   /  \                 /  | \
 15    50             70  50  40
 |                  / |    |     
 30               80  85  65 
                  |
                 100

A Binomial Heap with 12 nodes. It is a collection of 2
Binomial Trees of orders 2 and 3 from left to right.

Programs to implement Binomial heap:

C++

// C++ program for the above approach #include <bits/stdc++.h> using namespace std;  // Class for each node in the Binomial Heap class Node { public:     int value;     Node* parent;     vector<Node*> children;     int degree;     bool marked;      Node(int val) {         value = val;         parent = nullptr;         children.clear();         degree = 0;         marked = false;     } };  // Class for the Binomial Heap data structure class BinomialHeap { public:     vector<Node*> trees;     Node* min_node;     int count;      // Constructor for the Binomial Heap     BinomialHeap() {         min_node = nullptr;         count = 0;         trees.clear();     }      // Check if the heap is empty     bool is_empty() {         return min_node == nullptr;     }      // Insert a new value into the heap     void insert(int value) {         Node* node = new Node(value);         BinomialHeap heap;         heap.trees.push_back(node);         merge(heap);     }      // Get the minimum value in the heap     int get_min() {         return min_node->value;     }      // Extract the minimum value from the heap     int extract_min() {         Node* minNode = min_node;         trees.erase(remove(trees.begin(), trees.end(), minNode), trees.end());         BinomialHeap heap;         heap.trees = minNode->children;         merge(heap);         _find_min();         count -= 1;         return minNode->value;     }      // Merge two binomial heaps     void merge(BinomialHeap& other_heap) {         trees.insert(trees.end(), other_heap.trees.begin(), other_heap.trees.end());         count += other_heap.count;         _find_min();     }      // Find the minimum value in the heap     void _find_min() {         min_node = nullptr;         for (Node* tree : trees) {             if (min_node == nullptr || tree->value < min_node->value) {                 min_node = tree;             }         }     }      // Decrease the key of a node     void decrease_key(Node* node, int new_value) {         if (new_value > node->value) {             throw invalid_argument("New value is greater than the current value");         }         node->value = new_value;         _bubble_up(node);     }      // Delete a specific node from the heap     void delete_node(Node* node) {         decrease_key(node, INT_MIN);         extract_min();     }      // Perform the bubbling up operation     void _bubble_up(Node* node) {         Node* parent = node->parent;         while (parent != nullptr && node->value < parent->value) {             swap(node->value, parent->value);             node = parent;             parent = node->parent;         }     }      // Link two trees together     void _link(Node* tree1, Node* tree2) {         if (tree1->value > tree2->value) {             swap(tree1, tree2);         }         tree2->parent = tree1;         tree1->children.push_back(tree2);         tree1->degree += 1;     }      // Consolidate the trees in the heap     void _consolidate() {         int max_degree = static_cast<int>(floor(log2(count))) + 1;         vector<Node*> degree_to_tree(max_degree + 1, nullptr);          while (!trees.empty()) {             Node* current = trees[0];             trees.erase(trees.begin());             int degree = current->degree;             while (degree_to_tree[degree] != nullptr) {                 Node* other = degree_to_tree[degree];                 degree_to_tree[degree] = nullptr;                 if (current->value < other->value) {                     _link(current, other);                 } else {                     _link(other, current);                     current = other;                 }                 degree++;             }             degree_to_tree[degree] = current;         }          min_node = nullptr;         trees.clear();         for (Node* tree : degree_to_tree) {             if (tree != nullptr) {                 trees.push_back(tree);                 if (min_node == nullptr || tree->value < min_node->value) {                     min_node = tree;                 }             }         }     }      // Get the size of the heap     int size() {         return count;     } };  // This code is contributed by Susobhan Akhuli

Java

// Java approach import java.util.*;  // Class for each node in the Binomial Heap class Node {     public int value;     public Node parent;     public List<Node> children;     public int degree;     public boolean marked;      public Node(int val) {         value = val;         parent = null;         children = new ArrayList<>();         degree = 0;         marked = false;     } }  // Class for the Binomial Heap data structure class BinomialHeap {     public List<Node> trees;     public Node min_node;     public int count;      // Constructor for the Binomial Heap     public BinomialHeap() {         min_node = null;         count = 0;         trees = new ArrayList<>();     }      // Check if the heap is empty     public boolean is_empty() {         return min_node == null;     }      // Insert a new value into the heap     public void insert(int value) {         Node node = new Node(value);         BinomialHeap heap = new BinomialHeap();         heap.trees.add(node);         merge(heap);     }      // Get the minimum value in the heap     public int get_min() {         return min_node.value;     }      // Extract the minimum value from the heap     public int extract_min() {         Node minNode = min_node;         trees.remove(minNode);         BinomialHeap heap = new BinomialHeap();         heap.trees = minNode.children;         merge(heap);         _find_min();         count -= 1;         return minNode.value;     }      // Merge two binomial heaps     public void merge(BinomialHeap other_heap) {         trees.addAll(other_heap.trees);         count += other_heap.count;         _find_min();     }      // Find the minimum value in the heap     public void _find_min() {         min_node = null;         for (Node tree : trees) {             if (min_node == null || tree.value < min_node.value) {                 min_node = tree;             }         }     }      // Decrease the key of a node     public void decrease_key(Node node, int new_value) {         if (new_value > node.value) {             throw new IllegalArgumentException("New value is greater than the current value");         }         node.value = new_value;         _bubble_up(node);     }      // Delete a specific node from the heap     public void delete_node(Node node) {         decrease_key(node, Integer.MIN_VALUE);         extract_min();     }      // Perform the bubbling up operation     public void _bubble_up(Node node) {         Node parent = node.parent;         while (parent != null && node.value < parent.value) {             int temp = node.value;             node.value = parent.value;             parent.value = temp;             node = parent;             parent = node.parent;         }     }      // Link two trees together     public void _link(Node tree1, Node tree2) {         if (tree1.value > tree2.value) {             Node temp = tree1;             tree1 = tree2;             tree2 = temp;         }         tree2.parent = tree1;         tree1.children.add(tree2);         tree1.degree += 1;     }      // Consolidate the trees in the heap     public void _consolidate() {         int max_degree = (int) Math.floor(Math.log(count) / Math.log(2)) + 1;         Node[] degree_to_tree = new Node[max_degree + 1];          while (!trees.isEmpty()) {             Node current = trees.get(0);             trees.remove(0);             int degree = current.degree;             while (degree_to_tree[degree] != null) {                 Node other = degree_to_tree[degree];                 degree_to_tree[degree] = null;                 if (current.value < other.value) {                     _link(current, other);                 } else {                     _link(other, current);                     current = other;                 }                 degree++;             }             degree_to_tree[degree] = current;         }          min_node = null;         trees.clear();         for (Node tree : degree_to_tree) {             if (tree != null) {                 trees.add(tree);                 if (min_node == null || tree.value < min_node.value) {                     min_node = tree;                 }             }         }     }      // Get the size of the heap     public int size() {         return count;     } }  // This code is contributed by Susobhan Akhuli

Python

import math   class Node:     def __init__(self, value):         self.value = value         self.parent = None         self.children = []         self.degree = 0         self.marked = False   class BinomialHeap:     def __init__(self):         self.trees = []         self.min_node = None         self.count = 0       def is_empty(self):         return self.min_node is None       def insert(self, value):         node = Node(value)         self.merge(BinomialHeap(node))       def get_min(self):         return self.min_node.value       def extract_min(self):         min_node = self.min_node         self.trees.remove(min_node)         self.merge(BinomialHeap(*min_node.children))         self._find_min()         self.count -= 1         return min_node.value       def merge(self, other_heap):         self.trees.extend(other_heap.trees)         self.count += other_heap.count         self._find_min()       def _find_min(self):         self.min_node = None         for tree in self.trees:             if self.min_node is None or tree.value < self.min_node.value:                 self.min_node = tree       def decrease_key(self, node, new_value):         if new_value > node.value:             raise ValueError("New value is greater than current value")         node.value = new_value         self._bubble_up(node)       def delete(self, node):         self.decrease_key(node, float('-inf'))         self.extract_min()       def _bubble_up(self, node):         parent = node.parent         while parent is not None and node.value < parent.value:             node.value, parent.value = parent.value, node.value             node, parent = parent, node       def _link(self, tree1, tree2):         if tree1.value > tree2.value:             tree1, tree2 = tree2, tree1         tree2.parent = tree1         tree1.children.append(tree2)         tree1.degree += 1       def _consolidate(self):         max_degree = int(math.log(self.count, 2))         degree_to_tree = [None] * (max_degree + 1)           while self.trees:             current = self.trees.pop(0)             degree = current.degree             while degree_to_tree[degree] is not None:                 other = degree_to_tree[degree]                 degree_to_tree[degree] = None                 if current.value < other.value:                     self._link(current, other)                 else:                     self._link(other, current)                 degree += 1             degree_to_tree[degree] = current           self.min_node = None         self.trees = [tree for tree in degree_to_tree if tree is not None]       def __len__(self):         return self.count

// C# program for the above approach using System; using System.Collections.Generic; using System.Linq;  // Class for each node in the Binomial Heap class Node {     public int Value;     public Node Parent;     public List<Node> Children;     public int Degree;     public bool Marked;      public Node(int val)     {         Value = val;         Parent = null;         Children = new List<Node>();         Degree = 0;         Marked = false;     } }  // Class for the Binomial Heap data structure class BinomialHeap {     public List<Node> Trees;     public Node MinNode;     public int Count;      // Constructor for the Binomial Heap     public BinomialHeap()     {         MinNode = null;         Count = 0;         Trees = new List<Node>();     }      // Check if the heap is empty     public bool IsEmpty() { return MinNode == null; }      // Insert a new value into the heap     public void Insert(int value)     {         Node node = new Node(value);         BinomialHeap heap = new BinomialHeap();         heap.Trees.Add(node);         Merge(heap);     }      // Get the minimum value in the heap     public int GetMin() { return MinNode.Value; }      // Extract the minimum value from the heap     public int ExtractMin()     {         Node minNode = MinNode;         Trees.Remove(minNode);         BinomialHeap heap = new BinomialHeap();         heap.Trees = minNode.Children;         Merge(heap);         FindMin();         Count -= 1;         return minNode.Value;     }      // Merge two binomial heaps     public void Merge(BinomialHeap otherHeap)     {         Trees.AddRange(otherHeap.Trees);         Count += otherHeap.Count;         FindMin();     }      // Find the minimum value in the heap     private void FindMin()     {         MinNode = null;         foreach(Node tree in Trees)         {             if (MinNode == null                 || tree.Value < MinNode.Value) {                 MinNode = tree;             }         }     }      // Decrease the key of a node     public void DecreaseKey(Node node, int newValue)     {         if (newValue > node.Value) {             throw new ArgumentException(                 "New value is greater than the current value");         }         node.Value = newValue;         BubbleUp(node);     }      // Delete a specific node from the heap     public void DeleteNode(Node node)     {         DecreaseKey(node, int.MinValue);         ExtractMin();     }      // Perform the bubbling up operation     private void BubbleUp(Node node)     {         Node parent = node.Parent;         while (parent != null                && node.Value < parent.Value) {             Swap(ref node.Value, ref parent.Value);             node = parent;             parent = node.Parent;         }     }      // Link two trees together     private void Link(Node tree1, Node tree2)     {         if (tree1.Value > tree2.Value) {             Swap(ref tree1, ref tree2);         }         tree2.Parent = tree1;         tree1.Children.Add(tree2);         tree1.Degree += 1;     }      // Consolidate the trees in the heap     private void Consolidate()     {         int maxDegree             = (int)Math.Floor(Math.Log2(Count)) + 1;         List<Node> degreeToTree = new List<Node>(             Enumerable.Repeat<Node>(null, maxDegree + 1));          while (Trees.Any()) {             Node current = Trees[0];             Trees.Remove(current);             int degree = current.Degree;             while (degreeToTree[degree] != null) {                 Node other = degreeToTree[degree];                 degreeToTree[degree] = null;                 if (current.Value < other.Value) {                     Link(current, other);                 }                 else {                     Link(other, current);                     current = other;                 }                 degree++;             }             degreeToTree[degree] = current;         }          MinNode = null;         Trees.Clear();         foreach(Node tree in degreeToTree)         {             if (tree != null) {                 Trees.Add(tree);                 if (MinNode == null                     || tree.Value < MinNode.Value) {                     MinNode = tree;                 }             }         }     }      // Get the size of the heap     public int Size() { return Count; }      // Helper method to swap two integers     private void Swap(ref int a, ref int b)     {         int temp = a;         a = b;         b = temp;     } }  // This code is contributed by Susobhan Akhuli

JavaScript

// Javascript program for the above approach  class Node {   constructor(value) {     this.value = value;     this.parent = null;     this.children = [];     this.degree = 0;     this.marked = false;   } }  class BinomialHeap {   constructor() {     this.trees = [];     this.min_node = null;     this.count = 0;   }    is_empty() {     return this.min_node === null;   }    insert(value) {     let node = new Node(value);     this.merge(new BinomialHeap(node));   }    get_min() {     return this.min_node.value;   }    extract_min() {     let min_node = this.min_node;     this.trees.splice(this.trees.indexOf(min_node), 1);     this.merge(new BinomialHeap(...min_node.children));     this._find_min();     this.count -= 1;     return min_node.value;   }    merge(other_heap) {     this.trees = [...this.trees, ...other_heap.trees];     this.count += other_heap.count;     this._find_min();   }    _find_min() {     this.min_node = null;     for (let tree of this.trees) {       if (this.min_node === null || tree.value < this.min_node.value) {         this.min_node = tree;       }     }   }    decrease_key(node, new_value) {     if (new_value > node.value) {       throw new Error("New value is greater than current value");     }     node.value = new_value;     this._bubble_up(node);   }    delete(node) {     this.decrease_key(node, -Infinity);     this.extract_min();   }    _bubble_up(node) {     let parent = node.parent;     while (parent !== null && node.value < parent.value) {       [node.value, parent.value] = [parent.value, node.value];       [node, parent] = [parent, node];     }   }    _link(tree1, tree2) {     if (tree1.value > tree2.value) {       [tree1, tree2] = [tree2, tree1];     }     tree2.parent = tree1;     tree1.children.push(tree2);     tree1.degree += 1;   }    _consolidate() {     let max_degree = Math.floor(Math.log2(this.count)) + 1;     let degree_to_tree = new Array(max_degree + 1).fill(null);      while (this.trees.length) {       let current = this.trees.shift();       let degree = current.degree;       while (degree_to_tree[degree] !== null) {         let other = degree_to_tree[degree];         degree_to_tree[degree] = null;         if (current.value < other.value) {           this._link(current, other);         } else {           this._link(other, current);         }         degree += 1;       }       degree_to_tree[degree] = current;     }      this.min_node = null;     this.trees = degree_to_tree.filter((tree) => tree !== null);   }    get length() {     return this.count;   } }  // This code is contributed by sdeadityasharma

Binary Representation of a number and Binomial Heaps
A Binomial Heap with n nodes has the number of Binomial Trees equal to the number of set bits in the binary representation of n. For example, let n be 13, there are 3 set bits in the binary representation of n (00001101), hence 3 Binomial Trees. We can also relate the degree of these Binomial Trees with positions of set bits. With this relation, we can conclude that there are O(Logn) Binomial Trees in a Binomial Heap with ‘n’ nodes.
Operations of Binomial Heap:
The main operation in Binomial Heap is a union(), all other operations mainly use this operation. The union() operation is to combine two Binomial Heaps into one. Let us first discuss other operations, we will discuss union later.

insert(H, k): Inserts a key ‘k’ to Binomial Heap ‘H’. This operation first creates a Binomial Heap with a single key ‘k’, then calls union on H and the new Binomial heap.
getting(H): A simple way to get in() is to traverse the list of the roots of Binomial Trees and return the minimum key. This implementation requires O(Logn) time. It can be optimized to O(1) by maintaining a pointer to the minimum key root.
extracting(H): This operation also uses a union(). We first call getMin() to find the minimum key Binomial Tree, then we remove the node and create a new Binomial Heap by connecting all subtrees of the removed minimum node. Finally, we call union() on H and the newly created Binomial Heap. This operation requires O(Logn) time.
delete(H): Like Binary Heap, the delete operation first reduces the key to minus infinite, then calls extracting().
decrease key(H): decrease key() is also similar to Binary Heap. We compare the decreased key with its parent and if the parent’s key is more, we swap keys and recur for the parent. We stop when we either reach a node whose parent has a smaller key or we hit the root node. The time complexity of the decrease key() is O(Logn).
Union operation in Binomial Heap:
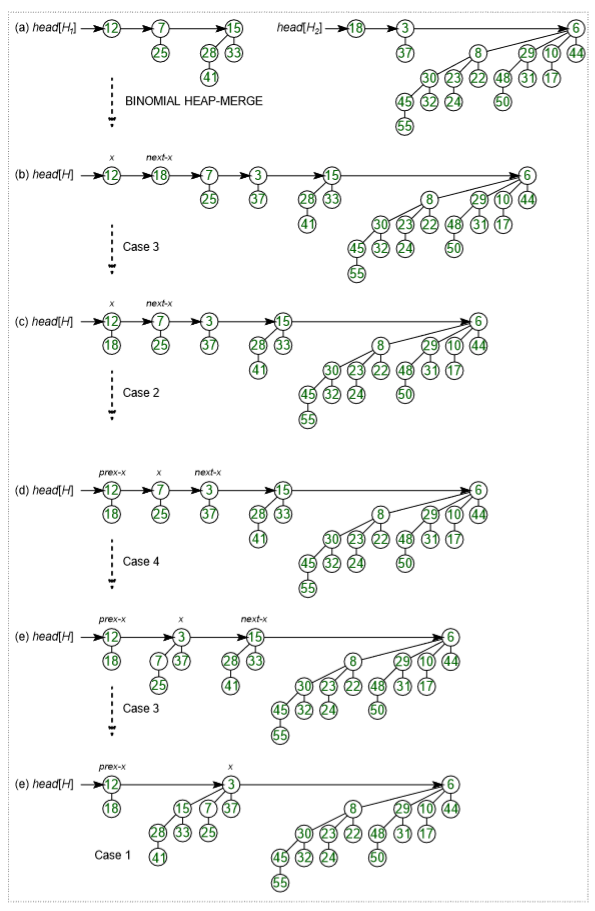
Given two Binomial Heaps H1 and H2, union(H1, H2) creates a single Binomial Heap.
The first step is to simply merge the two Heaps in non-decreasing order of degrees. In the following diagram, figure(b) shows the result after merging.
After the simple merge, we need to make sure that there is at most one Binomial Tree of any order. To do this, we need to combine Binomial Trees of the same order. We traverse the list of merged roots, we keep track of three-pointers, prev, x, and next-x. There can be the following 4 cases when we traverse the list of roots.
—–Case 1: Orders of x and next-x are not the same, we simply move ahead.
In the following 3 cases, orders of x and next-x are the same.
—–Case 2: If the order of next-next-x is also the same, move ahead.
—–Case 3: If the key of x is smaller than or equal to the key of next-x, then make next-x a child of x by linking it with x.
—–Case 4: If the key of x is greater, then make x the child of next.
The following diagram is taken from the 2nd Edition of the CLRS book.

BinomialHeapUnion

Time Complexity Analysis:

Operations	Binary Heap	Binomial Heap	Fibonacci Heap
Procedure	Worst-case	Worst-case	Amortized
Making Heap	Θ(1)	Θ(1)	Θ(1)
Inserting a node	Θ(log(n))	O(log(n))	Θ(1)
Finding Minimum key	Θ(1)	O(log(n))	O(1)
Extract-Minimum key	Θ(log(n))	Θ(log(n))	O(log(n))
Union or merging	Θ(n)	O(log(n))	Θ(1)
Decreasing a Key	Θ(log(n))	Θ(log(n))	Θ(1)
Deleting a node	Θ(log(n))	Θ(log(n))	O(log(n))

How to represent Binomial Heap?
A Binomial Heap is a set of Binomial Trees. A Binomial Tree must be represented in a way that allows sequential access to all siblings, starting from the leftmost sibling (We need this in and extracting() and delete()). The idea is to represent Binomial Trees as the leftmost child and right-sibling representation, i.e., every node stores two pointers, one to the leftmost child and the other to the right sibling.