Area of Rhombus: Formula, Derivation and Examples
Last Updated : 15 Jan, 2025
Rhombus is a parallelogram in which all four sides are equal and opposite pairs of lines are congruent. The opposite angles in a rhombus are equal. It is a special type of parallelogram in which all sides are equal to each other. The internal angle of the Rhombus is not mandatory to be a right angle.
The area of a Rhombus is the total space enclosed by its sides in a 2d Plane.
Using the formula based on the diagonals:
Area of RhombusWhere:
- p is the length of one diagonal.
- q is the length of the other diagonal
Note: Rhombus often gets confused with square but rhombus is very different from the square.
Read more: Why is a rhombus not a square?
Area of the rhombus can be found using various methods some of which are listed in the table below
| Area of Rhombus Formula |
|---|
| If Base and Height are given | A = b × h |
| If Diagonals are given | A = ½ × p × q |
| If Base and Interior angle is given | A = b2 × Sin(a) |
Where,
- p = length of first diagonal
- q = length of second diagonal
- b = length of side of rhombus
- h = height of rhombus
- a = measure of an interior angle
Below is the proof of area of Rhombus formula.
⇒ Let us consider a rhombus ABCD with O as the point of intersection of two diagonals AC and BD.
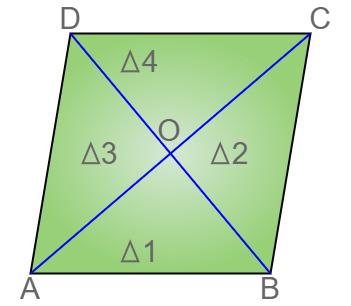Derivation of Area of RhombusThe area of rhombus will be
Area = 4 × area of △AOB
= 4 × (1/2) × AO × OB sq.units
= 4 × (1/2) × (1/2) d1 × (1/2) d2 sq. unit
= 4 × (1/8) d1 × d2
= 1/2 d1 × d2
Therefore, the area of a rhombus is A = 1/2 d1 × d2.
How to Find Area of Rhombus
The area of the rhombus can be calculated by three different methods: diagonal, using base and height, and using trigonometry.
These are the three important methods for finding area of Rhombus:
- Area of Rhombus when Diagonals are given
- Area of Rhombus using Base and Height
- Area of Rhombus using Trigonometric Ratios
Area of Rhombus with Diagonals
Area = (d1 × d2)/2 sq. units
Where,
d1 is the length of diagonal 1
d2 is the length of diagonal 2
Let's try to understand this formula with the help of an example.
Example 1: Find the area of a rhombus having diagonals 16 m and 18 m.
Solution:
Diagonal 1, d1 = 16 m
Diagonal 2, d2 = 18 m
Area of a rhombus, A = (d1 × d2) / 2
= (16 × 18) / 2
= 288 / 2
= 144 m2
Thus, the area of the rhombus is 144 m2
Area of Rhombus using Base and Height
Area of a Rhombus = b × h sq units
Where,
b is the length of any side of the rhombus
h is the height of the rhombus
Example 2: Find the area of a rhombus having base of 12 m and height is 16 m.
Solution:
Base, b = 12 m
Height, h = 16 m
Area, A = b × h
= 12 × 16 m2
A = 192 m2
Thus, the area of the rhombus is 192 m2
Area of Rhombus using Trigonometric Ratios
Area of a Rhombus = b2 × sin(A) sq. units
Where,
b is the length of any side of the rhombus
A is a measure of any interior angle
Example 3: Find the area of a rhombus if the length of its side is 12 m and one of its angles A is 60°
Solution:
Side = s = 12 m
Angle A = 60°
Area = s2 × sin (60°)
A = 144 × √3/2
A = 72√3 m2
Area of Rhombus Solved Examples
Example 1: Calculate the area of a rhombus (using base and height) if its base is 5cm and height is 3cm.
Solution:
Given, base (b) = 5cm
height of rhombus(h) = 3cm
Now, Area of the rhombus(A) = b × h
= 5 × 3
= 15cm2
Example 2: Calculate the area of a rhombus (using diagonal) having diagonals equal to 4cm and 3cm.
Solution:
Given, length of diagonal 1 (d1) = 4cm, Length of diagonal 2 (d2) = 3cm
Now,
Area of Rhombus (A) = 1/2 d1 × d2
= 4 x3/2 = 6cm2
Example 3: Calculate the area of the rhombus (using trigonometry) if its side is 8cm and one of its angles A is 30 degrees.
Solution:
Side of the rhombus (b) = 8cm, angle (a) = 30 degrees
Now,
Area of the rhombus(A) = b2 × sin(a)
= (8) × sin(30)
= 64 × 1/2 = 32 cm2
Example 4: Calculate the base of a rhombus if its area is 25cm2 and height is 10cm.
Solution:
Given,
Area = 25 cm2
height of rhombus(h) = 10 cm
Now,
Area of the rhombus(A) = b × h
25 = b × 10
= 2.5 cm
Area of Rhombus - Practice Problems
Question 1: Calculate the area of a rhombus with diagonals of 8 cm and 12 cm.
Question 2: The area of a rhombus is 54 cm². If one diagonal is 12 cm, find the length of the other diagonal.
Question 3: A rhombus has diagonals of 10 m and 16 m. What is its area in square meters?
Question 4: The diagonals of a rhombus are in the ratio 3:4, and its area is 150 cm². Find the lengths of the diagonals.
Question 5: The area of a rhombus is 40 m². If one diagonal is twice the length of the other, find the lengths of both diagonals.
Question 6: A square has a diagonal of 10√2 cm. What would be the area of a rhombus with diagonals equal to the sides of this square?
Question 7: The diagonals of a rhombus are 18 cm and 24 cm. Find the length of its side.
Question 8: A rhombus has an area of 96 cm² and one of its diagonals is 16 cm. What is the perimeter of the rhombus?
Answer Key
Answer 1: Area of a rhombus with diagonals 8 cm and 12 cm: 48 cm²
Answer 2: The other diagonal when the area is 54 cm² and one diagonal is 12 cm: 9 cm
Answer 3: Area of a rhombus with diagonals 10 m and 16 m: 80 m²
Answer 4: Diagonals of a rhombus with area 150 cm² and diagonals in the ratio 3:4: 15 cm and 20 cm
Answer 5: Diagonals of a rhombus with area 40 m² and one diagonal twice the other: 16 m and 8 m
Answer 6: Area of a rhombus with diagonals equal to the sides of a square with diagonal 10√2 cm: 50 cm²
Answer 7: Side length of a rhombus with diagonals 18 cm and 24 cm: 15 cm
Answer 8: Perimeter of a rhombus with area 96 cm² and one diagonal 16 cm: 40 cm
Related Articles:
Similar Reads
Mensuration in Maths Mensuration is a branch of mathematics that deals with measuring geometric figures, including their length, area, volume, and surface area. It provides formulas and techniques for calculating these attributes for 2D (plane) shapes and 3D (solid) objects.Types of Mensuration 2D Mensuration- Deals wit
4 min read
Introduction to Mensuration
Geometric Shapes in MathsGeometric shapes are mathematical figures that represent the forms of objects in the real world. These shapes have defined boundaries, angles, and surfaces, and are fundamental to understanding geometry. Geometric shapes can be categorized into two main types based on their dimensions:2D Shapes (Two
2 min read
Visualizing Solid ShapesVisualizing Solid Shapes: Any plane or any shape has two measurements length and width, which is why it is called a two-dimensional(2D) object. Circles, squares, triangles, rectangles, trapeziums, etc. are 2-D shapes. If an object has length, width, and breadth then it is a three-dimensional object(
8 min read
Volume of Combination of SolidsWhen two or more two solids are combined and the combination comes out useful, a shape that can be found in reality is called a combination of solids. When Solids are taught, the major focus is always on the point of their real-life use and applications, For example, a cylinder can be seen in Pipes
8 min read
Mensuration FormulasMensuration is the branch of geometry that deals with the measurement of area, length, or volume in 2D and 3D shapes. The 2D and 3D shapes are often called geometric shapes. In this article, we have curated all the mensuration formulas for various 2-D and 3-D shapes in detail.Mensuration FormulasTyp
10 min read
Perimeter
Perimeter of TriangleThe perimeter of a triangle is the total length of its three sides. A triangle is a polygon with three sides, three vertices, and three angles. It is the simplest closed polygon in geometry, as it is the first possible closed figure. Any polygon can be divided into triangles. For instance, a quadril
5 min read
How to find the perimeter of an equilateral triangle?The perimeter of an equilateral triangle is equal to 3 x a, where a is the length of any sideAn Equilateral triangle is a triangle in which all three sides are equal and the angles are also equal. The value of each angle of an equilateral triangle is 60 degrees therefore, it is also known as an equi
5 min read
Perimeter of an Isosceles TriangleA triangle can be considered as an isosceles triangle if and only if two sides of the triangle have the same length and two equal angles. The perimeter of an isosceles triangle comes under the parent topic mensuration which is a branch of geometry that deals with measurements of 2D/3D figures. Perim
5 min read
Perimeter of RectangleA rectangle is a two-dimensional plane quadrilateral, with opposite sides equal and all four angles equal. The perimeter of a rectangle can be defined as the sum of the length of all four sides in a rectangle.Perimeter of rectangle is the total length of the boundary or the sum of all its sides. In
7 min read
Perimeter of Square | Formula, Derivation, ExamplesA square is a four-sided polygon (quadrilateral) with the following properties.All sides are of equal length, and each angle is a right angle (90°). It is a type of rectangle where the length and width are the same.A square also has the property that its diagonals are equal in length and bisect each
4 min read
Perimeter of a ParallelogramA parallelogram is a type of quadrilateral with four equal sides with opposite sides equal. Its sides do not intersect each other. There are two diagonals of a parallelogram that intersect each other at the center. A diagonal divides the parallelogram into two equal parts or triangles. The following
7 min read
Perimeter of A RhombusPerimeter of a Rhombus is the sum of all the sides of the rhombus. In a rhombus, all the sides are equal so the perimeter of the rhombus is 4 times its side. The perimeter of Rhombus is calculated by the formula P = 4a where a is the side length of the perimeter. Now we can also find the perimeter o
6 min read
How to Find the Perimeter of a Trapezium?Suppose the sides of a Trapezium are a, b, c, and d then the Perimeter of the Trapezium is (a + b + c + d) units.Trapezium is a quadrilateral in which one pair of opposite sides are parallel. The perimeter of the trapezium is the sum of the boundaries of the trapezium. Suppose the sides of the trape
11 min read
Circumference of Circle - Definition, Perimeter Formula, and ExamplesThe circumference of a circle is the distance around its boundary, much like the perimeter of any other shape. It is a key concept in geometry, particularly when dealing with circles in real-world applications such as measuring the distance traveled by wheels or calculating the boundary of round obj
7 min read
Area
Area of a Triangle | Formula and ExamplesThe area of the triangle is a basic geometric concept that calculates the measure of the space enclosed by the three sides of the triangle. The formulas to find the area of a triangle include the base-height formula, Heron's formula, and trigonometric methods.The area of triangle is generally calcul
6 min read
Area of Equilateral TriangleThe area of an equilateral triangle is the amount of space enclosed within its three equal sides. For an equilateral triangle, where all three sides and all three internal angles are equal (each angle measuring 60 degrees), the area can be calculated using the formula \frac{\sqrt{3}}{4}\times a^{2}
6 min read
Right Angled Triangle | Properties and FormulaRight Angle Triangle is a type of triangle that has one angle measuring exactly 90 degrees or right angle (90°). It is also known as the right triangle. In a right triangle, the two shorter sides called the perpendicular and the base, meet at the right angle (90°), while the longest side, opposite t
6 min read
Heron's FormulaHeron's formula is a popular method for calculating the area of a triangle when the lengths of its three sides are known. It was introduced by Heron of Alexandria in his book "Metrica". This formula applies to all types of triangles, including right-angled, equilateral, and isosceles.According to th
9 min read
Area of SquareThe area of a Square is defined as the space enclosed by the boundary of the square. Measurement of the area is done in square units. The unit for measurement of the area is m2.Let's understand the Area of square with the following illustration:To calculate square's area we need to know the length o
7 min read
Area of RectangleArea of the Rectangle is the region covered inside the boundaries of the rectangle. The area of a rectangle is calculated using its dimensions length and breadth similar to the square in which the side is both the length and breadth.To find the area, you multiply the length of the rectangle by its w
9 min read
Area of Parallelogram | Definition, Formulas & ExamplesA parallelogram is a four-sided polygon (quadrilateral) where opposite sides are parallel and equal in length. In a parallelogram, the opposite angles are also equal, and the diagonals bisect each other (they cut each other into two equal parts).The area of a Parallelogram is the space or the region
8 min read
Area of Rhombus: Formula, Derivation and ExamplesRhombus is a parallelogram in which all four sides are equal and opposite pairs of lines are congruent. The opposite angles in a rhombus are equal. It is a special type of parallelogram in which all sides are equal to each other. The internal angle of the Rhombus is not mandatory to be a right angle
7 min read
Area of Trapezoid FormulaArea of a trapezoid is a concept in geometry that helps to calculate the space enclosed by the unique quadrilateral. Basically it is measured in square units. In this article we will discuss in detail how to find the area of a trapezoid.Before going to the formula of the area of the trapezoid let's
8 min read
Area of a Circle: Formula, Derivation, ExamplesThe area of a Circle is the measure of the two-dimensional space enclosed within its boundaries. It is mostly calculated by the size of the circle's radius which is the distance from the center of the circle to any point on its edge. The area of a circle is proportional to the radius of the circle.
10 min read
How to Calculate Area of Sector of Circle?Area of the sector is easily calculated by using various formulas of geometry. In this article, we have covered a definition of sector circles, types of sectors, and others in detail. Table of Content Sector DefinitionTypes of SectorsFormula for Area of a SectorExamples on Area of Sector of CircleFA
5 min read
Segment of a CircleSegment of a Circle is one of the important parts of the circle other than the sector. As we know, the circle is a 2-D shape in which points are equidistant from the point and the line connecting the two points lying on the circumference of the circle is called the chord of the circle. The area form
7 min read
Find the area of the shaded region formed by the intersection of four semicircles in a squareGiven the length of the side of a square a, the task is to find the area of the shaded region formed by the intersection of four semicircles in a square as shown in the image below: Examples: Input: a = 10 Output: 57Input: a = 19 Output: 205.77 Approach: Area of the shaded region will be: Area(semic
4 min read
3D Shape
Volume of a CubeVolume of a Cube is defined as the total number of cubic units occupied by the cube completely. A cube is a three-dimensional solid figure, having 6 square faces. Volume is nothing but the total space occupied by an object. An object with a larger volume would occupy more space. The volume of the cu
9 min read
Diagonal of a Cube FormulaDiagonal of a cube is the line segment joining the two non-adjacent vertices of a Cube. The diagonal of a cube formula helps us to calculate the length of diagonals in a cube. There are primarily two diagonals in a cube, namely face diagonals and body diagonals. In this article, we will learn the ty
8 min read
Volume of Cuboid | Formula and ExamplesVolume of a cuboid is calculated using the formula V = L × B × H, where V represents the volume in cubic units, L stands for length, B for breadth, and H for height. Here, the breadth and width of a cuboid are the same things. The volume signifies the amount of space occupied by the cuboid in three
8 min read
Volume of a SphereThe volume of a sphere helps us understand how much space a perfectly round object occupies, from tiny balls to large planets. Using the simple volume of sphere formula, you can easily calculate the space inside any sphere. Whether you're curious about the volume of a solid sphere in math or science
8 min read
Volume of HemisphereVolume of a shape is defined as how much capacity a shape has or we can say how much material was required to form that shape. A hemisphere, derived from the Greek words "hemi" (meaning half) and "sphere," is simply half of a sphere. If you imagine slicing a perfectly round sphere into two equal hal
6 min read
Volume of Cone- Formula, Derivation and ExamplesVolume of a cone can be defined as the space occupied by the cone. As we know, a cone is a three-dimensional geometric shape with a circular base and a single apex (vertex).Let's learn about Volume of Cone in detail, including its Formula, Examples, and the Frustum of Cone.Volume of ConeA cone's vol
9 min read
Volume of a Cylinder| Formula, Definition and ExamplesVolume of a cylinder is a fundamental concept in geometry and plays a crucial role in various real-life applications. It is a measure which signifies the amount of material the cylinder can carry. It is also defined as the space occupied by the Cylinder. The formula for the volume of a cylinder is π
11 min read
Volume of a Hollow CylinderA cylinder is a three-dimensional object that is formed when a rectangle is rotated along any of its sides. A hollow cylinder is one type of cylinder that is hollow from the inside. A hollow cylinder can be defined as a three-dimensional geometric object that is empty from the inside. A hollow cylin
8 min read
Convert Cubic Meter To Liter (m³ to L)Cubic meter (m³) and liter (L) are two of the most common metric units used to measure volume. Volume refers to the amount of three-dimensional space that an object or container occupies.The volume of a container is often referred to as its capacity. For instance, when we talk about the amount of fl
6 min read
Total Surface Area
Lateral or Curved Surface Area