Applications of Trigonometry in Real Life
Last Updated : 04 Dec, 2024
Trigonometry has a lot of real-life applications of trigonometry such as in astronomy to calculate the distance between planets and stars. Other than that, one application of trigonometry is the calculation of the height and distance of various objects in the real world.
Before understanding the application of Trigonometry, we need to understand some basic terms such as
Line of Sight
Consider a person looking at the top of the light tower as in the below figure:
.webp)
Line of Sight - TrigonometryIn this figure (given below), the line DE drawn from the eye of the boy to the top of the tower is called a Line of Sight.
Angle of Elevation
Consider a person looking at the top of the light tower as in the below figure:
.webp)
Angle of Elevation - TrigonometryThe angle between the line of sight and the horizontal level at the eye of the boy, ΔCDA or ∠D, is called the angle of elevation.
When we measure the angle of elevation, the observer should raise their head and look above the horizontal level.
Measure of Angle of ElevationHere if one wants to calculate the height of the tower without actually measuring it then what and how much information is required?
The following detail is necessary to find out the height of the tower without measuring it:
- Distance, AB or CD, between the tower and the point where the boy standing.
- The angle of elevation, ∠EDC, of the top of the tower.
- The height of the boy DA.
In ΔCDE, the known ∠D is the opposite of the side CE, and it is known that the side CD. So here is the trigonometry ratio, that can be used to apply all these three quantities. Determine tan D or cot D as their ratio involves CD and CE.
Angle of Depression
Now consider a situation as in given figure 4, a person is looking towards a ball from a balcony. Its line of sight is below the horizontal level. The angle between the line of sight and the horizontal level is called the angle of depression.
.webp)
Angle of Depression - TrigonometryThus, the angle of depression of the point on the object is the angle between the horizontal level and line of sight when the point is the below horizontal level.
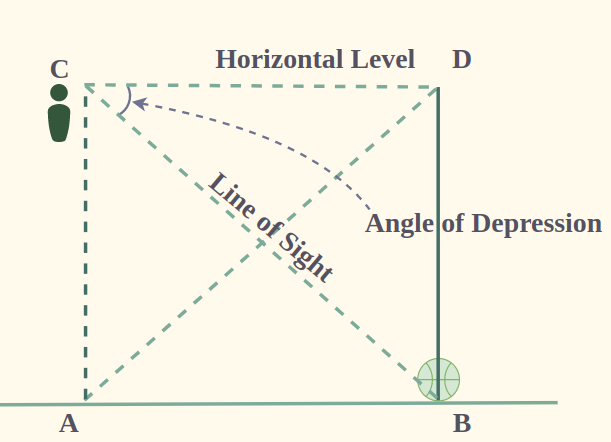Measure of Angle of DepressionIn the above figure, the person at point C, is looking towards the ball at B. CB is the line of sight and AC is the height of the balcony.
In ΔBCD, ∠BCD is the angle of depression of point B. Here is the height of the balcony AC = BD and the distance of the ball from the ground foot of the building AB = CD. According to the given data, the trigonometry ratio can be used as it can involve both known and unknown quantities.
Real-Life Applications of Trigonometry
There are various applications of trigonometry and some of the common applications of trigonometry are:
Trigonometry to Measure Height
The basic use or application of trigonometry is the measure of height. We use the concept of trigonometry to measure the height and distance between two objects by measuring the angles between these objects.
We can easily find the height of an object if we know the distance between any point and the foot of the building and the angle of elevation or the depression of that point from the building.
Trigonometry in Aviation
We use trigonometry in aviation for measuring the height and speed of any flying objects such as Airplanes and missiles.
The exact position of the airplane and other flying objects can be measured if we are given its height and the angle of elevation.
Trigonometry in Navigation
Trigonometry is widely used in the navigation of ships and others we can easily find the position of our ship in the ocean with the help of stars and the knowledge of trigonometry and angles.
Trigonometry in Astronomy
Trigonometry is widely used in astronomy to find the distances and positions of the stars and other heavenly bodies.
We can measure the angle of various heavenly bodies from the Earth by knowing the time taken by the light from that body to reach the Earth's surface and the speed of light we can find its position in space using trigonometry.
Other Uses of Trigonometry
The other uses of trigonometry are discussed below,
- It is used in criminology to study crime scenes such as determining path of bullets or crime scene reconstruction.
- It is used by marine biologists to study the depth of oceans using echo sounding or triangulation.
- It is used to study waves and their properties as waves in mathematics can be represented using sine or cosine functions.
Applications of Trigonometry - Solved Examples
Problem 1: A pole stands vertically on the plane. From a point on the plane, which is 12 m away from the foot of the pole, the angle of elevation of the top of the pole is 30° Find the height of the pole.
Solution:
First, draw a simple diagram of the given problem as below:
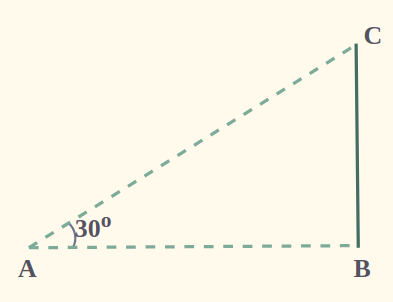
In this figure, BC represents the height of the electric pole and ∠CAB or ∠A represents the angle of the elevation of the top of the tower. In ΔABC, ∠CAB is the right angle and AB = 12 m. In ΔABC, CB is needed to be determined i.e. the height of the pole.
To solve the given problem, use trigonometry ratio tan A or cot A as they involve given sides in ratios.
Now, \tan A = \dfrac{CB}{AB}
\Rightarrow \tan 30^{\degree}=\dfrac{CB}{12}
\begin{aligned}\Rightarrow CB&=12\tan30^{\degree}\\ \Rightarrow CB &=4\sqrt{3}\text{ m}\end{aligned}
Hence, the height of the poll is 4√3.
Problem 2: The angle of elevation of the bird, who was sitting on a tree, from a point on the ground, which is 60 m away from the foot of the tree, is 60°. Find the height of the tree. (Take √3 = 1.73).
Solution:
First draw a simple diagram of the given problem as below:
In above figure, AB represents the distance between the ground point and foot of the tree, i.e. 60 m. BC is the height of the tree, let’s assume h.
In ΔABC, ∠ABC is the right angle, and the angle of the elevation is ∠B i.e. 60°.
Using trigonometry ratio tan A,
\tan A = \dfrac{BC}{AB}
\begin{aligned}\Rightarrow \tan 60{\degree}&=\dfrac{h}{60}\\ \Rightarrow h&=60\sqrt{3}\text{ m}\\\Rightarrow h &=103.8\text{ m}\end{aligned}
Hence, the height of the tree is 103.8 m.
Problem 3: A boy sees two clouds from a certain point. The angle of the elevation of the clouds are 30° and 45°. If the height of the clouds from the ground surface is the same and the distance between the clouds is 300 m then find out the height of the cloud.
Solution:
First, draw a simple diagram of the given problem as below.
In this figure, CE and BD represents the height of the clouds and ∠DAB and ∠EAC represents the angle of the elevation of the clouds at point A. In ΔABD, ∠DBA is the right angle, if the height of cloud BD is h then using trigonometry ratio tan A
\tan A=\dfrac{BD}{AB}
\Rightarrow \tan 45^{\degree}=\dfrac{h}{AB}
⇒ AB = h (Since, tan 45° = 1)
In ΔACE, ∠ACE is the right angle, if the height of cloud CE is h then using trigonometry ratio as:
\tan A = \dfrac{CE}{AC}
\Rightarrow \tan30^{\degree} = \dfrac{h}{AC}
\begin{aligned}\Rightarrow \dfrac{1}{\sqrt{3}}&=\dfrac{h}{AC}\\\Rightarrow AC&=h\sqrt{3}\end{aligned}
⇒ AC = h√3
From the above figure 4,
AC = AB + BC
Given: BC = 300.
Therefore, h√3 = h + 300
\begin{aligned}\Rightarrow h&=\frac{300}{\sqrt{3}-1}\\ \Rightarrow h&=410.96\text{ m}\end{aligned}
Hence, the height of the cloud is 410.96 m.
Problem 4: The angle of depression of a bike, standing in a park, from the top of a 45 m high building, is 30°. What is the distance of the bike from the base of the building (in m)?
Solution:
Below is a simple diagram of the given problem.
In above figure, AB represents the distance between the base of the building and the bike. AC is the height of the building, i.e. 45 m.
In ΔBCD, ∠BCD is the right angle and the angle of the depression is ∠C i.e. 30°. Using trigonometry ratio tan C in ΔBCD.
\tan C = \dfrac{BD}{CD}
Here AC = BD and AB = CD.
\begin{aligned}\tan 30{\degree}&=\dfrac{45\text{ m}}{AB}\\ \Rightarrow AB&=45\sqrt{3}\text{ m}\\\Rightarrow AB&=77.85\text{ m}\end{aligned}
Hence, the distance between the base of building and the bike is 77.85 m.
Problem 5: An electrician needs to repair an electric fault to solve the power supply issue in a village. The height of the electric pole, on which the fault exists, is 7 m. He wants to reach a point below 1.5 m from the top of the pole to repair the fault. What length of the ladder he should use to reach the required position if the ladder is inclined at 60° to the horizontal? Also, find how far the ladder he should place from the foot of the pole (Take √3 = 1.73).
Solution:
First, Draw a basic diagram of the given problem as below:
In this figure, BC is the ladder, AD is the total length of the pole, Point C is the where electrician wants to reach.
As given CD = 1.5 m and AD = 7 m.
Therefore,
AC = AD – CD
⇒ AC = 7 – 1.5 m
⇒ AC = 5.5 m
In ΔABC, ∠B is 60° and ∠A is right angle,
\sin B=\dfrac{AC}{BC}
\begin{aligned}\Rightarrow \sin 60{\degree}&=\dfrac{5.5}{BC}\\\Rightarrow BC&=5.5\times\dfrac{4}{\sqrt{3}}\\\Rightarrow BC&=12.71 \text{ m}\end{aligned}
And, in ΔABC,
\tan B=\dfrac{AC}{AB}
\begin{aligned}\tan 60{\degree}&=\dfrac{5.5}{AB}\\AB&=\dfrac{5.5}{\sqrt{3}}\\&=3.17 \text{m}\end{aligned}
Hence, the length of the ladder BC is 12.71 m and the distance between ladder and foot of the pole AB is 3.17 m.
Problem 6: The angle of elevation of a cloud from a point, which is somewhere on the surface of the water of a lake, is 30°. The angle of depression of the shadow of a cloud in the water of the lake from the same point is 60°. If the height of the cloud is 75 m then find the depth of the shadow. (Take √3 = 1.73).
Solution:
First, draw a basic diagram of the given problem as below:
In this figure, AB is the water surface of the lake. Points C and D represent the cloud and its shadow respectively. ∠ABC and ∠ABD are the right angles. BC is the height of the cloud, i.e. 75 m and BD is the depth of the shadow. ∠BAC and ∠BAD are the angle of elevation and the angle of the depression, i.e. 30° and 60°.
In ΔABC,
\tan A = \dfrac{BC}{AB}
\begin{aligned}\Rightarrow \tan 30{\degree}&=\dfrac{75}{AB}\\\Rightarrow AB&=75\sqrt{3}\text{ m}\\\Rightarrow AB&=129.75 \text{ m}\end{aligned}
Now in ΔABD,
\tan A = \dfrac{BC}{AB}
\begin{aligned}\Rightarrow \tan60{\degree}&=\dfrac{BD}{AB}\\\Rightarrow BD&=AB\sqrt{3}\text{ m}\\\Rightarrow BD&=224.46\text{ m}\end{aligned}
Hence, the depth of the shadow is 224.46 m.
Problem 7: Consider the following diagram:
If the √ACB is the right angle find the AB and CD (Take √3 = 1.73).
Solution:
In ΔACD, use the trigonometry ratio sin A,
\sin A = \dfrac{CD}{AD}
\begin{aligned}\Rightarrow & \sin 30{\degree}=\dfrac{CD}{5}\\ \Rightarrow &\dfrac{1}{2}=\dfrac{CD}{5}\\ \Rightarrow& CD=2.5 \text{ m}\end{aligned}
And,
\cos A = \dfrac{AC}{AD}
\begin{aligned}\Rightarrow \cos 30{\degree}&=\dfrac{AC}{5}\\ \Rightarrow \dfrac{\sqrt{3}}{2}&=\dfrac{AC}{5}\\ \Rightarrow AC&=4.33\text{ m}\end{aligned}
In ΔBCD, use the trigonometry ratio \tan B ,
\tan B = \dfrac{CD}{BC}
\begin{aligned}\tan45{\degree}&=\dfrac{CD}{BC}\\ \Rightarrow 1&=\dfrac{CD}{BC}\end{aligned}
⇒ BC = CD = 2.5 m
From the given figure:
AC = AB + BC
⇒ AB = 4.33 m – 2.5 m
⇒ AB =1.83 m
Hence, AB = 1.83 m and CD = 2.5 m.
Problem 8: A 1.5 m tall boy is looking toward two buildings. Both buildings have a height of 12 m. The elevation angle of the top of the buildings is 45° and 60°. Find the distance between the two buildings and the distance of the boy from the near building.
Solution:
A simple diagram of the given problem is drawn below
Figure 6In the above figure, CB and GH represent the two buildings, CG is the distance between the two buildings, CD and GD is the distance between the boy and foot of the buildings of EB and FH respectively.
In ΔCDE and ΔFDG,
EC = FG = EB – AD (Since, AD = CB = GH)
⇒ EC = FG = 12 m – 1.5 m
⇒ EC = FG = 10.5 m
In ΔCDE, ∠CDE is equal to 60\degreeand ∠DCE is the right angle.
\tan D=\dfrac{EC}{CD}
\begin{aligned}\Rightarrow \tan60{\degree}&=\dfrac{10.5}{CD}\\\Rightarrow CD&=\dfrac{10.5}{\sqrt{3}}\end{aligned}
\begin{aligned}\Rightarrow \tan60{\degree}&=\dfrac{10.5}{CD}\\\Rightarrow CD&=\dfrac{10.5}{\sqrt{3}}\\\Rightarrow CD&=6.07\text{ m}\end{aligned}
In ΔFDG, ∠FDG is 45{\degree} and ∠FGD is right angle.
\tan D = \dfrac{FG}{GD}
\begin{aligned}\Rightarrow \tan45{\degree}&=\dfrac{10.5}{GD}\\\Rightarrow GD&=10.5\text{ m}\end{aligned}
The distance between the buildings is:
CG = GD – CD
⇒ CG = 10.5 m – 6.07 m
⇒ CG = 4.43 m
Hence, the distance between the buildings CG is 4.43 m and the distance between the boy and the foot of the near building CD is 6.07 m.
People also ask:
Similar Reads
Chapter 1: Real Numbers
Chapter 2: Polynomials
Geometrical meaning of the Zeroes of a PolynomialAn algebraic identity is an equality that holds for any value of its variables. They are generally used in the factorization of polynomials or simplification of algebraic calculations. A polynomial is just a bunch of algebraic terms added together, for example, p(x) = 4x + 1 is a degree-1 polynomial
8 min read
Relationship between Zeroes and Coefficients of a PolynomialPolynomials are algebraic expressions with constants and variables that can be linear i.e. the highest power o the variable is one, quadratic and others. The zeros of the polynomials are the values of the variable (say x) that on substituting in the polynomial give the answer as zero. While the coef
9 min read
Division Algorithm for PolynomialsPolynomials are those algebraic expressions that contain variables, coefficients, and constants. For Instance, in the polynomial 8x2 + 3z - 7, in this polynomial, 8,3 are the coefficients, x and z are the variables, and 7 is the constant. Just as simple Mathematical operations are applied on numbers
5 min read
Division Algorithm Problems and SolutionsPolynomials are made up of algebraic expressions with different degrees. Degree-one polynomials are called linear polynomials, degree-two are called quadratic and degree-three are called cubic polynomials. Zeros of these polynomials are the points where these polynomials become zero. Sometimes it ha
6 min read
Chapter 3: Pair of Linear Equations in Two Variables
Pair of Linear Equations in Two VariablesLinear Equation in two variables are equations with only two variables and the exponent of the variable is 1. This system of equations can have a unique solution, no solution, or an infinite solution according to the given initial condition. Linear equations are used to describe a relationship betwe
11 min read
Number of Solutions to a System of Equations AlgebraicallyA statement that two mathematical expressions of one or more variables are identical is called an equation. Linear equations are those in which the powers of all the variables concerned are equal. A linear equation's degree is always one. A solution of the simultaneous pair of linear equations is a
7 min read
Graphical Methods of Solving Pair of Linear Equations in Two VariablesA system of linear equations is just a pair of two lines that may or may not intersect. The graph of a linear equation is a line. There are various methods that can be used to solve two linear equations, for example, Substitution Method, Elimination Method, etc. An easy-to-understand and beginner-fr
8 min read
Algebraic Methods of Solving Pair of Linear Equations in Two VariablesWhen solving a pair of linear equations in two variables, there are several algebraic methods you can use. Here’s a summary of the most common methods: Let's imagine a situation, Ankita went to a fair in her village. She wanted to go on rides like the Giant Wheel and play Hoopla (a game in which a r
9 min read
Equations Reducible to Linear FormEquations Reducible to Linear Form" refers to equations that can be transformed or rewritten into a linear equation. These equations typically involve variables raised to powers other than 1, such as squared terms, cubed terms, or higher. By applying suitable substitutions or transformations, these
9 min read
Chapter 4: Quadratic Equations
Quadratic EquationsA Quadratic equation is a second-degree polynomial equation that can be represented as ax2 + bx + c = 0. In this equation, x is an unknown variable, a, b, and c are constants, and a is not equal to 0. The solutions of a quadratic equation are known as its roots. These roots can be found using method
12 min read
Solving Quadratic EquationsA quadratic equation, typically in the form ax² + bx + c = 0, can be solved using different methods including factoring, completing the square, quadratic formula, and the graph method. While Solving Quadratic Equations we try to find a solution that represent the points where this the condition Q(x)
8 min read
Roots of Quadratic EquationThe roots of a quadratic equation are the values of x that satisfy the equation. The roots of a quadratic equation are also called zeros of a quadratic equation. A quadratic equation is generally in the form: ax2 + bx + c = 0Where:a, b, and c are constants (with a ≠0).x represents the variable.Root
13 min read
Chapter 5: Arithmetic Progressions
Arithmetic Progressions Class 10- NCERT NotesArithmetic Progressions (AP) are fundamental sequences in mathematics where each term after the first is obtained by adding a constant difference to the previous term. Understanding APs is crucial for solving problems related to sequences and series in Class 10 Mathematics. These notes cover the ess
7 min read
Arithmetic Progression - Common difference and Nth term | Class 10 MathsArithmetic Progression is a sequence of numbers where the difference between any two successive numbers is constant. For example 1, 3, 5, 7, 9....... is in a series which has a common difference (3 - 1) between two successive terms is equal to 2. If we take natural numbers as an example of series 1,
5 min read
Arithmetic Progression – Sum of First n Terms | Class 10 MathsArithmetic Progression is a sequence of numbers where the difference between any two successive numbers is constant. For example 1, 3, 5, 7, 9……. is in a series which has a common difference (3 – 1) between two successive terms is equal to 2. If we take natural numbers as an example of series 1, 2,
8 min read
Chapter 6: Triangles
Types of TrianglesA triangle is a polygon with three sides and three angles. It is one of the simplest and most fundamental shapes in geometry. A triangle has these key Properties:Sides: A triangle has three sides, which can have different lengths.Angles: A triangle has three interior angles, and the sum of these ang
5 min read
Angle Sum Property of a TriangleAngle Sum Property of a Triangle is the special property of a triangle that is used to find the value of an unknown angle in the triangle. It is the most widely used property of a triangle and according to this property, "Sum of All the Angles of a Triangle is equal to 180º." Angle Sum Property of a
8 min read
Construction of Similar TrianglesThe basic construction techniques allow the construction of perpendicular bisectors, angle bisectors, and so on. These basic techniques can be used for more complex constructions. These constructions are very essential for the designers who design buildings, roads, machines .. Etc. So, these techniq
8 min read
Criteria for Similarity of TrianglesThings are often referred similar when the physical structure or patterns they show have similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In
9 min read
Similar TrianglesSimilar Triangles are triangles with the same shape but can have variable sizes. Similar triangles have corresponding sides in proportion to each other and corresponding angles equal to each other. Similar triangles are different from congruent triangles. Two congruent figures are always similar, bu
15 min read
Pythagoras Theorem | Formula, Proof and ExamplesPythagoras Theorem explains the relationship between the three sides of a right-angled triangle and helps us find the length of a missing side if the other two sides are known. It is also known as the Pythagorean theorem. It states that in a right-angled triangle, the square of the hypotenuse is equ
9 min read
Basic Proportionality Theorem (BPT) Class 10 | Proof and ExamplesBasic Proportionality Theorem: Thales theorem is one of the most fundamental theorems in geometry that relates the parts of the length of sides of triangles. The other name of the Thales theorem is the Basic Proportionality Theorem or BPT. BPT states that if a line is parallel to a side of a triangl
8 min read
Criteria for Similarity of TrianglesThings are often referred similar when the physical structure or patterns they show have similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In
9 min read
Chapter 7: Coordinate Geometry
Coordinate GeometryCoordinate geometry is a branch of mathematics that combines algebra and geometry using a coordinate plane. It helps us represent points, lines, and shapes with numbers and equations, making it easier to analyze their positions, distances, and relationships. From plotting points to finding the short
3 min read
Distance formula - Coordinate Geometry | Class 10 MathsThe distance formula is one of the important concepts in coordinate geometry which is used widely. By using the distance formula we can find the shortest distance i.e drawing a straight line between points. There are two ways to find the distance between points:Pythagorean theoremDistance formulaTab
9 min read
Section FormulaSection Formula is a useful tool in coordinate geometry, which helps us find the coordinate of any point on a line which is dividing the line into some known ratio. Suppose a point divides a line segment into two parts which may be equal or not, with the help of the section formula we can find the c
14 min read
Mid Point Formula in Coordinate GeometryMid point formula in coordinate geometry provides a way to find the mid point of a line segment when the coordinates of the starting and ending points ( i.e. (x1, y1) and (x2, y2) )of the line segment is known. The mid point divides the line in two equal halves i.e the ratio of the sections of the l
6 min read
Area of a Triangle in Coordinate GeometryThere are various methods to find the area of the triangle according to the parameters given, like the base and height of the triangle, coordinates of vertices, length of sides, etc. In this article, we will discuss the method of finding area of any triangle when its coordinates are given.Area of Tr
6 min read
Chapter 8: Introduction to Trigonometry
Trigonometric RatiosThere are three sides of a triangle Hypotenuse, Adjacent, and Opposite. The ratios between these sides based on the angle between them is called Trigonometric Ratio. The six trigonometric ratios are: sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec).As give
4 min read
Trigonometric Ratios of Some Specific AnglesTrigonometry is all about triangles or to be more precise the relationship between the angles and sides of a triangle (right-angled triangle). In this article, we will be discussing the ratio of sides of a right-angled triangle concerning its acute angle called trigonometric ratios of the angle and
6 min read
Reciprocal of Trigonometric RatiosTrigonometry is all about triangles or to be more precise about the relation between the angles and sides of a right-angled triangle. In this article, we will be discussing about the ratio of sides of a right-angled triangle with respect to its acute angle called trigonometric ratios of the angle an
5 min read
Trigonometric IdentitiesTrigonometric identities play an important role in simplifying expressions and solving equations involving trigonometric functions. These identities, which include relationships between angles and sides of triangles, are widely used in fields like geometry, engineering, and physics. Some important t
10 min read
Applications of Trigonometry in Real LifeTrigonometry has a lot of real-life applications of trigonometry such as in astronomy to calculate the distance between planets and stars. Other than that, one application of trigonometry is the calculation of the height and distance of various objects in the real world.Before understanding the appl
12 min read
Chapter 9: Some Applications of Trigonometry
Chapter 10: Circles