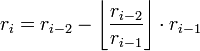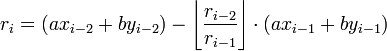Power Series Evaluation

Power series evaluation in O(lg(n)):[n is the number of terms]

We'll try to evaluate the following power series in logarithmic time w.r.t. the number of terms n.


Well well... I may be asked, "dude, why do you want to do this in O(lg(n)) when there's already we have a O(1) solution for your problem?". Answer is simple, "I'm trying it from a programming perspective and the O(1) can get sometimes impossible when n keeps going up i.e. like 10¹⁰⁰⁰ and you are asked to return the answer w.r.t. some %m [modulus m] (meaning the final result will not reach m). This method will be suitable for this case only. Because, calculating {(x^n-1-1)/(x-1)}%m is not a very easy task and sometimes, it is not directly possible.

This series can be evaluated by binary splitting and recursively solving those building up the answer.
Let n = 6
We have, 1 + x + x² + x³ + x⁴ + x⁵
⇒ (1 + x + x²) + x³(1 + x + x²)
⇒ (1 + x + x²)(1 + x³)

So, when n is even, f(x, n) = (1 + x^n/2)f(x, n/2)

Now, what if n is odd, Let n = 7
We have, 1 + x + x² + x³ + x⁴ + x⁵ + x⁶
⇒ (1 + x + x²) + x³(1 + x + x²) + x⁶
⇒ (1 + x + x²)(1 + x³) + x⁶

So, when n is odd, f(x, n) = (1 + x^n/2)f(x, n/2) + x^n-1

So, by combining the above 2 equations, we get the final solution:
f(x, n) = (1 + x^n/2)f(x, n/2) + (n%2)x^n-1

By some clever observation, the need for -1 and %2 operation on n can be eliminated. So, the only thing we need to do is the /2 operation on n, which is easy even when n is a big integer.

Here is a python module that shows only the recursive part, no trick applied.

import math

def evaluate(x, n):
    if(n==0):
        return 0
    if(n==1):
        return 1
    ret = 0
    if(n%2==1):
        ret = ret + int(math.pow(x, n-1))
    n = n/2
    return ret + evaluate(x, n)*(1 + int(math.pow(x, n)))

If this is to be done with C/C++, some biginteger division algorithm should be implemented.

Easy, eh? Check different types of series here

Extended Euclidean Algorithm

Extended Euclidean Algorithm is an extension of standard Euclidean Algorithm for finding the GCD of two integers a and b. It also calculates the values of two more integers x and y such that: ax + by = gcd(a,b); where typically either x or y is negative. This algorithm is generally used to find multiplicative inverse in a finite field, because, if ax + by = gcd(a,b) = 1, i.e. a and be are co-primes, then x is the modular multiplicative inverse of a modulo b, and similarly, y is the modular multiplicative inverse of b modulo a.

This method computes expressions of the form r_i = ax_i + by_i for the remainder in each step i of the Euclidean algorithm. Each modulus can be written in terms of the previous two remainders and their whole quotient as follows:

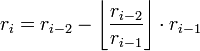
By substitution, this gives:

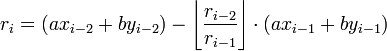
The first two values are the initial arguments to the algorithm:

r₁ = a = a(1) + b(0)

r₂ = b = a(0) + b(1)

The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.

Example: Compute the GCD of 120 and 23. Or, more formally, compute: x, y, g for 120x + 23y = g; where x, y are two integers and g is the gcd of 120 and 23...

The computation proceeds as follows:

Initial values:
Step 1: Reminder = 120;
Combine terms: 120 = 120 x 1 + 23 x 0

Step 2: Reminder = 23;
Combine terms: 23 = 120 x 0 + 23 x 1

Iterative steps:
Step 3: Quotient = 120 / 23 = 5; Reminder = 120 % 23 = 5;
5 = 120 - 23 x 5
=> 5 = (120 x 1 + 23 x 0) - (120 x 0 + 23 x 1) x 5 ;[from Step 1 and 2]
=> 5 = 120 x 1 + 23 x -5

Step 4: Quotient = 23 / 5 = 4; Reminder = 23 % 5 = 3;
3 = 23 - 5 x 4
=> 3 = (120 x 0 + 23 x 1) - (120 x 1 + 23 x -5) x 4 ;[from Step 2 and 3]
=> 3 = 120 x -4 + 23 x 21

Step 5: Quotient = 5 / 3 = 1; Reminder = 5 % 3 = 2;
2 = 5 - 3 x 1
=> 2 = (120 x 1 + 23 x -5) - (120 x -4 + 23 x 21) x 1 ;[from Step 3 and 4]
=> 2 = 120 x 5 + 23 x -26

Step 6: Quotient = 3 / 2 = 1; Reminder = 3 % 2 = 1;
1 = 3 - 2 x 1
=> 1 = (120 x -4 + 23 x 21) - (120 x 5 + 23 x -26) x 1 ;[from Step 4 and 5]
=> 1 = 120 x -9 + 23 x 47
End of Algorithm.

The last line reads 1 = −9×120 + 47×23, which is the required solution: x = −9 and y = 47, and obviously g = gcd(120,23) = 1

This also means that −9 is the multiplicative inverse of 120 modulo 23, and that 47 is the multiplicative inverse of 23 modulo 120.

−9 × 120 ≡ 1 mod 23 and also 47 × 23 ≡ 1 mod 120.

Algorithm:
By routine algebra of expanding and grouping like terms (refer to the previous example), the following algorithm for iterative method is obtained:

1. Apply Euclidean algorithm, and let q_n(n starts from 1) be a finite list of quotients in the division.
2. Initialize x₀, x₁ as 1, 0, and y₀, y₁ as 0,1 respectively.
3. Then for each i so long as q_i is defined,

• Compute x_i+1= x_i-1- q_ix_i
• Compute y_i+1= y_i-1- q_iy_i
• Repeat the above after incrementing i by 1.

The answers are the second-to-last of x_n and y_n.

Sample Program:
Here is a sample program written in C++ which implements the Extended Euclidean Algorithm:

#include <stdio.h>
/*
Takes a, b as input.
Returns gcd(a, b).
Updates x, y via pointer reference.
*/
int Extended_Euclid(int A, int B, int *X, int *Y)
{
    int x, y, u, v, m, n, a, b, q, r;
 
    /* B = A(0) + B(1) */
    x = 0; y = 1;
 
    /* A = A(1) + B(0) */
    u = 1; v = 0;
 
    for (a = A, b = B; 0 != a; b = a, a = r, x = u, y = v, u = m, v = n)
    {
        /* b = aq + r and 0 <= r < a */
        q = b / a;
        r = b % a;
 
        /* r = Ax + By - aq = Ax + By - (Au + Bv)q = A(x - uq) + B(y - vq) */
        m = x - (u * q);
        n = y - (v * q); 
    }   
 
    /* Ax + By = gcd(A, B) */
    *X = x; *Y = y;
 
    return b;
}

int main()
{
    int a, b, x, y, g;
    scanf("%d %d", &a, &b);
    g = Extended_Euclid(a, b, &x, &y);
    printf("X = %d; Y = %d; G = %d\n", x, y, g);
    return 0;
}

Python implementation:

def Extended_Euclid(a, b):
    x, last_x = 0, 1
    y, last_y = 1, 0
 
    while b:
        quotient = a / b
        a, b = b, a % b
        x, last_x = last_x - quotient*x, x
        y, last_y = last_y - quotient*y, y
 
    return (last_x, last_y, a)

For complete reading, click here. It is also useful to have a look at the Chinese Remainder Theorem.

Hope this will help...

Negative Base Number System

Negative-base systems can accommodate all the same numbers as standard place-value systems; but both positive and negative numbers are represented without the use of a minus sign (or, in computer representation, a sign bit); this advantage is countered by an increased complexity of arithmetic operations. The need to store the "information" normally contained by a negative sign often results in a negative-base number being one digit longer than its positive-base equivalent.


The common names for negative-base positional numeral systems are formed by prefixing nega- to the name of the corresponding positive-base system; for example, negadecimal (base -10) corresponds to decimal (base 10), negaternary (base -3) to ternary (base 3), and negabinary (base -2) to binary (base 2).

Denoting the base as − r, every integer a can be written uniquely as:

where each digit d_k is an integer from 0 to r − 1 and the leading digit d_n is > 0 (unless n=0). The base − r expansion of a is then given by the string d_nd_n-1.....d₁d₀.


Calculation:

The base − r expansion of a number can be found by repeated division by − r, recording the non-negative remainders of 0,1,2,.........,r-1; and concatenating those remainders, starting with the last. Note that if a / b = c, remainder d, then bc + d = a. For example, 146 in negaternary:

146 / -3 = -48; reminder = 2
-48 / -3 =  16; reminder = 0
 16 / -3 =  -5; reminder = 1
 -5 / -3 =   2; reminder = 1
  2 / -3 =   0; reminder = 2

Therefore, the negaternary expansion of 146 is 21102.

Note that in most programming languages, the result (in integer arithmetic) of dividing a negative number by a negative number is rounded towards 0, usually leaving a negative remainder; to get the correct result in such case, computer implementations of the above algorithm should add 1 and r to the quotient and remainder respectively.

The numbers -15 to 15 with their expansions in a number of positive and corresponding negative bases are:

Decimal	Negadecimal	Binary	Negabinary	Ternary	Negaternary
-15	25	-1111	110001	-120	1220
-14	26	-1110	110110	-112	1221
-13	27	-1101	110111	-111	1222
-12	28	-1100	110100	-110	1210
-11	29	-1011	110101	-102	1211
-10	10	-1010	1010	-101	1212
-9	11	-1001	1011	-100	1200
-8	12	-1000	1000	-22	1201
-7	13	-111	1001	-21	1202
-6	14	-110	1110	-20	20
-5	15	-101	1111	-12	21
-4	16	-100	1100	-11	22
-3	17	-11	1101	-10	10
-2	18	-10	10	-2	11
-1	19	-1	11	-1	12
0	0	0	0	0	0
1	1	1	1	1	1
2	2	10	110	2	2
3	3	11	111	10	120
4	4	100	100	11	121
5	5	101	101	12	122
6	6	110	11010	20	110
7	7	111	11011	21	111
8	8	1000	11000	22	112
9	9	1001	11001	100	100
10	190	1010	11110	101	101
11	191	1011	11111	102	102
12	192	1100	11100	110	220
13	193	1101	11101	111	221
14	194	1110	10010	112	222
15	195	1111	10011	120	210

Note that the base − r expansions of negative integers have an even number of digits, while the base − r expansions of the non-negative integers have an odd number of digits.

Program for calculating Negabinary

In python:

def negabinary(i):
    digits = []  
    while i != 0:
        i, remainder = divmod(i, -2)
        if remainder < 0:
            i, remainder = i + 1, remainder + 2
        digits.insert(0, str(remainder))
    return ''.join(digits)

In C++:

string negabinary(int i)
{
    int reminder;
    string digits;
    while(i != 0)
    {
        reminder = i % -2;
        i /= -2;
        if(reminder < 0)
        {
            i++;
            reminder += 2;
        }
        digits.push_back(reminder+'0');
    }
    reverse(digits.begin(),digits.end());
    return digits;
}

The same procedure it to be followed for calculating other negative number system.

Source: Wikipedia