Introduction to Recursion

Last Updated : 24 Apr, 2025

The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called a recursive function.

A recursive algorithm takes one step toward solution and then recursively call itself to further move. The algorithm stops once we reach the solution.
Since called function may further call itself, this process might continue forever. So it is essential to provide a base case to terminate this recursion process.

Need of Recursion

Recursion helps in logic building. Recursive thinking helps in solving complex problems by breaking them into smaller subproblems.
Recursive solutions work as a a basis for Dynamic Programming and Divide and Conquer algorithms.
Certain problems can be solved quite easily using recursion like Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc.

Steps to Implement Recursion

Step1 – Define a base case: Identify the simplest (or base) case for which the solution is known or trivial. This is the stopping condition for the recursion, as it prevents the function from infinitely calling itself.

Step2 – Define a recursive case: Define the problem in terms of smaller subproblems. Break the problem down into smaller versions of itself, and call the function recursively to solve each subproblem.

Step3 – Ensure the recursion terminates: Make sure that the recursive function eventually reaches the base case, and does not enter an infinite loop.

Step4 – Combine the solutions: Combine the solutions of the subproblems to solve the original problem.

Example 1 : Sum of Natural Numbers

Let us consider a problem to find the sum of natural numbers, there are several ways of doing that but the simplest approach is simply to add the numbers starting from 0 to n.

Comparison of Recursive and Iterative Approaches

Approach	Complexity	Memory Usage
Iterative Approach	O(n)	O(1)
Recursive Approach	O(n)	O(n)

C++

#include <iostream> using namespace std;  // Recursive function to find the sum of  // numbers from 0 to n int findSum(int n) {     // Base case      if (n == 1)          return 1;         // Recursive case      return n + findSum(n - 1); }  int main() {     int n = 5;     cout << findSum(n);     return 0; }

#include <stdio.h>  // Recursive function to find the sum of  // numbers from 0 to n int findSum(int n) {     // Base case      if (n == 1)          return 1;         // Recursive case      return n + findSum(n - 1); }  int main() {     int n = 5;     printf("%d", findSum(n));     return 0; }

Java

public class Main {     // Recursive function to find the sum of      // numbers from 0 to n     static int findSum(int n) {         // Base case          if (n == 1)              return 1;                   // Recursive case          return n + findSum(n - 1);     }      public static void main(String[] args) {         int n = 5;         System.out.println(findSum(n));     } }

Python

def findSum(n):     # Base case      if n == 1:         return 1          # Recursive case      return n + findSum(n - 1)  n = 5 print(findSum(n))

using System;  class Program {     // Recursive function to find the sum of      // numbers from 0 to n     static int FindSum(int n) {         // Base case          if (n == 1)              return 1;                  // Recursive case          return n + FindSum(n - 1);     }      static void Main() {         int n = 5;         Console.WriteLine(FindSum(n));     } }

JavaScript

// Recursive function to find the sum of  // numbers from 0 to n function findSum(n) {     // Base case      if (n === 1)          return 1;          // Recursive case      return n + findSum(n - 1); }  let n = 5; console.log(findSum(n));

Output

What is the base condition in recursion?
A recursive program stops at a base condition. There can be more than one base conditions in a recursion. In the above program, the base condition is when n = 1.

How a particular problem is solved using recursion?
The idea is to represent a problem in terms of one or more smaller problems, and add one or more base conditions that stop the recursion.

Example 2 : Factorial of a Number

The factorial of a number n (where n >= 0) is the product of all positive integers from 1 to n. To compute the factorial recursively, we calculate the factorial of n by using the factorial of (n-1). The base case for the recursive function is when n = 0, in which case we return 1.

C++

#include <iostream> using namespace std;  int fact(int n) {     // BASE CONDITION     if (n == 0)         return 1;        return n * fact(n - 1); }  int main() {     cout << "Factorial of 5 : " << fact(5);     return 0; }

#include <stdio.h>  int fact(int n) {        // BASE CONDITION     if (n == 0)         return 1;        return n * fact(n - 1); }  int main() {     printf("Factorial of 5 : %d\n", fact(5));     return 0; }

Java

public class GfG {     public static int fact(int n) {                // BASE CONDITION         if (n == 0)             return 1;                return n * fact(n - 1);     }      public static void main(String[] args) {         System.out.println("Factorial of 5 : " + fact(5));     } }

Python

def fact(n):        # BASE CONDITION     if n == 0:         return 1     return n * fact(n - 1)  print("Factorial of 5 : ", fact(5))

using System;  class Program {     static int Fact(int n) {                // BASE CONDITION         if (n == 0)             return 1;                  return n * Fact(n - 1);     }      static void Main() {         Console.WriteLine("Factorial of 5 : " + Fact(5));     } }

JavaScript

function fact(n) {      // BASE CONDITION     if (n === 0)         return 1;          return n * fact(n - 1); }  console.log("Factorial of 5 : " + fact(5));

PHP

<?php function fact($n) {        // BASE CONDITION     if ($n == 0)         return 1;        return $n * fact($n - 1); }  echo "Factorial of 5 : " . fact(5); ?>

Output

Factorial of 5 : 120

Illustration of the above code:

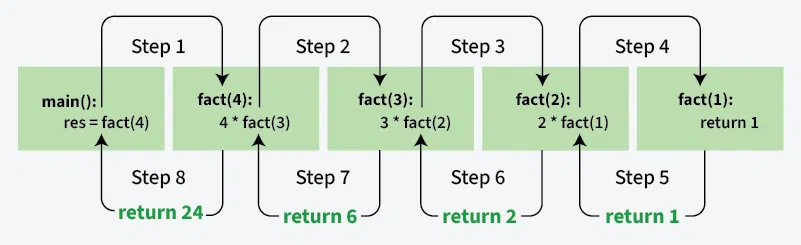
When does Stack Overflow error occur in recursion?

If the base case is not reached or not defined, then the stack overflow problem may arise. Let us take an example to understand this.

int fact(int n)
{
// wrong base case (it may cause stack overflow).
if (n == 100)
return 1;
else
return n*fact(n-1);
}

In this example, if fact(10) is called, the function will recursively call fact(9), then fact(8), fact(7), and so on. However, the base case checks if n == 100. Since n will never reach 100 during these recursive calls, the base case is never triggered. As a result, the recursion continues indefinitely.

This continuous recursion consumes memory on the function call stack. If the system’s memory is exhausted due to these unending function calls, a stack overflow error occurs.

To prevent this, it’s essential to define a proper base case, such as if (n == 0) to ensure that the recursion terminates and the function doesn’t run out of memory.

What is the difference between direct and indirect recursion?

A function is called direct recursive if it calls itself directly during its execution. In other words, the function makes a recursive call to itself within its own body.

An indirect recursive function is one that calls another function, and that other function, in turn, calls the original function either directly or through other functions. This creates a chain of recursive calls involving multiple functions, as opposed to direct recursion, where a function calls itself.

// An example of direct recursion
void directRecFun()
{
// Some code….

directRecFun();

// Some code…
}

// An example of indirect recursion
void indirectRecFun1()
{
// Some code…

indirectRecFun2();

// Some code…
}
void indirectRecFun2()
{
// Some code…

indirectRecFun1();

// Some code…
}

What is the difference between tail and non-tail recursion?

A recursive function is tail recursive when a recursive call is the last thing executed by the function.

Please refer tail recursion for details.

How memory is allocated to different function calls in recursion?

Recursion uses more memory to store data of every recursive call in an internal function call stack.

Whenever we call a function, its record is added to the stack and remains there until the call is finished.
The internal systems use a stack because function calling follows LIFO structure, the last called function finishes first.

When any function is called from main(), the memory is allocated to it on the stack. A recursive function calls itself, the memory for a called function is allocated on top of memory allocated to the calling function and a different copy of local variables is created for each function call. When the base case is reached, the function returns its value to the function by whom it is called and memory is de-allocated and the process continues.
Let us take the example of how recursion works by taking a simple function.

C++

// A C++ program to demonstrate working of // recursion #include <bits/stdc++.h> using namespace std;  void printFun(int test) {     if (test < 1)         return;     else {         cout << test << " ";         printFun(test - 1); // statement 2         cout << test << " ";         return;     } }  // Driver Code int main() {     int test = 3;     printFun(test); }

// A C program to demonstrate working of recursion #include <stdio.h>  void printFun(int test) {     if (test < 1)         return;     else {         printf("%d ", test);         printFun(test - 1); // statement 2         printf("%d ", test);         return;     } }  // Driver Code int main() {     int test = 3;     printFun(test);     return 0; }

Java

// A Java program to demonstrate working of // recursion class GFG {     static void printFun(int test)     {         if (test < 1)             return;         else {             System.out.printf("%d ", test);             printFun(test - 1); // statement 2             System.out.printf("%d ", test);             return;         }     }      // Driver Code     public static void main(String[] args)     {         int test = 3;         printFun(test);     } }  // This code is contributed by // Smitha Dinesh Semwal

Python

# A Python 3 program to # demonstrate working of # recursion   def printFun(test):      if (test < 1):         return     else:          print(test, end=" ")         printFun(test-1)  # statement 2         print(test, end=" ")         return  # Driver Code test = 3 printFun(test)  # This code is contributed by # Smitha Dinesh Semwal

// A C# program to demonstrate // working of recursion using System;  class GFG {      // function to demonstrate     // working of recursion     static void printFun(int test)     {         if (test < 1)             return;         else {             Console.Write(test + " ");              // statement 2             printFun(test - 1);              Console.Write(test + " ");             return;         }     }      // Driver Code     public static void Main(String[] args)     {         int test = 3;         printFun(test);     } }  // This code is contributed by Anshul Aggarwal.

JavaScript

// A JavaScript program to demonstrate working of recursion function printFun(test) {     if (test < 1)         return;     else {         console.log(test);         printFun(test - 1); // statement 2         console.log(test);         return;     } }  // Driver Code let test = 3; printFun(test);

PHP

<?php // PHP program to demonstrate  // working of recursion  // function to demonstrate  // working of recursion function printFun($test) {     if ($test < 1)         return;     else     {         echo("$test ");                  // statement 2         printFun($test-1);                   echo("$test ");         return;     } }  // Driver Code $test = 3; printFun($test);  // This code is contributed by // Smitha Dinesh Semwal. ?>

Output

3 2 1 1 2 3

Initial Call: When printFun(3) is called from main(), memory is allocated for printFun(3). The local variable test is initialized to 3, and statements 1 to 4 are pushed onto the stack.

First Recursive Call:

printFun(3) calls printFun(2).
Memory for printFun(2) is allocated, the local variable test is initialized to 2, and statements 1 to 4 are pushed onto the stack.

Second Recursive Call:

printFun(2) calls printFun(1).
Memory for printFun(1) is allocated, the local variable test is initialized to 1, and statements 1 to 4 are pushed onto the stack.

Third Recursive Call:

printFun(1) calls printFun(0).
Memory for printFun(0) is allocated, the local variable test is initialized to 0, and statements 1 to 4 are pushed onto the stack.

Base Case: When printFun(0) is called, it hits the base case (if statement) and returns control to printFun(1).

Returning from Recursion:

After returning from printFun(0), the remaining statements of printFun(1) are executed and it returns control to printFun(2).
Similarly, after returning from printFun(2), control returns to printFun(3).

Output: As a result, the output will print the values in the following order:

From 3 down to 1 (as the recursive calls are made).
Then from 1 back to 3 (as the recursive calls unwind).

The memory stack grows with each function call and shrinks as the recursion unwinds, following the LIFO structure.

Recursion VS Iteration

SR No.	Recursion	Iteration
1)	Terminates when the base case becomes true.	Terminates when the loop condition becomes false.
2)	Logic is built in terms of smaller problems.	Logic is built using iterating over something.
3)	Every recursive call needs extra space in the stack memory.	Every iteration does not require any extra space.
4)	Smaller code size.	Larger code size.

What are the advantages of recursive programming over iterative programming?

Recursion provides a clean and simple way to write code.
Some problems are inherently recursive like tree traversals, Tower of Hanoi, etc. For such problems, it is preferred to write recursive code. We can write such codes also iteratively with the help of a stack data structure. For example refer Inorder Tree Traversal without Recursion, Iterative Tower of Hanoi.

What are the disadvantages of recursive programming over iterative programming?

Note every recursive program can be written iteratively and vice versa is also true.

Recursive programs typically have more space requirements and also more time to maintain the recursion call stack.
Recursion can make the code more difficult to understand and debug, since it requires thinking about multiple levels of function calls..

Example 3 : Fibonacci with Recursion

Write a program and recurrence relation to find the Fibonacci series of n where n >= 0.

Mathematical Equation:

n if n == 0, n == 1;
fib(n) = fib(n-1) + fib(n-2) otherwise;

Recurrence Relation:

T(n) = T(n-1) + T(n-2) + O(1)

C++

// C++ code to implement Fibonacci series #include <bits/stdc++.h> using namespace std;  // Function for fibonacci  int fib(int n) {     // Stop condition     if (n == 0)         return 0;      // Stop condition     if (n == 1 || n == 2)         return 1;      // Recursion function     else         return (fib(n - 1) + fib(n - 2)); }  // Driver Code int main() {     // Initialize variable n.     int n = 5;     cout<<"Fibonacci series of 5 numbers is: ";      // for loop to print the fibonacci series.     for (int i = 0; i < n; i++)      {         cout<<fib(i)<<" ";     }     return 0; }

// C code to implement Fibonacci series #include <stdio.h>  // Function for fibonacci int fib(int n) {     // Stop condition     if (n == 0)         return 0;      // Stop condition     if (n == 1 || n == 2)         return 1;      // Recursion function     else         return (fib(n - 1) + fib(n - 2)); }  // Driver Code int main() {     // Initialize variable n.     int n = 5;     printf("Fibonacci series "            "of %d numbers is: ",            n);      // for loop to print the fibonacci series.     for (int i = 0; i < n; i++) {         printf("%d ", fib(i));     }     return 0; }

Java

// Java code to implement Fibonacci series import java.util.*;  class GFG {  // Function for fibonacci static int fib(int n) {     // Stop condition     if (n == 0)         return 0;      // Stop condition     if (n == 1 || n == 2)         return 1;      // Recursion function     else         return (fib(n - 1) + fib(n - 2)); }  // Driver Code public static void main(String []args) {        // Initialize variable n.     int n = 5;     System.out.print("Fibonacci series of 5 numbers is: ");      // for loop to print the fibonacci series.     for (int i = 0; i < n; i++)      {         System.out.print(fib(i)+" ");     } } }  // This code is contributed by rutvik_56.

Python

# Python code to implement Fibonacci series  # Function for fibonacci def fib(n):      # Stop condition     if (n == 0):         return 0      # Stop condition     if (n == 1 or n == 2):         return 1      # Recursion function     else:         return (fib(n - 1) + fib(n - 2))   # Driver Code  # Initialize variable n. n = 5; print("Fibonacci series of 5 numbers is :",end=" ")  # for loop to print the fibonacci series. for i in range(0,n):      print(fib(i),end=" ")

using System;  public class GFG {    // Function for fibonacci   static int fib(int n)   {      // Stop condition     if (n == 0)       return 0;      // Stop condition     if (n == 1 || n == 2)       return 1;      // Recursion function     else       return (fib(n - 1) + fib(n - 2));   }    // Driver Code   static public void Main ()   {      // Initialize variable n.     int n = 5;     Console.Write("Fibonacci series of 5 numbers is: ");      // for loop to print the fibonacci series.     for (int i = 0; i < n; i++)      {       Console.Write(fib(i) + " ");     }   } }  // This code is contributed by avanitrachhadiya2155

JavaScript

// Function for fibonacci function fib(n) {     // Stop condition     if (n === 0) return 0;      // Stop condition     if (n === 1 || n === 2) return 1;      // Recursion function     return fib(n - 1) + fib(n - 2); }  // Driver Code let n = 5; console.log("Fibonacci series of 5 numbers is:");  // for loop to print the fibonacci series. for (let i = 0; i < n; i++) {     console.log(fib(i) + " "); }

Output

Fibonacci series of 5 numbers is: 0 1 1 2 3

Recursion Tree for the above Code:

fibonacci series

Common Applications of Recursion

Tree and Graph Traversal: Used for systematically exploring nodes/vertices in data structures like trees and graphs.
Sorting Algorithms: Algorithms like quicksort and merge sort divide data into subarrays, sort them recursively, and merge them.
Divide-and-Conquer Algorithms: Algorithms like binary search break problems into smaller subproblems using recursion.
Fractal Generation: Recursion helps generate fractal patterns, such as the Mandelbrot set, by repeatedly applying a recursive formula.
Backtracking Algorithms: Used for problems requiring a sequence of decisions, where recursion explores all possible paths and backtracks when needed.
Memoization: Involves caching results of recursive function calls to avoid recomputing expensive subproblems.

These are just a few examples of the many applications of recursion in computer science and programming. Recursion is a versatile and powerful tool that can be used to solve many different types of problems.

Summary of Recursion:

There are two types of cases in recursion i.e. recursive case and a base case.
The base case is used to terminate the recursive function when the case turns out to be true.
Each recursive call makes a new copy of that method in the stack memory.
Infinite recursion may lead to running out of stack memory.
Examples of Recursive algorithms: Merge Sort, Quick Sort, Tower of Hanoi, Fibonacci Series, Factorial Problem, etc.