Breadth First Search or BFS for a Graph
Last Updated : 21 Apr, 2025
Given a undirected graph represented by an adjacency list adj, where each adj[i] represents the list of vertices connected to vertex i. Perform a Breadth First Search (BFS) traversal starting from vertex 0, visiting vertices from left to right according to the adjacency list, and return a list containing the BFS traversal of the graph.
Examples:
Input: adj[][] = [[1,2], [0,2,3], [0,1,4], [1,4], [2,3]]
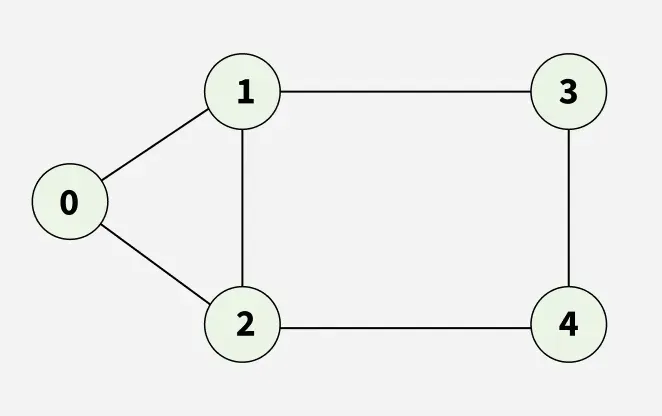
Output: [0, 1, 2, 3, 4]
Explanation: Starting from 0, the BFS traversal will follow these steps:
Visit 0 → Output: [0]
Visit 1 (first neighbor of 0) → Output: [0, 1]
Visit 2 (next neighbor of 0) → Output: [0, 1, 2]
Visit 3 (next neighbor of 1) → Output: [0, 1, 2, 3]
Visit 4 (neighbor of 2) → Final Output: [0, 1, 2, 3, 4]
Input: adj[][] = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]
 Output: [0, 1, 2, 3, 4]
Output: [0, 1, 2, 3, 4]
Explanation: Starting from 0, the BFS traversal proceeds as follows:
Visit 0 → Output: [0]
Visit 1 (the first neighbor of 0) → Output: [0, 1]
Visit 2 (the next neighbor of 0) → Output: [0, 1, 2]
Visit 3 (the first neighbor of 2 that hasn’t been visited yet) → Output: [0, 1, 2, 3]
Visit 4 (the next neighbor of 2) → Final Output: [0, 1, 2, 3, 4]
What is Breadth First Search?
Breadth First Search (BFS) is a fundamental graph traversal algorithm. It begins with a node, then first traverses all its adjacent nodes. Once all adjacent are visited, then their adjacent are traversed.
- BFS is different from DFS in a way that closest vertices are visited before others. We mainly traverse vertices level by level.
- Popular graph algorithms like Dijkstra’s shortest path, Kahn’s Algorithm, and Prim’s algorithm are based on BFS.
- BFS itself can be used to detect cycle in a directed and undirected graph, find shortest path in an unweighted graph and many more problems.
BFS from a Given Source
The algorithm starts from a given source and explores all reachable vertices from the given source. It is similar to the Breadth-First Traversal of a tree. Like tree, we begin with the given source (in tree, we begin with root) and traverse vertices level by level using a queue data structure. The only catch here is that, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a Boolean visited array.
Follow the below given approach:
- Initialization: Enqueue the given source vertex into a queue and mark it as visited.
- Exploration: While the queue is not empty:
- Dequeue a node from the queue and visit it (e.g., print its value).
- For each unvisited neighbor of the dequeued node:
- Enqueue the neighbor into the queue.
- Mark the neighbor as visited.
- Termination: Repeat step 2 until the queue is empty.
This algorithm ensures that all nodes in the graph are visited in a breadth-first manner, starting from the starting node.
C++ #include<bits/stdc++.h> using namespace std; // BFS from given source s vector<int> bfs(vector<vector<int>>& adj) { int V = adj.size(); int s = 0; // source node // create an array to store the traversal vector<int> res; // Create a queue for BFS queue<int> q; // Initially mark all the vertices as not visited vector<bool> visited(V, false); // Mark source node as visited and enqueue it visited[s] = true; q.push(s); // Iterate over the queue while (!q.empty()) { // Dequeue a vertex from queue and store it int curr = q.front(); q.pop(); res.push_back(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it for (int x : adj[curr]) { if (!visited[x]) { visited[x] = true; q.push(x); } } } return res; } int main() { vector<vector<int>> adj = {{1,2}, {0,2,3}, {0,4}, {1,4}, {2,3}}; vector<int> ans = bfs(adj); for(auto i:ans) { cout<<i<<" "; } return 0; } // Function to find BFS of Graph from given source s import java.util.*; class GfG { // BFS from given source s static ArrayList<Integer> bfs( ArrayList<ArrayList<Integer>> adj) { int V = adj.size(); int s = 0; // source node // create an array to store the traversal ArrayList<Integer> res = new ArrayList<>(); // Create a queue for BFS Queue<Integer> q = new LinkedList<>(); // Initially mark all the vertices as not visited boolean[] visited = new boolean[V]; // Mark source node as visited and enqueue it visited[s] = true; q.add(s); // Iterate over the queue while (!q.isEmpty()) { // Dequeue a vertex from queue and store it int curr = q.poll(); res.add(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it for (int x : adj.get(curr)) { if (!visited[x]) { visited[x] = true; q.add(x); } } } return res; } public static void main(String[] args) { // create the adjacency list // { {2, 3, 1}, {0}, {0, 4}, {0}, {2} } ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); adj.add(new ArrayList<>(Arrays.asList(1, 2))); adj.add(new ArrayList<>(Arrays.asList(0, 2, 3))); adj.add(new ArrayList<>(Arrays.asList(0, 4))); adj.add(new ArrayList<>(Arrays.asList(1,4))); adj.add(new ArrayList<>(Arrays.asList(2,3))); ArrayList<Integer> ans = bfs(adj); for (int i : ans) { System.out.print(i + " "); } } } # Function to find BFS of Graph from given source s def bfs(adj): # get number of vertices V = len(adj) # create an array to store the traversal res = [] s = 0 # Create a queue for BFS from collections import deque q = deque() # Initially mark all the vertices as not visited visited = [False] * V # Mark source node as visited and enqueue it visited[s] = True q.append(s) # Iterate over the queue while q: # Dequeue a vertex from queue and store it curr = q.popleft() res.append(curr) # Get all adjacent vertices of the dequeued # vertex curr If an adjacent has not been # visited, mark it visited and enqueue it for x in adj[curr]: if not visited[x]: visited[x] = True q.append(x) return res if __name__ == "__main__": # create the adjacency list # [ [2, 3, 1], [0], [0, 4], [0], [2] ] adj = [[1,2], [0,2,3], [0,4], [1,4], [2,3]] ans = bfs(adj) for i in ans: print(i, end=" ")
// Function to find BFS of Graph from given source s using System; using System.Collections.Generic; class GfG { // BFS from given source s static List<int> bfs(List<int>[] adj) { int V = adj.Length; int s = 0; // source node // create an array to store the traversal List<int> res = new List<int>(); // Create a queue for BFS Queue<int> q = new Queue<int>(); // Initially mark all the vertices as not visited bool[] visited = new bool[V]; // Mark source node as visited and enqueue it visited[s] = true; q.Enqueue(s); // Iterate over the queue while (q.Count > 0) { // Dequeue a vertex from queue and store it int curr = q.Dequeue(); res.Add(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it foreach (int x in adj[curr]) { if (!visited[x]) { visited[x] = true; q.Enqueue(x); } } } return res; } static void Main() { // create the adjacency list // { {2, 3, 1}, {0}, {0, 4}, {0}, {2} } List<int>[] adj = new List<int>[5]; adj[0] = new List<int> { 1, 2 }; adj[1] = new List<int> { 0, 2, 3 }; adj[2] = new List<int> { 0, 4 }; adj[3] = new List<int> { 1, 4 }; adj[4] = new List<int> { 2, 3 }; List<int> ans = bfs(adj); foreach (int i in ans) { Console.Write(i + " "); } } } // Function to find BFS of Graph from given source s function bfs(adj) { let V = adj.length; let s = 0; // source node is 0 // create an array to store the traversal let res = []; // Create a queue for BFS let q = []; // Initially mark all the vertices as not visited let visited = new Array(V).fill(false); // Mark source node as visited and enqueue it visited[s] = true; q.push(s); // Iterate over the queue while (q.length > 0) { // Dequeue a vertex from queue and store it let curr = q.shift(); res.push(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it for (let x of adj[curr]) { if (!visited[x]) { visited[x] = true; q.push(x); } } } return res; } // Main execution let adj = [ [1,2], [0,2,3], [0,4], [1,4], [2,3]]; let src = 0; let ans = bfs(adj); for (let i of ans) { process.stdout.write(i + " "); } BFS of the Disconnected Graph
The above implementation takes a source as an input and prints only those vertices that are reachable from the source and would not print all vertices in case of disconnected graph. Let us see the algorithm that prints all vertices without any source and the graph maybe disconnected.
The algorithm is simple, instead of calling BFS for a single vertex, we call the above implemented BFS for all not yet visited vertices one by one.
C++ #include<bits/stdc++.h> using namespace std; // BFS from given source s void bfs(vector<vector<int>>& adj, int s, vector<bool>& visited, vector<int> &res) { // Create a queue for BFS queue<int> q; // Mark source node as visited and enqueue it visited[s] = true; q.push(s); // Iterate over the queue while (!q.empty()) { // Dequeue a vertex and store it int curr = q.front(); q.pop(); res.push_back(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it for (int x : adj[curr]) { if (!visited[x]) { visited[x] = true; q.push(x); } } } } // Perform BFS for the entire graph which maybe // disconnected vector<int> bfsDisconnected(vector<vector<int>>& adj) { int V = adj.size(); // create an array to store the traversal vector<int> res; // Initially mark all the vertices as not visited vector<bool> visited(V, false); // perform BFS for each node for (int i = 0; i < adj.size(); ++i) { if (!visited[i]) { bfs(adj, i, visited, res); } } return res; } int main() { vector<vector<int>> adj = { {1, 2}, {0}, {0}, {4}, {3, 5}, {4}}; vector<int> ans = bfsDisconnected(adj); for(auto i:ans) { cout<<i<<" "; } return 0; } // BFS from given source s import java.util.*; class GfG { // BFS from given source s static ArrayList<Integer> bfsOfGraph(ArrayList<ArrayList<Integer>> adj, int s, boolean[] visited, ArrayList<Integer> res) { // Create a queue for BFS Queue<Integer> q = new LinkedList<>(); // Mark source node as visited and enqueue it visited[s] = true; q.add(s); // Iterate over the queue while (!q.isEmpty()) { // Dequeue a vertex and store it int curr = q.poll(); res.add(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it for (int x : adj.get(curr)) { if (!visited[x]) { visited[x] = true; q.add(x); } } } return res; } // Perform BFS for the entire graph which maybe // disconnected static ArrayList<Integer> bfsDisconnected( ArrayList<ArrayList<Integer>> adj) { int V = adj.size(); // create an array to store the traversal ArrayList<Integer> res = new ArrayList<>(); // Initially mark all the vertices as not visited boolean[] visited = new boolean[V]; // perform BFS for each node for (int i = 0; i < V; i++) { if (!visited[i]) { bfsOfGraph(adj, i, visited, res); } } return res; } public static void main(String[] args) { ArrayList<ArrayList<Integer>> adj = new ArrayList<>(); adj.add(new ArrayList<>(Arrays.asList(1, 2))); adj.add(new ArrayList<>(Arrays.asList(0))); adj.add(new ArrayList<>(Arrays.asList(0))); adj.add(new ArrayList<>(Arrays.asList(4))); adj.add(new ArrayList<>(Arrays.asList(3, 5))); adj.add(new ArrayList<>(Arrays.asList(4))); int src = 0; ArrayList<Integer> ans = bfsDisconnected(adj); for (int i : ans) { System.out.print(i + " "); } } } # BFS from given source s from collections import deque def bfsOfGraph(adj, s, visited, res): # Create a queue for BFS q = deque() # Mark source node as visited and enqueue it visited[s] = True q.append(s) # Iterate over the queue while q: # Dequeue a vertex and store it curr = q.popleft() res.append(curr) # Get all adjacent vertices of the dequeued # vertex curr If an adjacent has not been # visited, mark it visited and enqueue it for x in adj[curr]: if not visited[x]: visited[x] = True q.append(x) return res # Perform BFS for the entire graph which maybe # disconnected def bfsDisconnected(adj): V = len(adj) # create an array to store the traversal res = [] # Initially mark all the vertices as not visited visited = [False] * V # perform BFS for each node for i in range(V): if not visited[i]: bfsOfGraph(adj, i, visited, res) return res if __name__ == "__main__": adj = [[1, 2], [0], [0], [4], [3, 5], [4]] ans = bfsDisconnected(adj) for i in ans: print(i, end=" ")
// BFS from given source s using System; using System.Collections.Generic; class GfG { // BFS from given source s static List<int> bfsOfGraph(List<int>[] adj, int s, bool[] visited, List<int> res) { // Create a queue for BFS Queue<int> q = new Queue<int>(); // Mark source node as visited and enqueue it visited[s] = true; q.Enqueue(s); // Iterate over the queue while (q.Count > 0) { // Dequeue a vertex and store it int curr = q.Dequeue(); res.Add(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it foreach (int x in adj[curr]) { if (!visited[x]) { visited[x] = true; q.Enqueue(x); } } } return res; } // Perform BFS for the entire graph which maybe // disconnected static List<int> bfsDisconnected(List<int>[] adj) { int V = adj.Length; // create an array to store the traversal List<int> res = new List<int>(); // Initially mark all the vertices as not visited bool[] visited = new bool[V]; // perform BFS for each node for (int i = 0; i < V; i++) { if (!visited[i]) { bfsOfGraph(adj, i, visited, res); } } return res; } static void Main() { List<int>[] adj = new List<int>[6]; adj[0] = new List<int> { 1, 2 }; adj[1] = new List<int> { 0 }; adj[2] = new List<int> { 0 }; adj[3] = new List<int> { 4 }; adj[4] = new List<int> { 3, 5 }; adj[5] = new List<int> { 4 }; List<int> ans = bfsDisconnected(adj); foreach (int i in ans) { Console.Write(i + " "); } } } // BFS from given source s function bfsOfGraph(adj, s, visited, res) { // Create a queue for BFS let q = []; // Mark source node as visited and enqueue it visited[s] = true; q.push(s); // Iterate over the queue while (q.length > 0) { // Dequeue a vertex and store it let curr = q.shift(); res.push(curr); // Get all adjacent vertices of the dequeued // vertex curr If an adjacent has not been // visited, mark it visited and enqueue it for (let x of adj[curr]) { if (!visited[x]) { visited[x] = true; q.push(x); } } } return res; } // Perform BFS for the entire graph which maybe // disconnected function bfsDisconnected(adj) { let V = adj.length; // create an array to store the traversal let res = []; // Initially mark all the vertices as not visited let visited = new Array(V).fill(false); // perform BFS for each node for (let i = 0; i < V; i++) { if (!visited[i]) { bfsOfGraph(adj, i, visited, res); } } return res; } // Main execution let adj = [[1, 2], [0], [0], [4], [3, 5], [4]]; let ans = bfsDisconnected(adj); for (let i of ans) { process.stdout.write(i + " "); } Complexity Analysis of Breadth-First Search (BFS) Algorithm
Time Complexity: O(V + E), BFS explores all the vertices and edges in the graph. In the worst case, it visits every vertex and edge once. Therefore, the time complexity of BFS is O(V + E), where V and E are the number of vertices and edges in the given graph.
Auxiliary Space: O(V), BFS uses a queue to keep track of the vertices that need to be visited. In the worst case, the queue can contain all the vertices in the graph. Therefore, the space complexity of BFS is O(V).
Applications of BFS in Graphs
BFS has various applications in graph theory and computer science, including:
- Shortest Path Finding: BFS can be used to find the shortest path between two nodes in an unweighted graph. By keeping track of the parent of each node during the traversal, the shortest path can be reconstructed.
- Cycle Detection: BFS can be used to detect cycles in a graph. If a node is visited twice during the traversal, it indicates the presence of a cycle.
- Connected Components: BFS can be used to identify connected components in a graph. Each connected component is a set of nodes that can be reached from each other.
- Topological Sorting: BFS can be used to perform topological sorting on a directed acyclic graph (DAG). Topological sorting arranges the nodes in a linear order such that for any edge (u, v), u appears before v in the order.
- Level Order Traversal of Binary Trees: BFS can be used to perform a level order traversal of a binary tree. This traversal visits all nodes at the same level before moving to the next level.
- Network Routing: BFS can be used to find the shortest path between two nodes in a network, making it useful for routing data packets in network protocols.
Problems on BFS for a Graph
FAQs on Breadth First Search (BFS) for a Graph
Question 1: What is BFS and how does it work?
Answer: BFS is a graph traversal algorithm that systematically explores a graph by visiting all the vertices at a given level before moving on to the next level. It starts from a starting vertex, enqueues it into a queue, and marks it as visited. Then, it dequeues a vertex from the queue, visits it, and enqueues all its unvisited neighbors into the queue. This process continues until the queue is empty.
Question 2: What are the applications of BFS?
Answer: BFS has various applications, including finding the shortest path in an unweighted graph, detecting cycles in a graph, topologically sorting a directed acyclic graph (DAG), finding connected components in a graph, and solving puzzles like mazes and Sudoku.
Question 3: What is the time complexity of BFS?
Answer: The time complexity of BFS is O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Question 4: What is the space complexity of BFS?
Answer: The space complexity of BFS is O(V), as it uses a queue to keep track of the vertices that need to be visited.
Question 5: What are the advantages of using BFS?
Answer: BFS is simple to implement and efficient for finding the shortest path in an unweighted graph. It also guarantees that all the vertices in the graph are visited.
Related Articles:
Similar Reads
Breadth First Search or BFS for a Graph
Given a undirected graph represented by an adjacency list adj, where each adj[i] represents the list of vertices connected to vertex i. Perform a Breadth First Search (BFS) traversal starting from vertex 0, visiting vertices from left to right according to the adjacency list, and return a list conta
15+ min read
BFS in different language
BFS for Disconnected Graph
In the previous post, BFS only with a particular vertex is performed i.e. it is assumed that all vertices are reachable from the starting vertex. But in the case of a disconnected graph or any vertex that is unreachable from all vertex, the previous implementation will not give the desired output, s
14 min read
Applications, Advantages and Disadvantages of Breadth First Search (BFS)
We have earlier discussed Breadth First Traversal Algorithm for Graphs. Here in this article, we will see the applications, advantages, and disadvantages of the Breadth First Search. Applications of Breadth First Search: 1. Shortest Path and Minimum Spanning Tree for unweighted graph: In an unweight
4 min read
Breadth First Traversal ( BFS ) on a 2D array
Given a matrix of size M x N consisting of integers, the task is to print the matrix elements using Breadth-First Search traversal. Examples: Input: grid[][] = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}}Output: 1 2 5 3 6 9 4 7 10 13 8 11 14 12 15 16 Input: grid[][] = {{-1, 0, 0,
9 min read
0-1 BFS (Shortest Path in a Binary Weight Graph)
Given a graph where every edge has weight as either 0 or 1. A source vertex is also given in the graph. Find the shortest path from the source vertex to every other vertex. For Example: Input : Source Vertex = 0 and below graph Having vertices like(u,v,w): Edges: [[0,1,0], [0, 7, 1], [1,2,1], [1,
9 min read
Variations of BFS implementations
Easy problems on BFS
Find if there is a path between two vertices in a directed graph
Given a Directed Graph and two vertices in it, check whether there is a path from the first given vertex to second. Example: Consider the following Graph: Input : (u, v) = (1, 3) Output: Yes Explanation: There is a path from 1 to 3, 1 -> 2 -> 3 Input : (u, v) = (3, 6) Output: No Explanation: T
15 min read
Find if there is a path between two vertices in an undirected graph
Given an undirected graph with N vertices and E edges and two vertices (U, V) from the graph, the task is to detect if a path exists between these two vertices. Print "Yes" if a path exists and "No" otherwise. Examples: U = 1, V = 2 Output: No Explanation: There is no edge between the two points and
15+ min read
Print all the levels with odd and even number of nodes in it | Set-2
Given an N-ary tree, print all the levels with odd and even number of nodes in it. Examples: For example consider the following tree 1 - Level 1 / \ 2 3 - Level 2 / \ \ 4 5 6 - Level 3 / \ / 7 8 9 - Level 4 The levels with odd number of nodes are: 1 3 4 The levels with even number of nodes are: 2 No
12 min read
Finding the path from one vertex to rest using BFS
Given an adjacency list representation of a directed graph, the task is to find the path from source to every other node in the graph using BFS. Examples: Input: Output: 0 <- 2 1 <- 0 <- 2 2 3 <- 1 <- 0 <- 2 4 <- 5 <- 2 5 <- 2 6 <- 2 Approach: In the images shown below:
14 min read
Find all reachable nodes from every node present in a given set
Given an undirected graph and a set of vertices, find all reachable nodes from every vertex present in the given set. Consider below undirected graph with 2 disconnected components.  arr[] = {1 , 2 , 5}Reachable nodes from 1 are 1, 2, 3, 4Reachable nodes from 2 are 1, 2, 3, 4Reachable nodes from 5
12 min read
Program to print all the non-reachable nodes | Using BFS
Given an undirected graph and a set of vertices, we have to print all the non-reachable nodes from the given head node using a breadth-first search. For example: Consider below undirected graph with two disconnected components: In this graph, if we consider 0 as a head node, then the node 0, 1 and 2
8 min read
Check whether a given graph is Bipartite or not
Given a graph with V vertices numbered from 0 to V-1 and a list of edges, determine whether the graph is bipartite or not. Note: A bipartite graph is a type of graph where the set of vertices can be divided into two disjoint sets, say U and V, such that every edge connects a vertex in U to a vertex
9 min read
Print all paths from a given source to a destination using BFS
Given a directed graph, a source vertex ‘src’ and a destination vertex ‘dst’, print all paths from given ‘src’ to ‘dst’. Please note that in the cases, we have cycles in the graph, we need not to consider paths have cycles as in case of cycles, there can by infinitely many by doing multiple iteratio
9 min read
Minimum steps to reach target by a Knight | Set 1
Given a square chessboard of n x n size, the position of the Knight and the position of a target are given. We need to find out the minimum steps a Knight will take to reach the target position. Examples: Input: knightPosition: (1, 3) , targetPosition: (5, 0) Output: 3Explanation: In above diagram K
9 min read
Intermediate problems on BFS
Traversal of a Graph in lexicographical order using BFS
C/C++ Code // C++ program to implement // the above approach #include <bits/stdc++.h> using namespace std; // Function to traverse the graph in // lexicographical order using BFS void LexiBFS(map<char, set<char> >& G, char S, map<char, bool>& vis) { // Stores nodes of
9 min read
Detect cycle in an undirected graph using BFS
Given an undirected graph, the task is to determine if cycle is present in it or not. Examples: Input: V = 5, edges[][] = [[0, 1], [0, 2], [0, 3], [1, 2], [3, 4]] Output: trueExplanation: The diagram clearly shows a cycle 0 → 2 → 1 → 0. Input: V = 4, edges[][] = [[0, 1], [1, 2], [2, 3]] Output: fals
6 min read
Detect Cycle in a Directed Graph using BFS
Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false. For example, the following graph contains two cycles 0->1->2->3->0 and 2->4->2, so your function must return
11 min read
Minimum number of edges between two vertices of a Graph
You are given an undirected graph G(V, E) with N vertices and M edges. We need to find the minimum number of edges between a given pair of vertices (u, v). Examples: Input: For given graph G. Find minimum number of edges between (1, 5). Output: 2Explanation: (1, 2) and (2, 5) are the only edges resu
8 min read
Word Ladder - Shortest Chain To Reach Target Word
Given an array of strings arr[], and two different strings start and target, representing two words. The task is to find the length of the smallest chain from string start to target, such that only one character of the adjacent words differs and each word exists in arr[]. Note: Print 0 if it is not
15 min read
Print the lexicographically smallest BFS of the graph starting from 1
Given a connected graph with N vertices and M edges. The task is to print the lexicographically smallest BFS traversal of the graph starting from 1. Note: The vertices are numbered from 1 to N.Examples: Input: N = 5, M = 5 Edges: 1 4 3 4 5 4 3 2 1 5 Output: 1 4 3 2 5 Start from 1, go to 4, then to 3
7 min read
Shortest path in an unweighted graph
Given an unweighted, undirected graph of V nodes and E edges, a source node S, and a destination node D, we need to find the shortest path from node S to node D in the graph. Input: V = 8, E = 10, S = 0, D = 7, edges[][] = {{0, 1}, {1, 2}, {0, 3}, {3, 4}, {4, 7}, {3, 7}, {6, 7}, {4, 5}, {4, 6}, {5,
11 min read
Number of shortest paths in an unweighted and directed graph
Given an unweighted directed graph, can be cyclic or acyclic. Print the number of shortest paths from a given vertex to each of the vertices. For example consider the below graph. There is one shortest path vertex 0 to vertex 0 (from each vertex there is a single shortest path to itself), one shorte
11 min read
Distance of nearest cell having 1 in a binary matrix
Given a binary grid of n*m. Find the distance of the nearest 1 in the grid for each cell.The distance is calculated as |i1 - i2| + |j1 - j2|, where i1, j1 are the row number and column number of the current cell, and i2, j2 are the row number and column number of the nearest cell having value 1. Th
15+ min read
Hard Problems on BFS
Islands in a graph using BFS
Given an n x m grid of 'W' (Water) and 'L' (Land), the task is to count the number of islands. An island is a group of adjacent 'L' cells connected horizontally, vertically, or diagonally, and it is surrounded by water or the grid boundary. The goal is to determine how many distinct islands exist in
15+ min read
Print all shortest paths between given source and destination in an undirected graph
Given an undirected and unweighted graph and two nodes as source and destination, the task is to print all the paths of the shortest length between the given source and destination.Examples: Input: source = 0, destination = 5 Output: 0 -> 1 -> 3 -> 50 -> 2 -> 3 -> 50 -> 1 ->
13 min read
Count Number of Ways to Reach Destination in a Maze using BFS
Given a maze of dimensions n x m represented by the matrix mat, where mat[i][j] = -1 represents a blocked cell and mat[i][j] = 0 represents an unblocked cell, the task is to count the number of ways to reach the bottom-right cell starting from the top-left cell by moving right (i, j+1) or down (i+1,
8 min read
Coin Change | BFS Approach
Given an integer X and an array arr[] of length N consisting of positive integers, the task is to pick minimum number of integers from the array such that they sum up to N. Any number can be chosen infinite number of times. If no answer exists then print -1.Examples: Input: X = 7, arr[] = {3, 5, 4}
6 min read
Water Jug problem using BFS
Given two empty jugs of m and n litres respectively. The jugs don't have markings to allow measuring smaller quantities. You have to use the jugs to measure d litres of water. The task is to find the minimum number of operations to be performed to obtain d litres of water in one of the jugs. In case
12 min read
Word Ladder - Set 2 ( Bi-directional BFS )
Given a dictionary, and two words start and target (both of the same length). Find length of the smallest chain from start to target if it exists, such that adjacent words in the chain only differ by one character and each word in the chain is a valid word i.e., it exists in the dictionary. It may b
15+ min read
Implementing Water Supply Problem using Breadth First Search
Given N cities that are connected using N-1 roads. Between Cities [i, i+1], there exists an edge for all i from 1 to N-1.The task is to set up a connection for water supply. Set the water supply in one city and water gets transported from it to other cities using road transport. Certain cities are b
10 min read
Minimum Cost Path in a directed graph via given set of intermediate nodes
Given a weighted, directed graph G, an array V[] consisting of vertices, the task is to find the Minimum Cost Path passing through all the vertices of the set V, from a given source S to a destination D. Examples: Input: V = {7}, S = 0, D = 6 Output: 11 Explanation: Minimum path 0->7->5->6.
10 min read
Shortest path in a Binary Maze
Given an M x N matrix where each element can either be 0 or 1. We need to find the shortest path between a given source cell to a destination cell. The path can only be created out of a cell if its value is 1. Note: You can move into an adjacent cell in one of the four directions, Up, Down, Left, an
15+ min read
Minimum cost to traverse from one index to another in the String
Given a string S of length N consisting of lower case character, the task is to find the minimum cost to reach from index i to index j. At any index k, the cost to jump to the index k+1 and k-1(without going out of bounds) is 1. Additionally, the cost to jump to any index m such that S[m] = S[k] is
10 min read